Verilog (3) – 組合邏輯電路 (作者：陳鍾誠)

Verilog (3) – 組合邏輯電路 (作者：陳鍾誠)

在數位電路當中，邏輯電路通常被分為兩類，一類是沒有「回饋線路」(No feedback) 的組合邏輯電路 (Combinatorial Logic)，另一類是有「回饋線路」的循序邏輯電路 (Sequential Logic)。

組合邏輯的線路只是將輸入訊號轉換成輸出訊號，像是加法器、多工器等都是組合邏輯電路的範例，由於中間不會暫存，因此無法記憶位元。而循序邏輯由於有回饋線路，所以可以製作出像 Flip-Flop，Latch 等記憶單元，可以記憶位元。

在本文中，我們將先專注在組合邏輯上，看看如何用基本的閘級寫法，寫出像多工器、加法器、減法器等組成 CPU 的基礎電路元件。

多工器

如果您曾經用硬接線的方式設計過 CPU，那就會發現「控制單元」主要就是一堆多工器的連接。多工器可以從很多組輸入資料中選擇一組輸出，以下是一個四選一多工器的方塊圖。

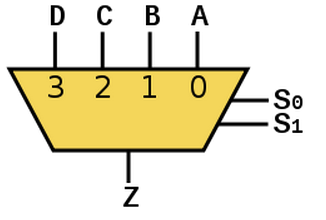
圖、4 選 1 多工器

4 選 1 多工器的內部電路結構如下：

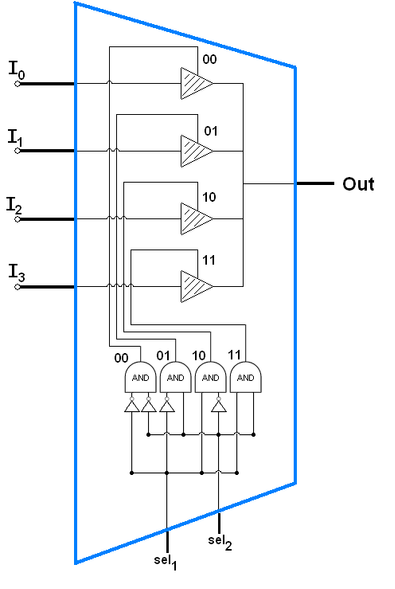
圖、4 選 1 多工器的內部電路

接著、就讓我們來看一個完整的 Verilog 的 4 選 1 的多工器程式，由於 Verilog 支援像 Case 這樣的高階語法，因此在實作時可以不需要採用細部的接線方式，只要使用 case 語句就可以輕易完成多工器的設計。

檔案：mux4.v

module mux4(input[1:0]  select, input[3:0] d, output reg q );
always @( select or d )
begin
   case( select )
       0 : q = d[0];
       1 : q = d[1];
       2 : q = d[2];
       3 : q = d[3];
   endcase
end
endmodule

module main;
reg [3:0] d;
reg [1:0] s;
wire q;

mux4 DUT (s, d, q);

initial
begin
  s = 0;
  d = 4'b0110;
end

always #50 begin
  s=s+1;
  $monitor("%4dns monitor: s=%d d=%d q=%d", $stime, s, d, q);
end

initial #1000 $finish;

endmodule

執行結果

D:\ccc101\icarus>iverilog mux4.v -o mux4

D:\ccc101\icarus>vvp mux4
  50ns monitor: s=1 d= 6 q=1
 100ns monitor: s=2 d= 6 q=1
 150ns monitor: s=3 d= 6 q=0
 200ns monitor: s=0 d= 6 q=0
 250ns monitor: s=1 d= 6 q=1
 300ns monitor: s=2 d= 6 q=1
 350ns monitor: s=3 d= 6 q=0
 400ns monitor: s=0 d= 6 q=0
 450ns monitor: s=1 d= 6 q=1
 500ns monitor: s=2 d= 6 q=1
 550ns monitor: s=3 d= 6 q=0
 600ns monitor: s=0 d= 6 q=0
 650ns monitor: s=1 d= 6 q=1
 700ns monitor: s=2 d= 6 q=1
 750ns monitor: s=3 d= 6 q=0
 800ns monitor: s=0 d= 6 q=0
 850ns monitor: s=1 d= 6 q=1
 900ns monitor: s=2 d= 6 q=1
 950ns monitor: s=3 d= 6 q=0
1000ns monitor: s=0 d= 6 q=0

您可以看到在上述範例中，輸入資料 6 的二進位是 0110，如下所示：

       位置 s  3 2 1 0
       位元 d  0 1 1 0

因此當 s=0 時會輸出 0, s=1 時會輸出 1, s=2 時會輸出 1, s=3 時會輸出 0，這就是上述輸出結果的意義。

加法器

接著、讓我們用先前已經示範過的全加器範例，一個一個連接成四位元的加法器，電路圖如下所示

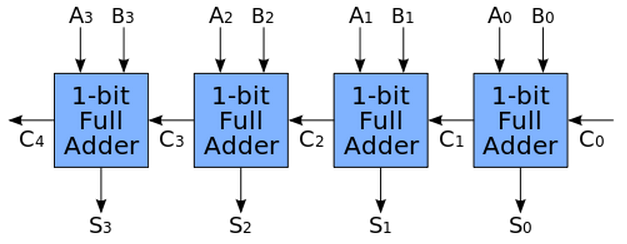
圖、用 4 個全加器組成 4 位元加法器

上圖寫成 Verilog 就變成以下 adder4 模組的程式內容。

module adder4(input signed [3:0] a, input signed [3:0] b, input c_in, output signed [3:0] sum, output c_out);
wire [3:0] c;

fulladder fa1(a[0],b[0], c_in, sum[0], c[1]) ;
fulladder fa2(a[1],b[1], c[1], sum[1], c[2]) ;
fulladder fa3(a[2],b[2], c[2], sum[2], c[3]) ;
fulladder fa4(a[3],b[3], c[3], sum[3], c_out) ;

endmodule

以下是完整的 4 位元加法器之 Verilog 程式。

檔案：adder4.v

module fulladder (input a, b, c_in, output sum, c_out);
wire s1, c1, c2;

xor g1(s1, a, b);
xor g2(sum, s1, c_in);
and g3(c1, a,b);
and g4(c2, s1, c_in) ;
xor g5(c_out, c2, c1) ;

endmodule

module adder4(input signed [3:0] a, input signed [3:0] b, input c_in, output signed [3:0] sum, output c_out);
wire [3:0] c;

fulladder fa1(a[0],b[0], c_in, sum[0], c[1]) ;
fulladder fa2(a[1],b[1], c[1], sum[1], c[2]) ;
fulladder fa3(a[2],b[2], c[2], sum[2], c[3]) ;
fulladder fa4(a[3],b[3], c[3], sum[3], c_out) ;

endmodule

module main;
reg signed [3:0] a;
reg signed [3:0] b;
wire signed [3:0] sum;
wire c_out;

adder4 DUT (a, b, 1'b0, sum, c_out);

initial
begin
  a = 4'b0101;
  b = 4'b0000;
end

always #50 begin
  b=b+1;
  $monitor("%dns monitor: a=%d b=%d sum=%d", $stime, a, b, sum);
end

initial #2000 $finish;

endmodule

執行結果

D:\ccc101\icarus\ccc>iverilog -o sadd4 sadd4.v

D:\ccc101\icarus\ccc>vvp sadd4
        50ns monitor: a= 5 b= 1 sum= 6
       100ns monitor: a= 5 b= 2 sum= 7
       150ns monitor: a= 5 b= 3 sum=-8
       200ns monitor: a= 5 b= 4 sum=-7
       250ns monitor: a= 5 b= 5 sum=-6
       300ns monitor: a= 5 b= 6 sum=-5
       350ns monitor: a= 5 b= 7 sum=-4
       400ns monitor: a= 5 b=-8 sum=-3
       450ns monitor: a= 5 b=-7 sum=-2
       500ns monitor: a= 5 b=-6 sum=-1
       550ns monitor: a= 5 b=-5 sum= 0
       600ns monitor: a= 5 b=-4 sum= 1
       650ns monitor: a= 5 b=-3 sum= 2
       700ns monitor: a= 5 b=-2 sum= 3
       750ns monitor: a= 5 b=-1 sum= 4
       800ns monitor: a= 5 b= 0 sum= 5
       850ns monitor: a= 5 b= 1 sum= 6
       900ns monitor: a= 5 b= 2 sum= 7
       950ns monitor: a= 5 b= 3 sum=-8
      1000ns monitor: a= 5 b= 4 sum=-7
      1050ns monitor: a= 5 b= 5 sum=-6
      1100ns monitor: a= 5 b= 6 sum=-5
      1150ns monitor: a= 5 b= 7 sum=-4
      1200ns monitor: a= 5 b=-8 sum=-3
      1250ns monitor: a= 5 b=-7 sum=-2
      1300ns monitor: a= 5 b=-6 sum=-1
      1350ns monitor: a= 5 b=-5 sum= 0
      1400ns monitor: a= 5 b=-4 sum= 1
      1450ns monitor: a= 5 b=-3 sum= 2
      1500ns monitor: a= 5 b=-2 sum= 3
      1550ns monitor: a= 5 b=-1 sum= 4
      1600ns monitor: a= 5 b= 0 sum= 5
      1650ns monitor: a= 5 b= 1 sum= 6
      1700ns monitor: a= 5 b= 2 sum= 7
      1750ns monitor: a= 5 b= 3 sum=-8
      1800ns monitor: a= 5 b= 4 sum=-7
      1850ns monitor: a= 5 b= 5 sum=-6
      1900ns monitor: a= 5 b= 6 sum=-5
      1950ns monitor: a= 5 b= 7 sum=-4
      2000ns monitor: a= 5 b=-8 sum=-3

在上述執行結果中，您可以看到在沒有溢位的情況下，sum = a+b，但是一但加總值超過 7 之後，那就會變成負值，這也正是有號二補數表示法溢位時會產生的結果。

加減器

接著、我們只要把上面的加法器，加上一組控制的互斥或閘，並控制輸入進位與否，就可以成為加減器了，這是因為我們採用了二補數的關係。

二補數讓我們可以很容易的延伸加法器電路就能做出減法器。我們可以在運算元 B 之前加上 2 選 1 多工器或 XOR 閘來控制 B 是否應該取補數，並且運用 OP 控制線路來進行控制，以下是採用 2 選 1 多工器的電路做法圖。

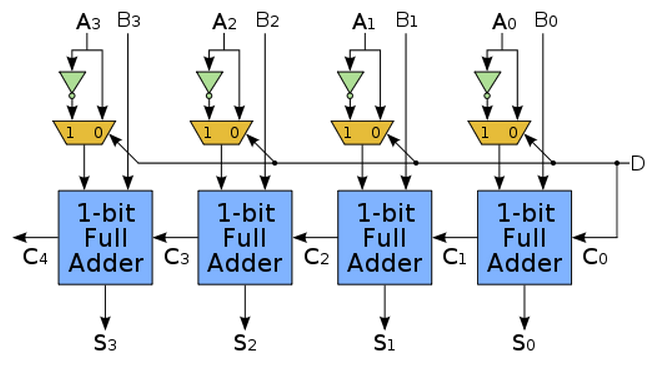
圖、採用 2 選 1 多工器控制的加減器電路

另一種更簡單的做法是採用 XOR 閘去控制 B 是否要取補數，如下圖所示：

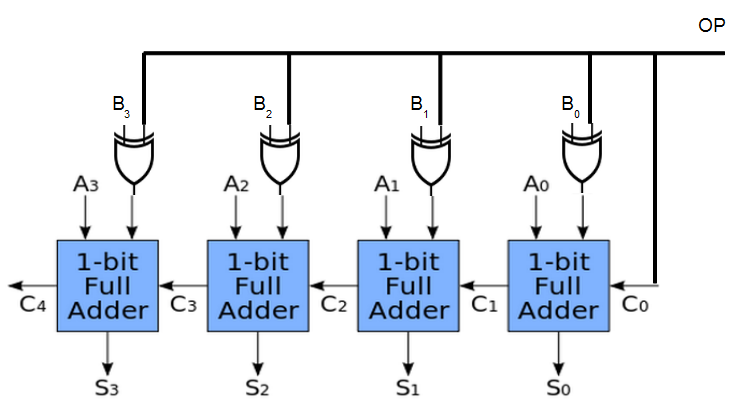
圖、採用 XOR 控制的加減器電路

清楚了電路圖的布局之後，讓我們來看看如何用 Verilog 實做加減器吧！關鍵部分的程式如下所示，這個模組就對應到上述的「採用 XOR 控制的加減器電路」之圖形。

module addSub4(input op, input signed [3:0] a, input signed [3:0] b, 
               output signed [3:0] sum, output c_out);

wire [3:0] bop;

xor4 x1(b, {op,op,op,op}, bop);
adder4 a1(a, bop, op, sum, c_out);

endmodule

接著讓我們來看看完整的加減器程式與測試結果。

檔案：addsub4.v

module fulladder (input a, b, c_in, output sum, c_out);
wire s1, c1, c2;

xor g1(s1, a, b);
xor g2(sum, s1, c_in);
and g3(c1, a,b);
and g4(c2, s1, c_in) ;
xor g5(c_out, c2, c1) ;

endmodule

module adder4(input signed [3:0] a, input signed [3:0] b, input c_in, 
              output signed [3:0] sum, output c_out);
wire [3:0] c;

fulladder fa1(a[0],b[0], c_in, sum[0], c[1]) ;
fulladder fa2(a[1],b[1], c[1], sum[1], c[2]) ;
fulladder fa3(a[2],b[2], c[2], sum[2], c[3]) ;
fulladder fa4(a[3],b[3], c[3], sum[3], c_out) ;

endmodule

module xor4(input [3:0] a, input [3:0] b, output [3:0] y);
  assign y = a ^ b;
endmodule

module addSub4(input op, input signed [3:0] a, input signed [3:0] b, 
               output signed [3:0] sum, output c_out);

wire [3:0] bop;

xor4 x1(b, {op,op,op,op}, bop);
adder4 a1(a, bop, op, sum, c_out);

endmodule

module main;
reg signed [3:0] a;
reg signed [3:0] b;
wire signed [3:0] sum;
reg op;
wire c_out;

addSub4 DUT (op, a, b, sum, c_out);

initial
begin
  a = 4'b0101;
  b = 4'b0000;
  op = 1'b0;
end

always #50 begin
  op=op+1;
  $monitor("%dns monitor: op=%d a=%d b=%d sum=%d", $stime, op, a, b, sum);
end

always #100 begin
  b=b+1;
end

initial #2000 $finish;

endmodule

執行結果：

D:\ccc101\icarus\ccc>iverilog -o addSub4 addSub4.v

D:\ccc101\icarus\ccc>vvp addSub4
        50ns monitor: op=1 a= 5 b= 0 sum= 5
       100ns monitor: op=0 a= 5 b= 1 sum= 6
       150ns monitor: op=1 a= 5 b= 1 sum= 4
       200ns monitor: op=0 a= 5 b= 2 sum= 7
       250ns monitor: op=1 a= 5 b= 2 sum= 3
       300ns monitor: op=0 a= 5 b= 3 sum=-8
       350ns monitor: op=1 a= 5 b= 3 sum= 2
       400ns monitor: op=0 a= 5 b= 4 sum=-7
       450ns monitor: op=1 a= 5 b= 4 sum= 1
       500ns monitor: op=0 a= 5 b= 5 sum=-6
       550ns monitor: op=1 a= 5 b= 5 sum= 0
       600ns monitor: op=0 a= 5 b= 6 sum=-5
       650ns monitor: op=1 a= 5 b= 6 sum=-1
       700ns monitor: op=0 a= 5 b= 7 sum=-4
       750ns monitor: op=1 a= 5 b= 7 sum=-2
       800ns monitor: op=0 a= 5 b=-8 sum=-3
       850ns monitor: op=1 a= 5 b=-8 sum=-3
       900ns monitor: op=0 a= 5 b=-7 sum=-2
       950ns monitor: op=1 a= 5 b=-7 sum=-4
      1000ns monitor: op=0 a= 5 b=-6 sum=-1
      1050ns monitor: op=1 a= 5 b=-6 sum=-5
      1100ns monitor: op=0 a= 5 b=-5 sum= 0
      1150ns monitor: op=1 a= 5 b=-5 sum=-6
      1200ns monitor: op=0 a= 5 b=-4 sum= 1
      1250ns monitor: op=1 a= 5 b=-4 sum=-7
      1300ns monitor: op=0 a= 5 b=-3 sum= 2
      1350ns monitor: op=1 a= 5 b=-3 sum=-8
      1400ns monitor: op=0 a= 5 b=-2 sum= 3
      1450ns monitor: op=1 a= 5 b=-2 sum= 7
      1500ns monitor: op=0 a= 5 b=-1 sum= 4
      1550ns monitor: op=1 a= 5 b=-1 sum= 6
      1600ns monitor: op=0 a= 5 b= 0 sum= 5
      1650ns monitor: op=1 a= 5 b= 0 sum= 5
      1700ns monitor: op=0 a= 5 b= 1 sum= 6
      1750ns monitor: op=1 a= 5 b= 1 sum= 4
      1800ns monitor: op=0 a= 5 b= 2 sum= 7
      1850ns monitor: op=1 a= 5 b= 2 sum= 3
      1900ns monitor: op=0 a= 5 b= 3 sum=-8
      1950ns monitor: op=1 a= 5 b= 3 sum= 2
      2000ns monitor: op=0 a= 5 b= 4 sum=-7

在上述結果中，您可以看到當 op=0 時，電路所作的是加法運算，例如：200ns monitor: op=0 a= 5 b= 2 sum= 7。而當 op=1 時，電路所做的是減法運算，例如：250ns monitor: op=1 a= 5 b= 2 sum= 3。

在本文中，我們大致將 CPU 設計當中最重要的組合邏輯電路，也就是「多工器、加法器與減法器」的設計原理說明完畢了，希望透過 Verilog 的實作方式，能讓讀者更瞭解數位電路的設計原理，並且為接下來所要介紹的「開放電腦計畫」進行鋪路的工作，以便讓讀者能夠具備用 Verilog 設計 CPU 的基礎，這樣在後續幾期的開放電腦計畫文章中，讀者才比較容易讀懂 CPU 的 Verilog 程式之設計原理。

參考文獻

【本文由陳鍾誠取材 (主要為圖片) 並修改自維基百科】

程式人雜誌 _{-- 2013 年 9 月號 (開放公益出版品)}

Verilog (3) – 組合邏輯電路 (作者：陳鍾誠)

多工器

加法器

加減器

結語

參考文獻

程式人雜誌 -- 2013 年 9 月號 (開放公益出版品)

Verilog (3) – 組合邏輯電路 (作者：陳鍾誠)

多工器

加法器

加減器

結語

參考文獻

程式人雜誌 _{-- 2013 年 9 月號 (開放公益出版品)}