R 統計軟體(7) – 主成分分析與因子分析 (作者：陳鍾誠)
簡介
雖然「主成分分析」(Principle Component Analysis) 通常出現在機率統計的課本當中，但事實上要理解這個技術 的核心數學知識，卻是線性代數。
學過線性代數的朋友們通常會知道一個很重要但卻又難以理解的抽象概念，那就是「特徵值」與「特徵向量」， 其數學算式如下：
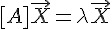
符合這種條件的的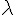 
就稱為特徵值，而 
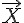則稱為特徵向量。
表面上來看，所謂的特徵向量 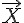就是矩陣 [A] 乘法運算上的一個方向不動點，乘完之後只會在該向量上進行常數倍的縮放，但方向不變。
不過、一個 n*n 矩陣的「特徵值」與「特徵向量」不止有一個，最大可以到達 n 個，假如共有 k 個特徵值，那我們可以列出下列運算式。
...
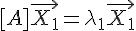
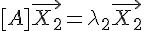
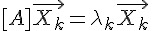
基本上、特徵值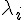 
越大的，代表該特徵向量越能用來描述整個矩陣 (或者說越能代表該矩陣)，所以如果我們只用特徵值最大的幾個 代表整個矩陣，將特徵值小的去除，基本上不會對整個矩陣造成太大的失真。
或許這樣講也不太精確，不過如果您還記得線性代數裏的 Rank 這個慨念，假如一個 3*3 矩陣的 rank 只有 2，那麼就代表三行當中，有一行可以用 其他兩行的線性組合取代，也就是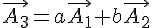 
。
在這種情況下，該矩陣只會有兩個不為零的特徵值 (也就是有一個特徵值為 0)，因此我們可以用兩組特徵值與特徵向量，就重建出整個矩陣。
而所謂的主成分，就是那些對重建矩陣有強大影響力，特徵值較大的那些向量。而那些特徵值很小的，基本上就可以被忽略了。
主成分分析範例 1 (Rank=2)
為了展示上述的數學論點，我們用 R 軟體建構出 4 組樣本，每組有 25 個元素，其中第 3, 4 組是第 1, 2 組的線性組合，因此這個 4*25 矩陣的 rank 將只有 2，所以透過主成分分析，我們應該會看到只有兩個主成分。
以下是我們的範例程式。
> x1=rnorm(25, mean=5, sd=1) # x1 是常態分布隨機產生的 25 個樣本
> x2=rnorm(25, mean=5, sd=1) # x2 是常態分布隨機產生的 25 個樣本
> x3=x1+x2 # x3=x1+x2, 是 x1, x2 的線性組合
> x4=x1+2*x3 # x4=x1+2*x3=x1+2*(x1+x2)=3x1+2x2, 因此也是 x1, x2 的線性組合。
> x14 = data.frame(x1, x2, x3, x4) # 用這四組樣本建立一個 frame 變數 x14
> pr = princomp(x14, cor=TRUE) # 開始進行主成分分析
> summary(pr, loading=TRUE) # 顯示主成分分析的結果
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4
Standard deviation 1.7281767 1.0066803 4.712161e-08 8.339758e-09
Proportion of Variance 0.7466487 0.2533513 5.551115e-16 1.738789e-17
Cumulative Proportion 0.7466487 1.0000000 1.000000e+00 1.000000e+00
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4
x1 -0.449 0.626 0.637
x2 -0.367 -0.768 0.495 0.176
x3 -0.576 -0.311 -0.750
x4 -0.576 -0.502 0.638
> 在上述分析結果中，我們看到累積貢獻比率 (Cumulative Proportion) 在第一主成分 Comp.1 上為 0.7466487， 而累積到第二主成分 Comp.2 時就達到 1.0 了，這代表只要用兩個主成分就可以建構出整個樣本集合。
根據 Loadings 中的 Comp.1 那一列可知，第一主成分 Comp.1 = -0.449 x1 - 0.367 x2 - 0.576 x3 - 0.576 x4， 也就是我們用這個主成分就可以掌握整組資料的 7 成 (0.7466487)，而加上第二主成份 Comp.2 = 0.626 x1 - 0.768 x2 之後， 就可以掌握 100% 的資料，完全重建整個矩陣了。(因為這組資料的 rank 為 2)。
主成分分析範例 2 (Rank=3)
為了驗證上述的「線性代數」想法，我們接著將 x3 改掉，成為獨立常態序列，然後讓 x4=3x1+2x2+x3，如下列程式所示。
> x1=rnorm(25, mean=5, sd=1) # x1 是常態分布隨機產生的 25 個樣本
> x2=rnorm(25, mean=5, sd=1) # x2 是常態分布隨機產生的 25 個樣本
> x3=rnorm(25, mean=5, sd=1) # x3 是常態分布隨機產生的 25 個樣本
> x4=3*x1+2*x2+x3 # x4=3*x1+2*x2+x3, 是 x1, x2, x3 的線性組合
> x14 = data.frame(x1, x2, x3, x4) # 用這四組樣本建立一個 frame 變數 x14
> pr = princomp(x14, cor=TRUE) # 開始進行主成分分析
> summary(pr, loading=TRUE)) # 顯示主成分分析的結果
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4
Standard deviation 1.4659862 1.1233489 0.767445 4.712161e-08
Proportion of Variance 0.5372789 0.3154782 0.147243 5.551115e-16
Cumulative Proportion 0.5372789 0.8527570 1.000000 1.000000e+00
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4
x1 0.634 0.104 0.458 0.615
x2 0.310 -0.669 -0.625 0.259
x3 0.194 0.736 -0.632 0.146
x4 0.682 -0.731您可以看到在下列的累積貢獻比率 (Cumulative Proportion) 當中，要到第三個主成分才到達 1.0，而非第二個主成分。
Cumulative Proportion 0.5372789 0.8527570 1.000000 1.000000e+00而且在標準差 (Standard deviation) 與 變異比率 (Proportion of Variance) 上也反映了類似的情況，必須要到 Comp.4 的時候， 這兩個數值才會突然下降到幾近為 0 的程度 (4.712161e-08, 5.551115e-16)。
主成分分析範例 3 (Rank=3 加上隨機誤差)
接著、讓我們為 x4 加上一點隨機誤差，看看主成分分析的結果會有何改變。
> x1=rnorm(25, mean=5, sd=1) # x1 是常態分布隨機產生的 25 個樣本
> x2=rnorm(25, mean=5, sd=1) # x2 是常態分布隨機產生的 25 個樣本
> x3=rnorm(25, mean=5, sd=1) # x3 是常態分布隨機產生的 25 個樣本
> x4=3*x1+2*x2+x3+rnorm(25, mean=0, sd=1) # x4=3*x1+2*x2+x3, 是 x1, x2, x3 的線性組合加上常態隨機誤差
> x14 = data.frame(x1, x2, x3, x4) # 用這四組樣本建立一個 frame 變數 x14
> pr = princomp(x14, cor=TRUE) # 開始進行主成分分析
> summary(pr, loading=TRUE)) # 顯示主成分分析的結果
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4
Standard deviation 1.4565751 1.1233728 0.7704314 0.151189097
Proportion of Variance 0.5304027 0.3154916 0.1483911 0.005714536
Cumulative Proportion 0.5304027 0.8458943 0.9942855 1.000000000
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4
x1 -0.642 0.117 0.410 0.637
x2 -0.306 -0.662 -0.645 0.228
x3 -0.173 0.740 -0.641 0.103
x4 -0.681 -0.729
> 您可以看到在累積貢獻比率 (Cumulative Proportion) 當中，到了第三主成分時已經達到 99.4% (0.9942855)， 而到了第四主成分時才達到 100%，這代表若用前三個主成份重建仍然會有少許誤差。
Cumulative Proportion 0.5304027 0.8458943 0.9942855 1.000000000上述的誤差量可以從標準差 (Standard deviation) 與 變異比率 (Proportion of Variance) 這兩組數字上看到。
Comp.1 Comp.2 Comp.3 Comp.4
Standard deviation 1.4565751 1.1233728 0.7704314 0.151189097
Proportion of Variance 0.5304027 0.3154916 0.1483911 0.005714536因子分析
另外、還有一個與主成分分析用法相當類似的方法，稱為因子分析 (Factor Analysis)，這種方法的使用與主成分分析 之差異點，在於必須指定要事先指定使用多少因子，如果使用的因子過多，則會導致失敗的結果。
以下是我們同樣針對上述範例所進行的因子分析結果，您可以發現在下列的分析中，只有指定一個因子的時候可以成功 的進行分析，而指定兩個以上的因子時，就會導致分析失敗的結果。
> x1=rnorm(25, mean=5, sd=1) # x1 是常態分布隨機產生的 25 個樣本
> x2=rnorm(25, mean=5, sd=1) # x2 是常態分布隨機產生的 25 個樣本
> x3=rnorm(25, mean=5, sd=1) # x3 是常態分布隨機產生的 25 個樣本
> x4=3*x1+2*x2+x3+rnorm(25, mean=0, sd=1) # x4=3*x1+2*x2+x3, 是 x1, x2, x3 的線性組合加上常態隨機誤差
> x14 = data.frame(x1, x2, x3, x4) # 用這四組樣本建立一個 frame 變數 x14
> fa = factanal(x14, factors=2)
錯誤在factanal(x14, factors = 2) :
2 factors is too many for 4 variables
> fa = factanal(x14, factors=1)
> fa
Call:
factanal(x = x14, factors = 1)
Uniquenesses:
x1 x2 x3 x4
0.126 0.834 0.951 0.005
Loadings:
Factor1
x1 0.935
x2 0.407
x3 0.222
x4 0.998
Factor1
SS loadings 2.084
Proportion Var 0.521
Test of the hypothesis that 1 factor is sufficient.
The chi square statistic is 21.97 on 2 degrees of freedom.
The p-value is 1.7e-05
> fa = factanal(x14, factors=3)
錯誤在factanal(x14, factors = 3) :
3 factors is too many for 4 variables結語
從主成分分析這個案例中，我們可以看到「機率統計」技術背後的原理，竟然是「線性代數」，數學果然是一門博大精深的學問啊！
事實上、上一期的「迴歸分析」主題，背後的原理乃是「最小平方法」，必須用到「微積分」與「線性代數」進行理論解釋。
我想、這也是為甚麼大學資工系的課程當中，「微積分、線性代數、離散數學、機率統計」通常是必修的原因啊！
參考文獻
- R语言与统计分析, 作者: 汤银才, ISBN: 9787040250626。