前言
編輯小語
在本期的「程式人雜誌」的人物速寫中,聚焦的主題是「高通公司」的兩位創辦人 (Viterbi 與 Jacobs) ,以及這兩位創辦人所開創的 Linkabit 與高通公司,描述一個由他們寫下的數位通訊產業傳奇故事。
在程式與科學主題中,我們延續上期未介紹完的「電磁學」主題,介紹電磁學與向量微積分的關係,並說明馬克斯威方程式的意義。
另外還有關於 Qt, GTKWave, Raspberry Pi 等主題的介紹與討論,並且在影音頻道中介紹了 LTSpice 這個軟體的入門影片。
當然、在程式人文集當中,我們同樣有關於「Arduino、JavaScript、R、Verilog 與開放電腦計畫」的文章,讓大家可以吸收到 專業的程式資訊,希望您會喜歡這些文章。
---- (程式人雜誌編輯 - 陳鍾誠)
授權聲明
本雜誌採用 創作共用:姓名標示、相同方式分享 授權,若您想要修改本書產生衍生著作時,至少應該遵守下列授權條件:
- 標示原作者姓名
- 採用 創作共用:姓名標示、相同方式分享 的方式公開衍生著作。
另外、當本雜誌中有文章或素材並非採用 姓名標示、相同方式分享 時,將會在該文章或素材後面標示其授權,此時該文章將以該標示的方式授權釋出,請修改者注意這些授權標示,以避免產生侵權糾紛。
例如有些文章可能不希望被作為「商業性使用」,此時就可能會採用創作共用:姓名標示、非商業性、相同方式分享 的授權,此時您就不應當將該文章用於商業用途上。
最後、懇請勿移除公益捐贈的相關描述,以便讓愛心得以持續散播!
程式人短訊
程式短訊:開源視窗程式函式庫 - Qt 與 Qt Creator
Qt 是一套用 C++ 開發的視窗函式庫,Qt Creator 則是在 Qt 上的一套視覺化介面開發工具,以下是一段用 Qt Creator 開發簡易視窗程式的影片。
Qt 是由 Haavard Nord 和 Eirik Chambe-Eng 於1991年開始開發的,並在 1994年3月4日成立 Quasar Technologies 這家公司, 後來公司更名為 Trolltech (中文「奇趣科技」)。
2008 年 6 月 17 日 Trolltech 被 Nokia 收購,並更名為 Qt Software。然後 Nokia 在 2009 年 5 月 11 日宣布將 Qt 開放原始碼。
後來 Nokia 又在 2011 年將 Qt商業授權業務轉給 Digia,並在 2012 年 8 月 9 日將 Qt 完全賣給 Digia ,現在的 Qt 是由 Digia 主導商業授權的。
Qt 採用多重授權機制,如果您願意開放原始碼,可用 「LGPLv2.1 的 授權方式」 (有例外條款, 也可以改採 GPLv3 的授權方式 ), 如果不願意開放原始碼,則可以付費給 Digia 公司採用「商業授權 」。
筆者看過一些開放原始碼人士的評論,通常認為 Qt 比 GTK+ 好用,因此若您需要設計開放原始碼的視窗程式,可以考慮使用 Qt + Qt Creator 來發展,應該會比較順利。
參考文獻
- http://zh.wikipedia.org/wiki/Qt_Creator
- http://zh.wikipedia.org/wiki/Qt
- http://zh.wikipedia.org/wiki/Digia
- http://en.wikipedia.org/wiki/Qt_(software)
【本文由陳鍾誠取材並修改自 維基百科 ,採用創作共用的 姓名標示、相同方式分享 授權】
軟體短訊:開源波型顯示軟體 - GTKWave
GTKWave 是採用 GTK+ 函式庫設計出來的一個開放原始碼的波形顯示工具,可以讀取 FST, LXT, LXT2, VZT, GHW, VCD/EVCD 等 檔案格式,並且進行波形的互動式顯示,其原始開發平台是 Linux,但也有被移植到 Windows, Mac OS X 等作業系統上。
GTKWave 被 GNU 收錄在開放原始碼的 gEDA 工具平台中,也被開放原始碼的 Verilog 模擬工具 Icarus 納入後用來顯示輸出 的 VCD 格式波形檔。
GTKWave 除了顯示波形以外,也可以將整組 n 條線顯示為「整數、實數、ASCII 字元、二進位、八進位、十進位、十六進位」等等, 因此很適合用來做為 Verilog/VHDL 等模擬軟體的顯示工具。
以下是 GTKWave 的官方下載網址
如果您想安裝 Windows 版本的話,可以從以下網址下載:
如果您有安裝 icarus for windows 的話,那麼裡面預設就有安裝 GTKWave,以下是 icarus for windows 的網址:
通常 icarus for windows 會將 GTKwave 放在 C:\iverilog\bin\gtkwave.exe 這個路徑下,您可以自行點選使用。
以下文件說明了如何讓 icarus 輸出波形的 VCD 格式檔,以及如何用 GTKWave 顯示這些波形的方法。
其中的關鍵是要使用 $dumpfile("dff.vcd"); 與 $dumpvars; 等兩個指令,去輸出波形到 dff.vcd 檔案中。
$dumpfile("dff.vcd");
$dumpvars;當您用 iverilog -o dff dff.v 指令編譯完程式並用 vvp dff 進行模擬後,就會輸出 dff.vcd 這個檔案, 然後您可以開啟 GTKwave,接著將 dff.vcd 拖到 GTKwave 視窗中,再選取所要顯示的變數,放入 signal 窗框裡, 接著可以點選放大鏡圖示中的 Zoom Fit 功能,這樣就可以將波形完全顯示在視窗中。
如果您想調整顯示大小,可以用放大鏡圖示中的 +, - 功能,進行微調的動作,以便能用互動的方式觀察波形, 看看程式的模擬結果是否正確。
接著、讓我們實際用 icarus 輸出波形的 VCD 檔,並用 GTKwave 來看看這些波形。
以下是筆者所寫的一個 veriog 程式 alu.v ,該程式是一個 ALU 模組:
檔案:alu.v
// 輸入 a, b 後會執行 op 所指定的運算,然後將結果放在暫存器 y 當中
module alu(input [7:0] a, input [7:0] b, input [2:0] op, output reg [7:0] y);
always@(a or b or op) begin // 當 a, b 或 op 有改變時,就進入此區塊執行。
case(op) // 根據 op 決定要執行何種運算
3'b000: y = a + b; // op=000, 執行加法
3'b001: y = a - b; // op=000, 執行減法
3'b010: y = a * b; // op=000, 執行乘法
3'b011: y = a / b; // op=000, 執行除法
3'b100: y = a & b; // op=000, 執行 AND
3'b101: y = a | b; // op=000, 執行 OR
3'b110: y = ~a; // op=000, 執行 NOT
3'b111: y = a ^ b; // op=000, 執行 XOR
endcase
$display("base 10 : %dns : op=%d a=%d b=%d y=%d", $stime, op, a, b, y); // 印出 op, a, b, y 的 10 進位值。
$display("base 2 : %dns : op=%b a=%b b=%b y=%b", $stime, op, a, b, y); // 印出 op, a, b, y 的 2 進位值。
end
endmodule
module main; // 測試程式開始
reg [7:0] a, b; // 宣告 a, b 為 8 位元暫存器
wire [7:0] y; // 宣告 y 為 8 位元線路
reg [2:0] op; // 宣告 op 為 3 位元暫存器
alu alu1(a, b, op, y); // 建立一個 alu 單元,名稱為 alu1
initial begin // 測試程式的初始化動作
a = 8'h07; // 設定 a 為數值 7
b = 8'h03; // 設定 b 為數值 3
op = 3'b000; // 設定 op 的初始值為 000
$dumpfile("alu.vcd");
$dumpvars;
end
always #50 begin // 每個 50 奈秒就作下列動作
op = op + 1; // 讓 op 的值加 1
end
initial #1000 $finish; // 時間到 1000 奈秒就結束
endmodule然後我們可以用下列指令編譯 alu.v 程式並執行之:
D:\verilog>iverilog -o alu alu.v
D:\verilog>vvp alu
VCD info: dumpfile alu.vcd opened for output.
base 10 : 0ns : op=0 a= 7 b= 3 y= 10
base 2 : 0ns : op=000 a=00000111 b=00000011 y=00001010
base 10 : 50ns : op=1 a= 7 b= 3 y= 4
base 2 : 50ns : op=001 a=00000111 b=00000011 y=00000100
base 10 : 100ns : op=2 a= 7 b= 3 y= 21
base 2 : 100ns : op=010 a=00000111 b=00000011 y=00010101
base 10 : 150ns : op=3 a= 7 b= 3 y= 2
base 2 : 150ns : op=011 a=00000111 b=00000011 y=00000010
base 10 : 200ns : op=4 a= 7 b= 3 y= 3
base 2 : 200ns : op=100 a=00000111 b=00000011 y=00000011
base 10 : 250ns : op=5 a= 7 b= 3 y= 7
base 2 : 250ns : op=101 a=00000111 b=00000011 y=00000111
base 10 : 300ns : op=6 a= 7 b= 3 y=248
base 2 : 300ns : op=110 a=00000111 b=00000011 y=11111000
base 10 : 350ns : op=7 a= 7 b= 3 y= 4
...接著可開啟 GTKWave 軟體,然後將輸出的 alu.vcd 檔拖到 GTKWave 視窗中,然後點選 main/alu1 的模組,會發現 裡面有 a, b, op, y 等訊號變數,將這些變數一一拖到 signals 窗框中,就可以看到如下的訊號畫面。
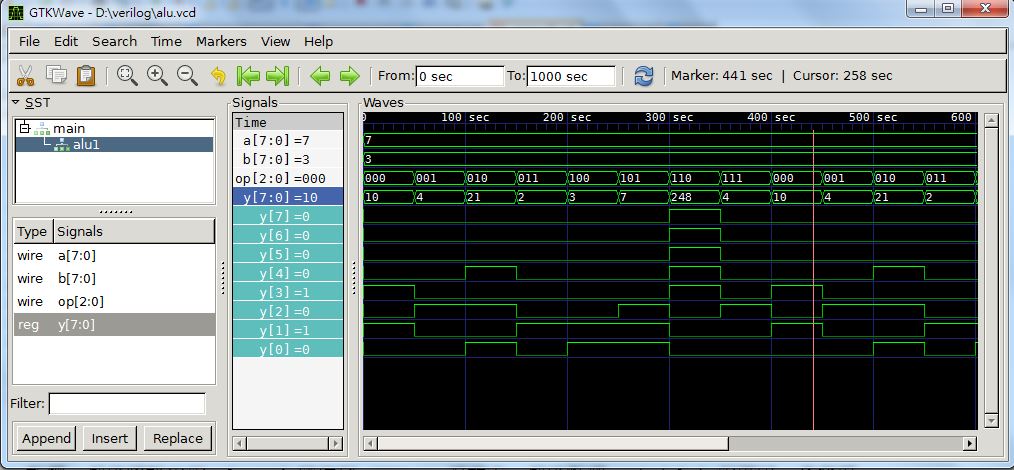
圖、用 GTKwave 檢視波形檔 alu.vcd 的畫面
說明:上述畫面筆者在 signals 的 a,b, y 等訊號上,按右鍵選擇了 DataFormat/Decimal ,就可以將這些變數以十進位 的方式顯示。(如果想用 16 進位的方式,可按右鍵選擇 DataFormat/Hex)。
參考文獻
【本文由陳鍾誠取材並修改自 維基百科,採用創作共用的 姓名標示、相同方式分享 授權】
人物速寫
高通共同創辦人: Andrew Viterbi
安德魯·詹姆斯·維特比(英語:Andrew James Viterbi,1935年3月9日-)是一位義大利-美國電機工程師和企業家,高通公司的共同創建者之一。

圖、Andrew Viterbi 1963 年初任教師時的照片
來源:The Quiet Genius:Andrew J. Viterbi 一文中的插圖
(本圖版權屬於 Trudy E. Bell, 在此僅依著作權合理使用的法條取用,使用時請注意)
Viterbi 生於義大利貝爾加莫的一個猶太家庭,1939年隨父母移居美國。1952年進入麻省理工學院就讀,1957年獲該校電力工程理學士學位。 後進入噴氣推進實驗室,為開發鎖相環做了一定的工作。1963年取得了南加州大學數位通訊領域 (digital communications) 的 博士學位。他後來申請到了加州大學洛杉磯分校 University of California, Los Angeles (UCLA) 的教職。
1967年他發明了 Viterbi 演算法,該演算法可用來解碼卷積編碼數據 (Convolutional Code),是一種糾錯碼的演算法。這個演算法在「數位通訊」、「人工智慧的隱碼可夫鏈模型」、以及「自然語言處理和語音辨識系統」上都有重要的用途。
除了 Viterbi 演算法之外,他在 Code Division Multiple Access (CDMA) 無線通訊上,也有很多重要的貢獻,這也是為何他後來與 Irwin M. Jacobs 兩人,在 1985 年聯手所創造出的高通 (Qualcomm) 公司,會成為 3G 無線網路領域的龍頭之原因。
事實上、他在 1968 年就與 Irwin M. Jacobs 及 Leonard Kleinrock 兩人聯手創立過一家 Linkabit 公司,後來 Leonard Kleinrock 離開了。
雖然 Linkabit 本身並沒有成長到非常大,但是在美國科技史上卻有無比重要的地位,因為從 Linkabit 衍生出了七十二家公司 (包含高通公司),這些公司在美國形成了一整個產業群。因此 Linkabit 可以說是美國無線數位通訊產業的育成中心,就像辦導體的發明人之一 William Shockley 所創立的快捷半導體 (Fairchild Semiconductor) 是美國 IC 半導體領域的育成中心地位一樣。
在美國科技產業史上,Linkabit、Fairchild 與全錄 Xerox PARC 研究中心,都是本身並沒有賺到很多錢,但是卻成功的創造出驚人的技術,然後衍生出一整個產業的公司。如果您想研究科技產業史,這些公司的發展歷史將會是非常值得研究的對象。
參考文獻
- Wikipedia:Andrew Viterbi
- Wikipedia:Viterbi Algorithm
- 維基百科:安德魯·維特比
- 維基百科:維特比演算法
- The Quiet Genius:Andrew J. Viterbi, by Trudy E. Bell
- Wikipedia:Viterbi Decoder
- The Viterbi Algorithm: A Personal History, G. David Forney, Jr.
- Error bounds for convolutional codes and an asymptotically optimum decoding algorithm, Viterbi , Andrew J.
- Wikipedia:Convolutional Code
- Introduction to Convolutional Codes, Part II, Frans M.J. Willems, Eindhoven University of Technology
- 維基百科:快捷半導體公司
【本文由陳鍾誠取材並修改自 維基百科,內文採用創作共用的 姓名標示、相同方式分享 授權,圖片版權屬於原作者 Trudy E. Bell,使用時請注意】
高通共同創辦人兼 CEO:Irwin M. Jacobs
厄文·馬克·雅各布(英語:Irwin Mark Jacobs,1933年10月18日-),生於美國麻塞諸塞州新伯福,是一位美國的電機工程師,並且是高通公司的共同創辦者以及前執行長。

圖、Irwin Jacobs
來源:http://en.wikipedia.org/wiki/File:Irwin_Jacobs.jpg
Jacobs 於 1956 年從康乃爾大學電機工程學系畢業,1957年取得麻省理工學院電機與電腦科學碩士,1959年取得博士。畢業後,在1959年至1966年間,在麻省理工學院電機系擔任助教、助理教授。 1966 年至 1972 年間,於聖地牙哥加利福尼亞大學擔任教授。並在 1965年,出版《通訊工程原理》(Principles of Communication Engineering),成為一本很經典的教科書。
雖然 Jacobs 並不像另一位共同創辦人 Andrew Viterbi 一樣有留下與自己名字相同的 Viterbi 演算法,但是他在高通卻是真正的靈魂人物,這個故事要從高通的前身, Linkabit 這家公司說起。
話說 1968 年就與 Jacobs , Viterbi 與 Kleinrock 創辦了 Linkabit 後不久, Kleinrock 就離開了,不過這三個人創辦人全都是怪傑,Kleinrock 後來成為 ARPANET 的主要創造者,也就是今日 Internet 的前身。
Linkabit 成立後接了不少軍方的衛星通訊訂單,生意蒸蒸日上,平均每年成長超過 50%,在 10 年內從原本只有 3 名員工成長到超過 600 名員工。
然後、在某個機緣下,Linkabit 被 M/A-COM (前身為微波通訊--Microwave Associates) 這家公司給併購了,因為 Jacobs 與 M/A-COM 的執行長「拉里、古爾德」認為兩家公司業務互補,合併之後應該會更好,因此雙方同意在 1980 年合併為 M/A-COM linkabit。
但是不久後「拉里、古爾德」與公司的其他高層不合,結果離開了 M/A-COM linkabit,於是執行長就換人做了。
但是新任執行長比較功利主義,只想賺錢卻不想進行長遠研發投資,結果 Jacobs 等人開始落入困境,總是要花很多時間去搞政治鬥爭並爭取研發經費。
於是在 1985 年 4 月 1 日愚人節的晚上, Jacobs 提著空箱子進入辦公室,打包走人了。
幾個月後, Jacobs 決定要創立新公司,於是邀請原先在 Linkabit 的 5 位合作夥伴到家裡聚會,幾天後他與這五位夥伴,加上原本 linkabit 的共同創辦人 Viterbi 總共 7 位,一同成立了高通 (Qualcomm) 公司。
M/A-COM 新執行長的短視作風,讓很多原本 Linkabit 的傑出工程師都很受不了,結果這些人也紛紛的都出去創業了,其中很多人的創業都相當成功,這些人的貢獻讓美國的數位通訊產業蓬勃發展。
1993 年,也就是在 Linkabit 成立 25 週年的餐會上,這些 Linkabit 的前員工辦了一次聚會,並且在聚會時畫下了一張 Linkabit 的家族樹,後來這張家族樹繼續延伸,總共算出至少有 75 家公司從 Linkabit 衍生出來,這讓 Linkabit 成為美國歷史上最成功的「育成中心」之一。
這一切的一切,都得感謝 M/A-COM 那位短視的繼任執行長!
看過了高通電信 (Qualcomm) 與快捷半導體 (Fairchild) 的例子之後,我得到一個啟示:
當一個好老板領導著一群偉大工程師的時候,那只會是一家偉大的公司而已。
當一個爛老板管理著這群偉大工程師的時候,卻可能創造出一個偉大的產業!
這讓我想起了聖經裏的這句話:
我實實在在地告訴你們,一粒麥子不落在地裡死了,仍舊是一粒,若是死了,就結出許多子粒來。
Truly I say to you, If a seed of grain does not go into the earth and come to an end, it is still a seed and no more; but through its death it gives much fruit.
-《聖經》約翰福音12章24節
參考文獻
- Wikipedia:Irwin M. Jacobs
- Wikipedia:Qualcomm
- Wikipedia:Leonard Kleinrock
- Wikipedia:ARPANET
- 書籍:高通方程式, 作者: Dave Mock, 人民郵電出版社翻譯, 出版日期:2005-10-01.
【本文由陳鍾誠取材並修改自 維基百科,採用創作共用的 姓名標示、相同方式分享 授權】
影音頻道
看影片學 LTSpice 類比電路設計工具
SPICE 是一種為 IC 積體電路開發的類比電路模擬程式(英語:Simulation Program with Integrated Circuit Emphasis, SPICE),是 1975 年由加州大學伯克萊分校的 Donald Pederson 在電子研究實驗室創建的。
第一版和第二版都是用 Fortran 語言編寫的,但是從第三版開始用 C 語言編寫。從一個稱為 CANCER 的電路模擬程式開始,發展出今日幾乎被全世界公認為電路模擬標準的 SPICE 原始雛型程式。
OrCAD 的 PSpice 是 2000 年之前在個人電腦上最常被大專院校使用的 SPICE 軟體版本。以下是 PSPICE 9.1 student version 這個軟體的下載連結。
但是 OrCAD 在 2000 年被 Cadence Design System 收購之後,似乎就沒有對免費版的 PSpice 進行更新的動作。因此,若想要使用免費的 Spice 軟體,除了使用老舊的 PSPICE 9.1 學生版之外,可能就要改用其他軟體。
雖然開放原始碼有一套 ngspice,但似乎功能並不好用,不是很多人推薦。開放原始碼領域似乎也沒有任何一套 SPICE 軟體被強烈推薦的。
在免費的商用軟體中,TINA 與 LTSpice 是常被提到的兩套 SPICE 軟體,但是似乎 LTSpice 的風評較好,以下是一些相關的討論與文章。
- Looking to write electrical engineering related open software
- All About Circuits Forum > Electronics Forums > General Electronics Chat Reload this Page LTSpice vs. Tina-TI
由於筆者近來想要找一套 SPICE 的軟體來學習類比電路模擬,於是決定採用在 LTSpice 軟體作為學習工具,因此我上網找了一些的教學影片,以便學習這個軟體。
以下是筆者建議的第一個入門影片:
上述影片建立了一個最簡單的電阻電路,如下圖所示:
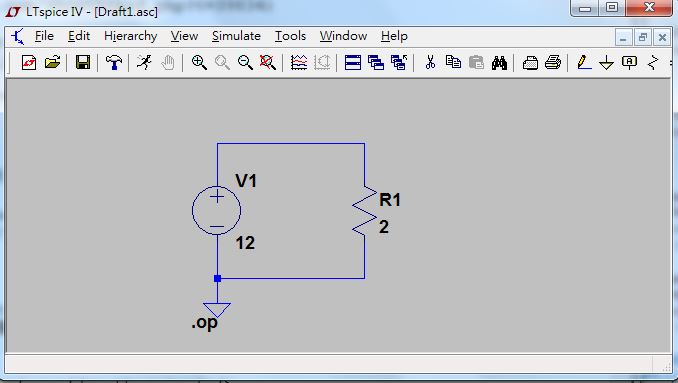
圖、電阻電路 V=IR, 12V =2 A * 6 Ω
以上這個電路與示範影片真的很簡單,只要知道 V=IR 這個公式的人應該都可以輕易理解。
接著您可以看看 YouTube 的上傳者 Terry Sturtevant 所給的 10 部 LTSpice 教學影片, 這些影片都很短,每片都只有幾分鐘:
這樣,您應該就可以瞭解如可使用 LTSpice 來學習類比電路設計了,接下來就是 將電路學上所學到的電路放到 LTSpice 裏面進行測試,這樣應該就能更深入的體會 各種模型的意義了。
參考文獻
- 維基百科:OrCAD PSpice
- 維基百科:SPICE
- Wikipedia:SPICE
- Wikipedia:LTSpice
- Interactive LTSpice Tutorial
【本文由陳鍾誠取材並修改自 維基百科,採用創作共用的 姓名標示、相同方式分享 授權】
程式人討論區
討論:如何用 Raspberry Pi 插一根電線就能發送 FM 訊號
網友 Albert Huang 分享了一個很有趣的網頁,說到可以用一個稱為 PiFm 的程式,讓 Raspberry Pi 將 wav 的聲音檔 透過在 GPIO 4 上插一根導線,就可以發送出該聲音的 FM 電磁波訊號。
Albert Huang 的說明如下:
用 Raspberry GPIO 4 的 Alt1 功能(GPCLK0)來傳送 FM 訊號,利用了因為頻寬限制, GPCLK0 超過 75MHz 之後,就會由方波而愈來愈接近正弦波的原理,而 FM 就是依據輸入的聲音大小來改變 FM 的載波頻率。
以下是在程式人雜誌社團中的原始討論:
為了更清楚瞭解到底這是如何運作的,我找到了以下兩個影片,應該可以很清楚的看到運作的過程。
- YouTube:Turning the Raspberry Pi into an FM transmitter with PiFM
- YouTube:Raspberry Pi as FM Transmitter
看完這兩個影片之後,我真的很想知道他是怎麼做的,所以我找到該模組的用法與原始程式下載點:
使用方法如下:
sudo python
>>> import PiFm
>>> PiFm.play_sound("sound.wav")PiFm 模組的程式總共包含兩個部份,分別是 Python (PyFm.py) 與 C (PyFm.c) 的程式,但我想主要的重點是 C 的程式,以下是我認為關鍵的部份。
void playWav(char* filename, float samplerate)
{
int fp= STDIN_FILENO;
if(filename[0]!='-') fp = open(filename, 'r');
//int sz = lseek(fp, 0L, SEEK_END);
//lseek(fp, 0L, SEEK_SET);
//short* data = (short*)malloc(sz);
//read(fp, data, sz);
int bufPtr=0;
float datanew, dataold = 0;
short data;
for (int i=0; i<22; i++) // 掠過 wav 檔的表頭
read(fp, &data, 2); // read past header
while (read(fp, &data, 2)) {
// fmconstant = 22500 * 50e-6 = 1.125
float fmconstant = samplerate * 50.0e-6; // for pre-emphisis filter. 50us time constant
// wav 取樣頻率一般有11025Hz(11kHz) ,22050Hz(22kHz) 和44100Hz(44kHz)三種,此檔案用 22050Hz
int clocksPerSample = 22500.0/samplerate*1400.0; // for timing
// 主程式中有 playWav(argv[1], argc>3?atof(argv[3]):22500);
// 所以 22500.0/samplerate = 1, 於是 clocksPerSample =1400,也就是最小震盪週期會被取 1400 次樣本。
datanew = (float)(data)/32767; // 將資料 data 轉為浮點數
float sample = datanew + (dataold-datanew) / (1-fmconstant); // fir of 1 + s tau
float dval = sample*15.0; // actual transmitted sample. 15 is bandwidth (about 75 kHz)
int intval = (int)(round(dval)); // integer component
float frac = (dval - (float)intval)/2 + 0.5;
unsigned int fracval = frac*clocksPerSample;
bufPtr++;
// 用直接記憶體映射 DMA 的方法,將資料往 GPIO4 的 allof7e 輸出
// 參考: 树莓派处理器BCM2835的DMA -- http://www.lijingquan.net/dma-bcm2835-rpi.html
while( ACCESS(DMABASE + 0x04 /* CurBlock*/) == (int)(instrs[bufPtr].p)) usleep(1000);
((struct CB*)(instrs[bufPtr].v))->SOURCE_AD = (int)constPage.p + 2048 + intval*4 - 4 ;
bufPtr++;
while( ACCESS(DMABASE + 0x04 /* CurBlock*/) == (int)(instrs[bufPtr].p)) usleep(1000);
((struct CB*)(instrs[bufPtr].v))->TXFR_LEN = clocksPerSample-fracval;
bufPtr++;
while( ACCESS(DMABASE + 0x04 /* CurBlock*/) == (int)(instrs[bufPtr].p)) usleep(1000);
((struct CB*)(instrs[bufPtr].v))->SOURCE_AD = (int)constPage.p + 2048 + intval*4+4;
bufPtr=(bufPtr+1) % (1024);
while( ACCESS(DMABASE + 0x04 /* CurBlock*/) == (int)(instrs[bufPtr].p)) usleep(1000);
((struct CB*)(instrs[bufPtr].v))->TXFR_LEN = fracval;
dataold = datanew;
}
close(fp);
}然後我找到維基百科的調頻原理,理面有解說如何將訊號用調頻的方式調變的概念,連結如下:
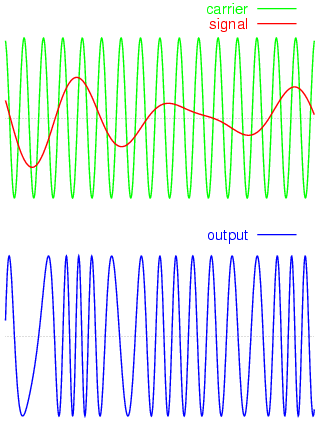
圖、FM 調頻的原理
但是,要如何用 Raspberry Pi 去送出經過調頻的方式調變的訊號呢?經過我研究與查詢後,我發現 PiFm 好像是利用 GPIO4 裏面的「脈衝寬度調變」(Pulse Width Modulation, PWM) 功能 (Alt1 , GPCLK0),來輸出 FM 調變過後的訊號。
例如下列的 raspberry-gpio-python 專案就有之援類似的功能。
- raspberry-gpio-python -- https://code.google.com/p/raspberry-gpio-python/wiki/PWM
因此、我們必須瞭解一下何謂 PWM,以下維基百科的解釋與圖片說明了這項功能的原理。
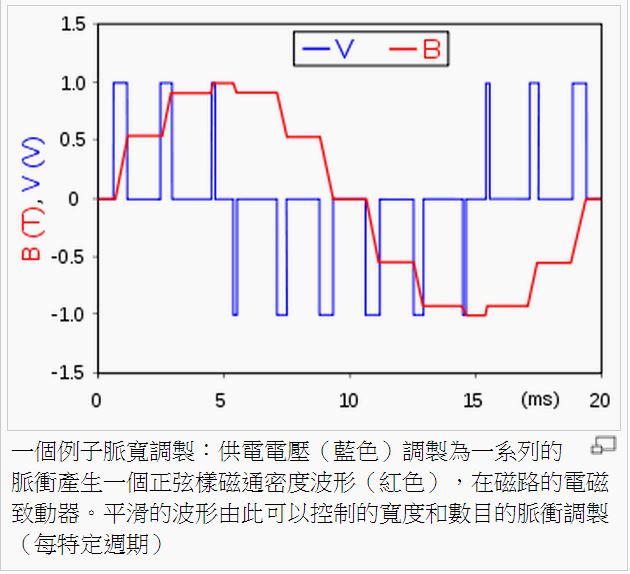
圖、PWM 脈衝寬度調變的原理
與類比電路不同,數字電路是在預先確定的範圍內取值,在任何時刻,其輸出只可能為ON和OFF兩種狀態,所以電壓或電流會通/斷方式的重複脈衝序列載入到類比負載。PWM技術是一種對類比信號電平的數字編碼方法,通過使用高解析度計數器(調製頻率)調製方波的占空比,從而實現對一個類比信號的電平進行編碼。
類比信號能否使用PWM進行編碼調製,僅依賴頻寬,這即意味著只要有足夠的頻寬,任何類比信號值均可以採用PWM技術進行調製編碼,一般而言,負載需要的調製頻率要高於10Hz,在實際應用中,頻率約在1kHz到200kHz之間。
程式可以透過對 PWM port 輸出 (Frequency, Duty cycle) 兩個參數的方式,控制訊號的 PWM 調變,以下文章與影片有較詳細的說明。
- Raspberry pi has PWM pins, Posted by praveen kumar at 07:05
- YouTube:Using PWM with RPi.GPIO and Python on the Raspberry Pi
我猜測 PiFm 就是利用這個功能,對 GPCLK0 輸出不同的方波 (上圖中藍色 V 的部份),這些方波會控制 PWM 讓它輸出紅色的波形,這些紅色的波形會近似 wav 檔內所代表的波形,於是就能將 wav 檔的聲音以 FM 的方式傳送出去了。
透過上述方式,我們可以用 Raspberry Pi 裏 「CPU+程式」的方式,輸出訊息給 PWM port ,以便將 wav 檔中的訊號,用 FM 的方式調變後輸出,於是「程式人」也可以學如何用 Raspberry Pi 發送「電磁波」,不需要靠額外的板子或 IC 了。
這種做法真棒!
參考文獻
- 树莓派处理器BCM2835的DMA
- 維基百科:頻率調變 , (FM)
- 維基百科:脈衝寬度調變
- RPIO.PWM, PWM via DMA for the Raspberry Pi
- Raspberry pi has PWM pins
- PiHAT - Rasberry Pi Home Automation Transmitter
- Using a Raspberry Pi as an AirPlay Receiver
程式與科學
電磁學基礎 (2) -- 向量微積分 (作者:陳鍾誠)
在上一期當中,我們已經介紹了電磁學的一些基本概念,該文網址如下:
在本期當中,我們將會說明電磁學的理論基礎,特別是有關向量微積分的部份。
前言
為了要描述「力場、電場、磁場」等這些概念,物理學家與數學家發展出了通用的「向量場」觀念, 這些觀念與微積分中的「無窮小」概念整合後,就發展出了「通量、環量、散度、旋度」等等數學 描述,透過這些數學描述,我們就能更快速的進入「馬克斯威」的電磁理論領域。
通量與散度
在一個向量場當中,通量是指通過某個表面的向量總數,通常用積分的方式累加計算,例如在以下的圖 (a) 中,由於該粒子帶正電,會對其它正電粒子產生排斥力,因此其電場是向外發射的,於是若我們在電子外部加一個包覆球面, 那麼通過該球面的電通量就會是正的,而且電通量大小就會是該粒子的電量大小。
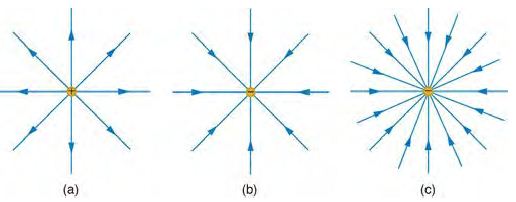
圖、電場與電通量
同樣的、在圖 (b) 中由於粒子帶負電,會對其它正電粒子產生吸引力,因此其電場是向內集中的,所以通過包覆球面的電通量就會是負的。
如果該帶電粒子的電量較大,那麼我們通常會把電場線畫多一點,這種較密集的電場線在視覺上可以強調哪一部份的電場較強, 如以上的圖 (c) 所示。
看過這個範例,我們就可以來正式定義「通量」的概念了。
定義:通量
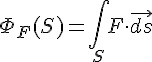
直覺意義:
F 是一個向量場 (例如電場),S 是一個曲面。
代表向量場與曲面法向量的內積。
向量場 F 與整個曲面 S 的法向量內積總和,即是通量。
通量大於零 (通量 > 0) 代表有向外發射的傾向。
通量小於零 (通量 < 0) 代表有向內匯集的傾向。
在以上的定義當中,曲面 S 並沒有要求是封閉的 (像汽球一樣),但是假如 S 是一個封閉曲面,那麼我們通常會用以下的環狀積分來代表這種封閉的情況。
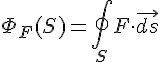
對於電場而言,通常我們在意的是環狀曲面的通量,因此可以用上述環狀積分符號 來表示此種情況。
通量的概念不只適用於一個粒子產生的電場,而是任何的電場都可以適用的。例如以下是兩個粒子所產生的電場,其中圖 (a) 是兩個負電粒子所產生的電場,所以如果在兩者之外定義一個封閉曲面,那麼其電通量將會是這兩個粒子的負電量總合。
同樣的,如果是像圖 (b) 這樣一正一負的兩個粒子,那麼通過外部封閉曲面的電通量,將會因為正負相互抵消而變成零。
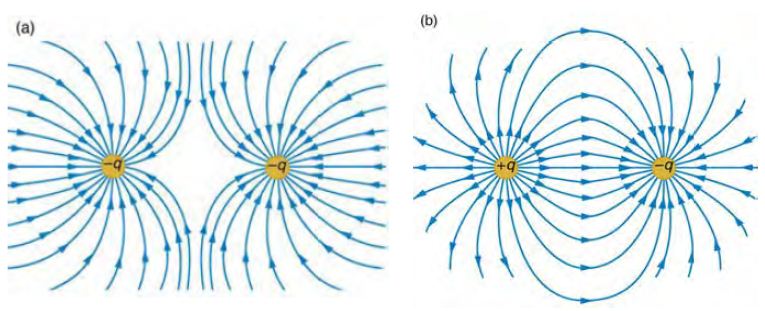
圖、兩個帶電粒子產生的電場與電通量
如果、我們想用微積分的概念,透過很多微小區塊的積分來計算通量總合的話,那麼我們就可以定義一個非常微小區域的通量密度,這種逼近無限小的平均通量概念,就稱為散度。其定義如下:
定義:散度
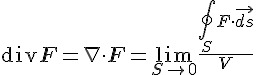
直覺意義:
F 是一個向量場 (例如電場),S 是一個封閉曲面,V 是封閉曲面所包圍的體積。
代表向量場與曲面法向量的內積。
代表封閉曲面 S 的通量。
散度是發散點或內聚點的衡量值。
發散點箭頭向外散射(散度 > 0)。
內聚點箭頭向內聚射 (散度 < 0)。
散度是單一點的通量密度。
如果某一點的散度大於 0,代表那個點向外射出的向量比向內射入的多,如果小於零則代表向內射入的向量比向外射出的多。
定理:散度定理,又稱「高斯散度定理」。

直覺意義:
V 是空間中的一個區域,而 S 是 V 的表面。
V 區域的散度積分
,等於向量場 F 對 S 的面積分
。
在電磁學中,這代表我們只要計算通過 S 曲面的向量積分
,就可以知道 V 區域裏面帶有多少電量。反過來說、只要知道 V 區域帶有多少電量,就知道通過其表面的電力線總共有多少。
散度定理的證明想法:對於曲面內部的兩個相鄰小立方體 A, B 而言,這些向量直接穿過相鄰面,所以從 A 射出的向量與 B 射入的向量互相抵消,因此只有最外圍的那一面才不會被抵銷,因此只要算最外層表面的向量加總就可以了。
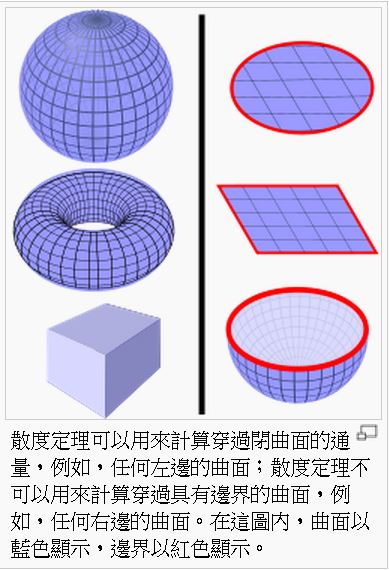
圖、散度定理的意義
所以散度定理只適用於封閉曲面 (如上圖左半邊的情況),但對於開放曲面 (如上圖右半邊的情況) 則不適用。
在迪卡兒座標系統內的通量與散度
在迪卡兒座標系統內,我們可以用下列函數來描述一個向量場
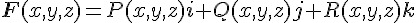
上式代表空間中的每一個點 (x,y,z) 都有一個向量 P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k 附著於該點上,其中的 i,j,k 分別是 x 軸、y 軸、z 軸方向上的單位向量,也就是 i=(1,0,0), j=(0,1,0), k=(0,0,1)。
那麼、所謂的某一個點的散度,在三維迪卡兒座標系統 (直角坐標系統) 內其實是向量場 F 在 (x,y,z) 這點的三個偏微分值加總。
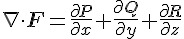
換句話說,在三維迪卡兒座標系統內,以下等式是成立的:
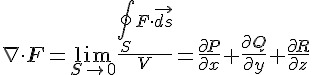
由於上式看起來等號兩邊並沒有直接關係,因此讀者必然感到奇怪,但是受限於筆者的數學能力,恐怕無法進行正式的證明,因此我們簡要的寫出「證明想法」如下。
證明想法:(非正式證明)
; 根據散度定義
; 根據下表的微量面積算式
; 根據均值定理,S 內部必然有個點
滿足此式
; 因為 S 無限小,所以
。
.
說明:上述陳述的證明想法,牽涉到「微量長度、微量面積、微量體積」的表示方法,如下所示:
| 微量極限 | 簡要概念 | 數學定義 |
|---|---|---|
| 微量體積 | 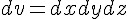 |
 |
| 微量長度 |  |
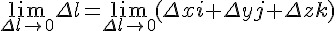 |
| 微量面積 | 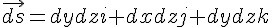 |
 |
注意:在迪卡兒座標系中,向量場 F 的散度為 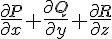 ,但這個算式其實是
,但這個算式其實是  的內積值,因此數學上才會用類似內積的
的內積值,因此數學上才會用類似內積的 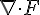 符號代表散度。
符號代表散度。
環量與旋度
環量與旋度是用來計算環繞著某個封閉曲線的旋轉力量強度,以下是一個環狀向量場的圖示範例:

圖、環形向量場
為了衡量向量場的這種旋轉強度,數學家們定義了環量這個概念。
定義:環量

直覺意義:
F 是一個向量場 (例如磁場),C 是一條封閉曲線,
是曲線邊緣的切線向量。
環量和通量一樣,是描述向量場的重要參數,但環量描述的是旋轉的力量總和,而通量描述的是吸引與排斥的力量總和。
某個區域中的環量不等於零,說明這個區域中的向量場表現出環繞某一點或某一區域旋轉的特性。
為了描述一個向量場 F 在一點附近的環量,將閉合曲線 C 收小,使它包圍面的面積 U 趨於零時,可以得到一個平均環量強度的極限值,這個平均環量強度就稱為該點的旋度。
定義:旋度
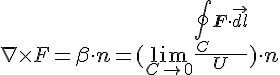
直覺意義:
F 是一個向量場 (例如磁場),C 是一條極小的封閉曲線,U 是 C 所包圍的面積大小。
旋度是環量範圍 C 趨近於零的結果,是某一點的環量除以面積的極限值 (環量密度)。
旋度代表被 C 包圍的那一點在方向
上的旋轉強度。
旋度與方向
有關,在不同的方向旋度也不同。
雖然旋度與散度一樣都是個純量,但是旋度卻必須指定方向  才有辦法計算,因此隨著方向
才有辦法計算,因此隨著方向  的不同,得到的旋度也會有所不同。
的不同,得到的旋度也會有所不同。
散度與旋度定理
定理:旋度定理、又稱「斯托克定理 (Stokes theorem)」
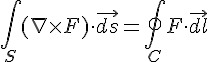
直覺意義:
S 是空間中的一個曲面,而 C 是環繞 S 邊緣的封閉曲線。
S 曲面上的旋度總和
,等於S 邊緣任一封閉曲線 C 的線積分
。
斯托克定理的證明想法:在下圖中,S 曲面內方格的共用邊向量會互相抵消,於是只要計算延著邊緣環繞線 C 的向量內積總和 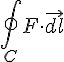 ,就可以算出整體的環量
,就可以算出整體的環量 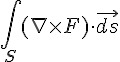 。
。
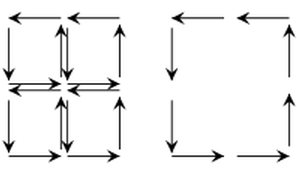
圖、斯托克定理 (Stokes theorem) 的適用情況
馬克斯威方程式
在電磁學上,有四個重要的物理量,分別是 - 電場 (E)、磁場 (H)、電通量 (D) 與磁通量 (B) 等,這四個物理量之間可形成四條重要的物理學關係式,這四條關係式便是著名的馬克斯威方程式。
以下是這四個物理量之間的關係式:
| 符號 | 對應的物理量 (四個符號均代表向量場) | 與其他符號間的關係式 |
|---|---|---|
| E | 電場強度 (Electric field intensity) | 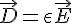 ; 其中 ; 其中  為介電率 為介電率 |
| H | 磁場強度 (Magnetic field intensity) | 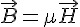 ; 其中 ; 其中 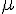 為導磁率 為導磁率 |
| D | 電通量密度 (Electric flux density) | 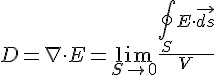 |
| B | 磁通量密度 (Magnetic flux density) | 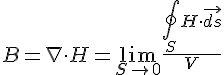 |
當初馬克斯威寫下的方程式,由於沒有使用「散度」與「旋度」這樣的算子,因此描述起來較為複雜,每個方程式都會寫成一組包含好幾個微分方程式的複雜寫法。但是有了上述的數學概念之後,我們就可以用「散度」與「旋度」這樣的算子,更簡單的描述馬克斯威方程式了。
以下是使用散度與旋度描述的馬克斯威方程式。
| 定律 | 微觀公式 (使用散度、旋度) | 巨觀公式 (使用通量、環量) | 說明 |
|---|---|---|---|
| 法拉第定律 |  |
 |
磁通量 B 的變化會產生感應電場 E |
| 安培定律 | 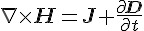 |
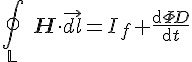 |
電流 J 與電通量變化  會產生磁場 H 會產生磁場 H |
| 高斯定律 | 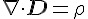 |
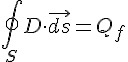 |
電荷密度  決定電通量 D 決定電通量 D |
| 自然定律 | 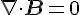 |
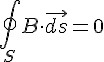 |
進入任一區域的磁通量一定等於出去的磁通量 |
如果是在相同的介質當中,上述方程式裏的介電率  與導磁率
與導磁率 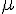 就會是固定的,此時整個馬克斯威方程式就可以進一步簡化為下列兩條:
就會是固定的,此時整個馬克斯威方程式就可以進一步簡化為下列兩條:
| 定律 | 公式 | 說明 |
|---|---|---|
| 法拉第定律 | 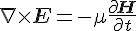 |
磁場強度 H 的變化會產生感應電場 E |
| 安培定律 | 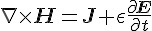 |
電流 J 與電場強度 E 的變化  會產生磁場 H 會產生磁場 H |
於是「法拉第定律」與「安培定律」就成了電磁學裏最重要的兩條方程式。
如果將上述相同介質中「法拉第定律」的「散度」與「旋度」等算子 (  ,
, 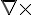 ) 給還原,然後再將每個方向的分量都寫出來,那麼上述的
) 給還原,然後再將每個方向的分量都寫出來,那麼上述的 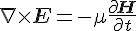 算式就可以改寫為下列向量場方程式:
算式就可以改寫為下列向量場方程式:
同樣的、安培定律 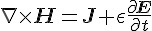 也可以改寫為以下的向量場方程式:
也可以改寫為以下的向量場方程式:
而上述的這種寫法也就是當初「馬克斯威」所寫的方程式形態,這種型態的方程式經過「黑維塞」用 (  ,
, 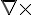 ) 等算子重新詮釋之後,就成了表格中您所看到的簡潔版本了。
) 等算子重新詮釋之後,就成了表格中您所看到的簡潔版本了。
根據上述的馬克斯威方程組,我們可以看到介電率和磁導率是兩個重要的常數,通常介電率用符號  表示,而磁導率 用符號
表示,而磁導率 用符號 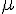 表示。
表示。
介電率是介質響應外加電場的極化的衡量值,介電率的測量單位是法拉/公尺(Farad/meter,F/m)。真空狀態的介電率 (「真空介電常數」) 的數值是 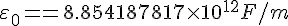
磁導率是一種材料對一個外加磁場線性反應的磁化程度。磁導率 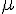 的單位是亨利每米(H/m),或牛頓每安培的平方(
的單位是亨利每米(H/m),或牛頓每安培的平方( 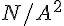 )。而真空狀態的磁導率為
)。而真空狀態的磁導率為  。
。
波動方程式
以下的向量場微分方程式可以用來描述電磁波的傳遞行為,因此稱為波動方程式 (其中的 E 代表電場,是個向量場)。
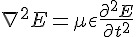
根據上述的波動方程式 ,電磁波的速度為 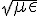 ,在真空狀態下,電磁波的速度等於
,在真空狀態下,電磁波的速度等於 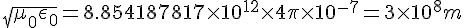 ,也就是光速,這個現象讓馬克斯威直覺的推論出「光是一種電磁波」。
,也就是光速,這個現象讓馬克斯威直覺的推論出「光是一種電磁波」。
那麼、波動方程式是怎麼來的呢?
這個問題的解答,當然是從馬克斯威方程延伸推論而來的,我們只要利用相同介值中的法拉第定律與安培定律,也就是下列兩條,就可以導出波動方程式了。
| 定律 | 公式 | 說明 |
|---|---|---|
| 法拉第定律 | 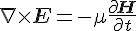 |
磁場強度 H 的變化會產生感應電場 E |
| 安培定律 | 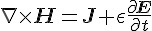 |
電流 J 與電場強度 E 的變化  會產生磁場 H 會產生磁場 H |
推導:波動方程式
根據上述的法拉第定律與安培定律,可推得下列結果
;
接著假設電流密度為零
,於是得到
;
接著根據迪卡兒座標系統中的 curl of curl 定理
,可得下式
;
接著假設電荷密度為零
,那麼根據
可推論
,於是得到:
; 這就是波動方程式了。
接著、我們就可以根據波動方程式推論電磁波的傳遞速度,讓我們用一個範例來看看這個推論:
範例:假設電場 E = P(x,y,z) i + Q(x,y,z) j + R(x,y,z) k ,其中
,而 Q, R 均為 0,那麼那麼請問 c 是多少才會符合波動方程式的解。
解答:
;
;
;
接著根據波動方程式
,可以得到下式:
;
所以可以推論
.
因此、上述範例中的電場之函數如下:
;
.
這代表 E 為一個往 z 軸方向行進的電磁波,其振幅為 A,而頻率為 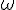 ,且行進速度為
,且行進速度為 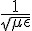 。
。
說明:上述電場波動的振幅為 A,頻率為 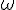 是比較容易理解的,學過 sin, cos 等三角函數的人應該可以輕易理解。 但是為何行進速度為
是比較容易理解的,學過 sin, cos 等三角函數的人應該可以輕易理解。 但是為何行進速度為 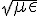 呢?
呢?
如果您想像一個海浪,正往右方打去,那麼該海浪的速度為多少呢?一個直覺的看法是看波峰走的距離,然後除以花費的時間就得到速度。
同樣的,對於 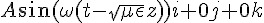 這個波而言,如果在 t 時間波峰在 z,且在 t+dt 這個時間點波峰在 z+dz,那麼我們就可以用 dz/dt 來計算波速。而要保持某點在正弦波上的位置不變,方法就是用
這個波而言,如果在 t 時間波峰在 z,且在 t+dt 這個時間點波峰在 z+dz,那麼我們就可以用 dz/dt 來計算波速。而要保持某點在正弦波上的位置不變,方法就是用 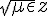 去抵銷 t 所造成的功效,也就是兩者都在波峰、或者兩者都在波谷的情況。
去抵銷 t 所造成的功效,也就是兩者都在波峰、或者兩者都在波谷的情況。
因此該電磁波的速度就是滿足 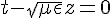 的情況,於是我們可以得到:
的情況,於是我們可以得到:
; 在某個時間 t,位置 z 處的電場大小為
; 在經過 dt 時間後,我們希望看到那個同樣大小的
向量移動到 z+dz。
; 也就是該電場大小不變,但是位置從 z 移到了 z+dz。
; 於是我們找出 dt 與 dz 的關係式。
; 也就是速度為
.
而且、我們知道在真空中,介電率 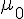 與
與 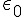 代入後,該速度
代入後,該速度 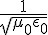 恰好為光速, 這也正是馬克斯威推論光波為一種電磁波的原因。
恰好為光速, 這也正是馬克斯威推論光波為一種電磁波的原因。
參考文獻
- College Physics, OpenStax College.
- Wikipedia:James Clerk Maxwell
- 維基百科:馬克士威方程組
- 維基百科:詹姆斯·克拉克·馬克士威
- 維基百科:論法拉第力線
- 維基百科:論物理力線
- 維基百科:電磁場的動力學理論
- 維基百科:麥克斯韋關係式
- 維基百科:旋度
- 維基百科:散度
- 維基百科:電容率
- 維基百科:磁導率
- 線代啟示錄:梯度、旋度與散度
【本文由陳鍾誠取材並修改自 維基百科 與 OpenStax College 的 College Physics 一書,採用創作共用的 姓名標示、相同方式分享 授權】
程式人文集
Arduino入門教學(11) – 多台 Arduino 間的通訊 - 透過 I2C (作者:Cooper Maa)
今天我們要介紹怎麼讓多台 Arduino 互相通訊。我們所用的通訊協定是 I2C Protocol,I2C 只需要兩支腳位就可以讓設備建立通訊,這兩支腳位一個叫作 SDA (Serial DAta line),另一個叫作 SCL (Serial CLock Line)。在大部份的 Arduino 板子上,SDA 是在 analog pin 4,而 SCL 是在 analog pin 5。
接線
參考底下的接線圖連接你的 Arduino:
接線方法很簡單,你只要把每一台 Arduino 的 SDA (analog pin 4), SCL (analog pin 5), GND 和 5V 分別連接在一起就可以了。另外,最好在 SDA 和 SCL 上加個接到 5V 的 4.7K 歐姆提升電阻以確保預設電壓為高電位。
I2C 是 Master-Slave 的架構,Master 可以向 Slave 發出需求要資料或傳送資料。I2C bus 上最多可以有 128 個設備。在 I2C bus 上可以有多個 Master 和多個 Slave,不過為了避免複雜,通常我們只會用一個 Master。每個 Slave 都會有一個識別的號碼,叫作 Slave address,Master 要跟 Slave 通訊的時候,就利用 Slave address 指定要跟哪個 Slave 建立對話。
底下將示範怎麼讓兩台 Arduino 透過 I2C 建立通訊。這兩台 Arduino 一台是 Master,一台是 Slave,其中 Slave 所用的 address 為 1。
程式
底下是 Master 的程式:
// master_sender.ino
// Refer to the "slave_receiver" example for use with this
#include <Wire.h>
const int SLAVE_ADDRESS = 1;
char incomingByte = 0;
void setup() {
Wire.begin(); // join I2C bus as a Master
Serial.begin(9600);
Serial.println("Type something to send:");
}
void loop() {
}
void serialEvent()
{
// read one byte from serial port
incomingByte = Serial.read();
// send the received data to slave
Wire.beginTransmission(SLAVE_ADDRESS);
Wire.write(incomingByte);
Wire.endTransmission();
}程式說明:
- Master 使用 Wire.begin() 加入 I2C bus
- 當 serial port 上有收到資料時,Arduino 會自動執行 serialEvent()。
- 在 serialEvent() 函式中,Master 首先會從 serial port 讀取一個 byte 的資料,然後再利用底下三行程式將資料透過 I2C 送給 Slave 1。
- 每當 Master 要送資料給 Slave 的時候,要先呼叫 Wire.beginTransmission() 建立傳輸,緊接著呼叫 Wire.write() 把資料放到 buffer,最後呼叫 Wire.endTransmission() 真正送出資料並結束傳輸。
// send the received data to slave
Wire.beginTransmission(SLAVE_ADDRESS);
Wire.write(incomingByte);
Wire.endTransmission();底下則是 Slave 的程式:
// slave_receiver.ino
// Refer to the "master_sender" example for use with this
#include <Wire.h>
const int SLAVE_ADDRESS = 1;
char incomingByte = 0;
void setup() {
Wire.begin(SLAVE_ADDRESS); // join I2C bus as a slave with address 1
Wire.onReceive(receiveEvent); // register event
Serial.begin(9600);
Serial.println("Received data:");
}
void loop() {
}
void receiveEvent(int howMany)
{
while (Wire.available())
{
// receive one byte from Master
incomingByte = Wire.read();
Serial.print(incomingByte);
}
}程式說明:
- Slave 一樣是使用 Wire.begin() 加入 I2C bus,但是必須傳入一個參數指定所用的 address
- 利用 Wire.onReceive(receiveEvent) 註冊事件,之後當 Master 送資料給 Slave 時,Arduino 就會自動呼叫 receiveEvent()
- 在 receiveEvent() 中,程式的邏輯很簡單,只是利用 Wire.available() 檢查是否有資料,接著利用 Wire.read() 將資料出來再丟到 serial port 上。
執行結果
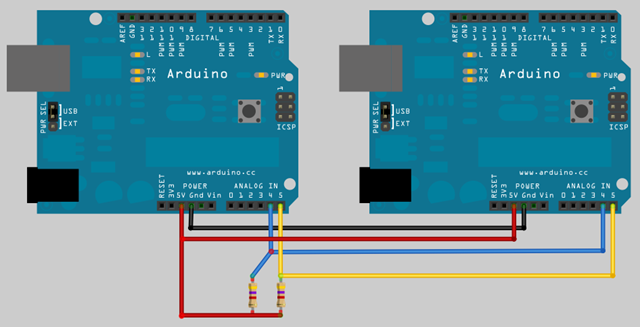
程式執行的時候,首先你會看到 Master 丟出一行 "Type something to send: " 的訊息。你可以在上面輸入任何資料,例如:
▲ 由於 Arduino IDE 不能同時開兩個 Serial Monitor,所以我用 Tera Term 開啟跟 Master 的連線
這時候 Slave 端就會顯示從 Master 端收到的資料,如下:
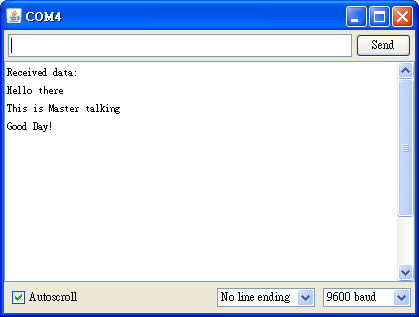
注意,在使用 Tera Term 的時候,記得要先設定 Terminal,這樣才可以看得到你輸入的資料而且 Tera Term 才會正確換行:
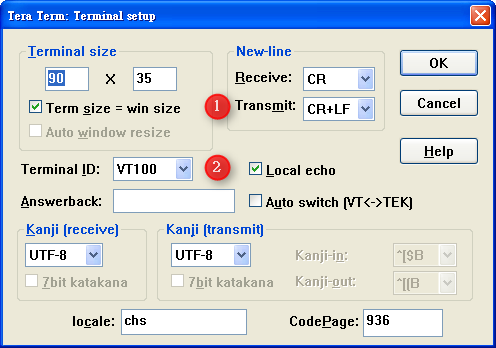
▲ 記得到 Setup > Terminal 畫面把 Transmit 改成 CR+LF 並把 Local echo 打開
參考資料
- I2C-Bus Specification
- Wire Library
- Communication between multiple Arduinos
- Arduino 1.0 的 serialEvent 介紹
- Tera Term
- 多台 Arduino 間的通訊 - 透過 I2C #1
- 多台 Arduino 間的通訊 - 透過 I2C #2
- 多台 Arduino 間的通訊 - 透過 I2C #3
- 多台 Arduino 間的通訊 - 透過 I2C #4
- EasyTransfer Library for Arduino
- EasyTransfer over I2C bus
【本文作者為馬萬圳,原文網址為: http://coopermaa2nd.blogspot.tw/2011/12/arduino-i2c.html ,由陳鍾誠編輯後納入本雜誌】
JavaScript (11) – 英文單字測驗程式 (作者:陳鍾誠)
在前兩期的「程式人雜誌」當中,我們介紹了的語音合成與辨識的主題,讓網頁也能做語音輸入或念出文章的動作,網址如下:
簡介
在本期中,我們將利用 Google 的語音合成功能,製作一個簡單的測驗程式,這個程式會隨機的抽取題目出來,然後製作出考題來測驗使用者。
由於運用了 Google 語音功能,可以讓使用者按下發音鈕聽英文發音,因此還沒學會拼字的小學生也可以用這個程式來學習英文。
此系統會自動累計計算您所答對與答錯的題目數量,透過這個程式,您可以測驗某人是否已經熟悉一群單字,這很適合用來考英文單字,我都用這個系統來考自己的小孩,看看他們英文單字是否背熟了。
為了鼓勵我的小孩使用這個程式,如果他們回答十題後,錯誤在一題之內的話,我就讓他們玩五分鐘的電動,我發現這樣學英文 還蠻方便的。
以下是這個「英文單字測驗程式」的介面,每次該程式都會隨機從「測驗題庫」中抽一組題目出來,然後再隨機產生四組答案 (不可與題目的答案重複) 當作候選項,接著用標準答案從剛剛產生的四組答案中隨機取代一組,如此四組答案當中必然有一個正確答案,以下是該程式的一個出題畫面。
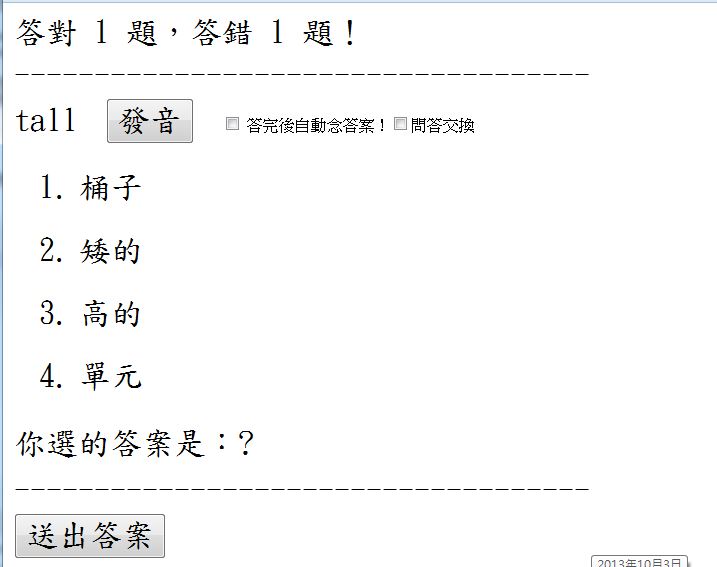
圖、英文單字測驗程式 - 測驗時
當測驗者選取答案並按下送出後,如果答錯了,系統會告訴您正確答案,請您更正。如果答對了,則系統將會讓您進到下一題,同時計算答對與答錯的題數。 以下是一個答錯時系統要求更正的畫面。

圖、英文單字測驗程式 - 答錯時
如果您在發音按鈕上按一下,則系統會使用 Google 語音合成 API 念出題目上的詞彙,這個功能對剛學英文的小孩特別有用,因為他們還不是很會拼字, 但是聽得懂發音,因此可以根據發音去猜測答案。
如果您在「答完後自動念答案!」這個選項上打勾,那麼當您答完之後,系統將念出整個正確答案。另外、如果您勾選「問答交換」這個選項,那麼 原本的「看英文、答中文」的功能,會切換成「看中文、答英文」的功能,如下所示:

圖、英文單字測驗程式 - 問答交換
使用影片
我已經將這個程式放在自己的 dropbox 網站當中,您可以點選下列網址來「用用看」這個程式,應該會更瞭解整個程式的運作過程。
或者您可以先看看我自己使用這個程式的一段教學錄影,先瞭解這個程式的操作方法,然後再自行操做看看:
程式原始碼
以下是這個程式的完整原始碼,您也可以剪貼後存放在自己電腦中使用,請記得要存成 UTF-8 格式。
檔案:english.html
<html>
<head>
<meta charset="utf-8" />
<style>
label, li, input { font-size:200%; font-family:標楷體; }
li { margin:25px 25px 25px 25px; }
a:hover { color:red; }
</style>
<style id="showboxstyle">
</style>
<script type="text/javascript">
var qaStr= "zero=零, one=一, two=二, three=三, four=四, five=五, six=六, seven=七, eight=八, nine=九, ten=十, eleven=十一, twelve=十二, thirteen=十三, fourteen=十四, fifteen=十五, sixteen=十六, seventeen=十七, eighteen=十八, nineteen=十九, twenty=二十, thirty=三十, forty=四十, fifty=五十, sixty=六十, seventy=七十, eighty=八十, ninety=九十, houndred=百, thousand=千, million=百萬, billion=十億, year=年, I=我, you=你, he=他(男生), she=她(女生), old=老;年齡大, read=讀, trace=描繪;跟著劃, unit=單元, how=如何, tall=高的, short=矮的, content=內容, write=寫, practice=練習, worksheet=工作清單, sentence=句子, learn=學習, new=新的, word=單字;詞彙, daily=每天的, count=數;算, repeat=重複, after=在...之後, sorrt=對不起, bad=壞的, father;dad=爹地;爸爸, bat=球棒, cat=貓, rat=老鼠, mad=生氣;抓狂, fat=胖的, bed=床, chair=椅子, desk=書桌, sofa=沙發, table=桌子, is;are;was;were=是, it=它, my=我的, no=不, on=在...上面, the=這個, under=在..下面, where=在哪裡, bag=袋子, key=鑰匙, pencil=鉛筆, box=盒子, watch=手錶, bottle=水壺, not=不, that=那個, this=這個, yes=是, your=你的, dig=挖, dot=小圓點, tip=小費;頂端, tub=桶子, zip=拉鏈, sip=吸, sit=坐, zoo=動物園, sad=傷心的;難過的, gap=間隔;間隙, cap=鴨舌帽, get=得到, cop=警察, god=上帝;神, cut=切;割, web=蜘蛛網, wet=濕的, hit=打擊, wit=機智, hop=單腳跳";
var qa = qaStr.split(",");
function rand(n) {
return Math.floor(Math.random()*n)
}
function selectQA() {
return qa[rand(qa.length)];
}
function Q(s) {
if (isSwap.checked)
return s.split("=")[1];
else
return s.split("=")[0];
}
function A(s) {
if (isSwap.checked)
return s.split("=")[0];
else
return s.split("=")[1];
}
var question=null, answers=[], choice=null, q=null, msg=null;
var audioControlQ = null, audioControlA = null, audioErrorControl=null, audioCorrectControl=null;
var correct=0, wrong=0, isChecked = false;
function load() {
question = document.getElementById("question");
answers = [];
answers[1] = document.getElementById("answer1");
answers[2] = document.getElementById("answer2");
answers[3] = document.getElementById("answer3");
answers[4] = document.getElementById("answer4");
choice = document.getElementById("choice");
msg = document.getElementById("msg");
countMag = document.getElementById("countMsg");
isAudio = document.getElementById("isAudio");
isSwap = document.getElementById("isSwap");
audioControlQ = document.getElementById("audio");
audioControlQ.addEventListener('ended', function(){ this.currentTime = 0; }, false);
audioControlA = document.getElementById("audio_zh");
audioControlA.addEventListener('ended', function(){ this.currentTime = 0; }, false);
audioErrorControl = document.getElementById("audio_error");
audioErrorControl.addEventListener('ended', function(){ this.currentTime = 0; }, false);
audioCorrectControl = document.getElementById("audio_error");
audioCorrectControl.addEventListener('ended', function(){ this.currentTime = 0; }, false);
}
function chooseA(obj) {
choice.innerHTML = obj.innerHTML;
}
function test() {
isChecked = false;
choice.innerHTML = "?";
msg.innerHTML = "";
q = selectQA();
question.innerHTML = Q(q);
answer = A(q);
if (isSwap.checked) {
audioControlQ.src = 'http://translate.google.com/translate_tts?ie=utf-8&tl=zh&q='+Q(q);
audioControlA.src = 'http://translate.google.com/translate_tts?ie=utf-8&tl=en&q='+A(q);
}
else {
audioControlQ.src = 'http://translate.google.com/translate_tts?ie=utf-8&tl=en&q='+Q(q);
audioControlA.src = 'http://translate.google.com/translate_tts?ie=utf-8&tl=zh&q='+A(q);
}
var set = {};
set[q] = "";
for (i=1; i<=4; ) {
a = selectQA();
answers[i].innerHTML = A(a);
if (set[a] == "") continue; else i++;
set[a] = "";
}
answers[1+rand(4)].innerHTML = A(q);
}
function check() {
if (isAudio.checked) {
if (choice.innerHTML != A(q)) {
setTimeout(function () {
playAudio('audio_error');
}, 1000);
} else {
setTimeout(function () {
playAudio('audio_correct');
}, 1000);
}
setTimeout(function () {
playAudio('audio');
}, 3000);
setTimeout(function () {
playAudio('audio_zh');
}, 4000);
}
if (isChecked) return (choice.innerHTML == A(q));
isChecked = true;
if (choice.innerHTML == A(q)) {
msg.innerHTML = "答對了!"+Q(q)+"="+A(q);
correct ++;
} else {
msg.innerHTML = "答錯了!"+Q(q)+"="+A(q)+",請更正!";
wrong ++;
}
countMsg.innerHTML = "答對 "+correct+" 題,答錯 "+wrong+" 題!";
return (choice.innerHTML == A(q));
}
function pass() {
if (check()) {
if (isAudio.checked)
passDelay = 6000;
else
passDelay = 0;
setTimeout(function () {
test();
}, passDelay);
}
}
function playAudio(name) {
document.getElementById(name).play();
}
</script>
</head>
<body onload="load(); test()">
<form>
<table width="95%">
<tr><td><label id="countMsg">答對 0 題,答錯 0 題!</label></tr>
<tr><td><label>------------------------------------</label></tr>
<tr><td>
<label id="question">詞彙</label>
<audio id="audio_correct" src="http://translate.google.com/translate_tts?ie=utf-8&tl=zh&q=答對了"></audio>
<audio id="audio_error" src="http://translate.google.com/translate_tts?ie=utf-8&tl=zh&q=答錯了"></audio>
<audio id="audio" src="http://translate.google.com/translate_tts?ie=utf-8&tl=en&q=mother"></audio>
<audio id="audio_zh" src="http://translate.google.com/translate_tts?ie=utf-8&tl=zh&q=媽媽"></audio>
<input type="button" onclick="playAudio('audio')" value="發音">
<input type="checkbox" id="isAudio"> 答完後自動念答案!<input type="checkbox" id="isSwap" onchange="test()">問答交換
<ol>
<li><a id="answer1" onclick="chooseA(this)">答案1</a></li>
<li><a id="answer2" onclick="chooseA(this)">答案2</a></li>
<li><a id="answer3" onclick="chooseA(this)">答案3</a></li>
<li><a id="answer4" onclick="chooseA(this)">答案4</a></li>
</ol>
</td></tr>
<tr><td><label>你選的答案是:</label><label id="choice">?</label></td></tr>
<tr><td><label id="msg">正確的答案是:?</label></td></tr>
<tr><td><label>------------------------------------</label></tr>
<tr><td>
<input type="button" value="送出答案" onclick="pass()"/><br/>
</td></tr>
</table>
</form>
</body>
</html>結語
透過 Google 語音 API,我們可以很容易的將發音功能或語音辨識功能加入到網頁中,這樣的功能對於像上述的測驗系統來說特別有用,這樣的網路服務大大的提升了網頁 JavaScript 程式設計人員的開發速度,讓建構這類的網站更加容易了。
從今年一月開始,本系列關於 JavaScript 的文章到此已經刊載了 11 期,到此將暫時告一個段落,日後筆者若還有關於 JavaScript 的文章,也還會不定期與讀者分享,感謝大家的閱讀!
參考文獻
R 統計軟體(8) – 變異數分析 (ANOVA) (作者:陳鍾誠)
簡介
在先前的兩篇文章中,我們曾經探討過「兩組樣本的平均值檢定」問題,以下是這兩篇文章的連結。
在上述第二篇文章中,當兩組樣本互相獨立時,我們可以透過檢定 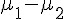 的信賴區間,採用 T 分布去檢定
的信賴區間,採用 T 分布去檢定 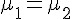 是否為真,這種方法稱為合併 T 檢定 (pooled T test),
是否為真,這種方法稱為合併 T 檢定 (pooled T test),
在此、先讓我們再次透過 R 軟體,進行一次 T 檢定,以便喚起讀者的記憶。
檢定兩樣本群的平均值是否相同
> x = rnorm(20, 5, 1)
> x
[1] 6.240855 4.229226 5.349843 6.023241 5.613232 5.300235 4.696128 5.452365
[9] 4.567735 5.260747 3.800322 6.168725 6.196059 4.969572 6.251078 3.549983
[17] 6.432844 5.308146 4.978811 4.944134
> y = rnorm(20, 5, 1)
> y
[1] 5.969639 5.400434 4.231995 4.804537 3.098015 5.481365 6.016810 2.769489
[9] 6.687201 4.240217 6.602660 4.777928 4.825274 4.110038 5.651073 5.829578
[17] 4.651262 6.036818 3.459562 5.993473
> t.test(x, y, var.equal=TRUE)
Two Sample t-test
data: x and y
t = 0.7519, df = 38, p-value = 0.4567
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.3973599 0.8669515
sample estimates:
mean of x mean of y
5.266664 5.031868
> z = rnorm(20, 4, 1)
> t.test(x, z, var.equal=TRUE)
Two Sample t-test
data: x and z
t = 5.9399, df = 38, p-value = 6.883e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1.079955 2.196671
sample estimates:
mean of x mean of y
5.266664 3.628351
> 在以上檢定中, x, y 兩者都是由 rnorm(20, 5, 1) 這個指令 (平均值 5,標準差為 1) 產生的樣本,所以檢定的結果 t.test(x, y, var.equal=TRUE) 之 p-value = 0.4567 ,由於該值遠大於 1-95% = 0.05,所以檢定結果無法否認虛無假設 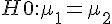 ,而且信賴區間為 (-0.3973599, 0.8669515) 包含
,而且信賴區間為 (-0.3973599, 0.8669515) 包含  ,這兩者都代表我們無法否認 H0。
,這兩者都代表我們無法否認 H0。
但是、在 t.test(x, z, var.equal=TRUE) 這個檢定中,由於 z 是 rnorm(20, 4, 1) 這個指令 (平均值 4,標準差為 1) 產生的樣本,檢定的結果 p-value = 6.883e-07 也遠小於 0.05,因此強力的否決了 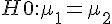 的可能性, 這點從信賴區間 (1.079955, 2.196671) 不包含 0 這件事情上,也可以清楚的看到。
的可能性, 這點從信賴區間 (1.079955, 2.196671) 不包含 0 這件事情上,也可以清楚的看到。
變異數分析 (Analysis of Variance, ANOVA)
但是、如果樣本群的數目變多了,不是兩組樣本,而是 k 組樣本的話,事情就會變得比較麻煩!
如果要用上述的合併 T 檢定對 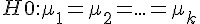 中的每個配對都作檢定,那麼就要對 (1, 2), (1, 3), ... (1, k), (2, 3), (2,4), ... (2, k), .... (k-1, k) 等
中的每個配對都作檢定,那麼就要對 (1, 2), (1, 3), ... (1, k), (2, 3), (2,4), ... (2, k), .... (k-1, k) 等  種配對都進行一次檢定,這樣的方式有點太麻煩了。
種配對都進行一次檢定,這樣的方式有點太麻煩了。
此時、我們可以採用變異數分析 (中國大陸稱為方差分析) 的方法,來檢定假設 H0 是否成立,也就是檢驗是否所有樣本群的平均值都相同。
讓我們暫時不去探討背後的數學,直接用 R 軟體進行一次變異數分析的檢定,看看這種檢定是如何進行的,以下是一個簡單的操作過程。
> X = rnorm(40, 5, 1) # 產生四十個樣本 (平均值 5,標準差 1)
> X
[1] 5.584603 4.052913 4.434469 5.844309 5.286695 5.188169 4.796683 3.913132
[9] 5.467150 5.740397 4.528423 4.395270 4.994147 4.014513 6.259213 6.898331
[17] 3.792135 3.879688 5.334643 5.887895 5.647250 5.603816 5.465186 6.703394
[25] 5.153999 4.855386 2.129850 5.477026 4.785934 4.138114 5.726216 3.581281
[33] 5.255695 4.515353 6.391714 3.726963 5.744328 5.314164 4.647955 4.848313
> A = factor(rep(1:4, each=10)) # 產生標記 1, 2, 3, 4 各 10 份
> A
[1] 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4
[37] 4 4 4 4
> XA = data.frame(X, A) # 建立框架變數 XA,為每個 X 樣本分別標上 1, 2, 3, 4 等標記。
> aov.XA = aov(X~A, data=XA) # 進行「變異數分析」,看看 X 與 A 之間是否有相關。
> summary(aov.XA) # 印出「變異數分析」的結果報表
Df Sum Sq Mean Sq F value Pr(>F)
A 3 5.015 1.6718 2.119 0.115
Residuals 36 28.408 0.7891
> plot(XA$X~XA$A) # 繪出 X~A 的盒狀圖在上述操作中,我們用 X = rnorm(40, 5, 1) 產生四十個樣本,然後用 A = factor(rep(1:4, each=10)) 與 XA = data.frame(X, A) 這個指令將這四十個樣本分為四群,每群 10 個,分別標以 1, 2, 3, 4 的標記,成為 XA 這個框架 (frame) 變數,然後利用 `aov.XA = aov(X~A, data=XA)' 這個指令進行「變異數分析」,並用 summary(aov.XA) 指令印出分析結果。
您可以看到在分析結果中,Pr(>F) = 0.115 ,並沒有低於 (1-95%) 的 0.05 範圍,因此各組的平均值間沒有明顯差異,我們無法否認 H0。
最後我們用 plot(XA$X~XA$A) 這個指令匯出盒狀圖,就可以大致看到四組分佈的情況。
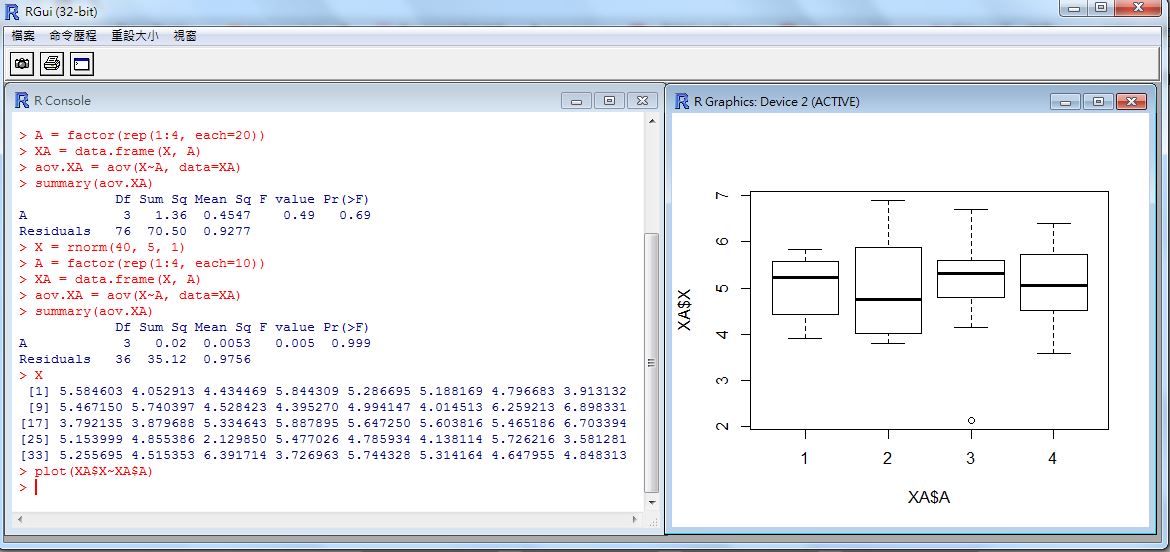
圖、X 與 A 之間關係的盒狀圖
但是、如果我們再用 rnorm(10, 4, 1) 這個指令產生一組樣本群加入上述資料 X 中,並將這組新產生的樣本群標示為編號 5 ,由於 此組新樣本群的母體平均值為 4 (而不是 5),因此應該會有明顯不同,以下是我們的實驗操作過程。
> Y = c(X, rnorm(10, 4, 1)) # 將 X 補上 10 個均值為 4 的隨機樣本,成為 Y
> Y
[1] 5.584603 4.052913 4.434469 5.844309 5.286695 5.188169 4.796683 3.913132
[9] 5.467150 5.740397 4.528423 4.395270 4.994147 4.014513 6.259213 6.898331
[17] 3.792135 3.879688 5.334643 5.887895 5.647250 5.603816 5.465186 6.703394
[25] 5.153999 4.855386 2.129850 5.477026 4.785934 4.138114 5.726216 3.581281
[33] 5.255695 4.515353 6.391714 3.726963 5.744328 5.314164 4.647955 4.848313
[41] 3.516310 4.174873 2.541251 2.851404 4.862902 2.739729 2.848565 3.169462
[49] 4.245488 3.543660
> B = c(A, rep(5, 10)) # 產生 10 個編號 5 的標號,將 A 擴充為 B,為新的 10 個樣本標號。
> B
[1] 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4
[37] 4 4 4 4 5 5 5 5 5 5 5 5 5 5
> YB = data.frame(Y, B) # 建立框架變數 YB,為 XA 補上 10 個新樣本的結果
> aov.YB = aov(Y~B, data=YB) # 進行「變異數分析」,看看 Y 與 B 之間是否有相關。
> summary(aov.YB) # 印出「變異數分析」的結果報表
Df Sum Sq Mean Sq F value Pr(>F)
B 1 10.15 10.152 9.84 0.00292 **
Residuals 48 49.52 1.032
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
> plot(YB$Y~YB$B) # 繪出 Y~B 的盒狀圖於是當我們用 aov.YB = aov(Y~B, data=YB) 這個指令去進行「變異數分析」時,就會發現 Pr(>F) 為 0.00292,遠低於 0.05,所以我們可以否認假設 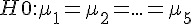 ,也就是認為應該至少有一樣本群與其他樣本群的平均值有顯著的不同。
,也就是認為應該至少有一樣本群與其他樣本群的平均值有顯著的不同。
以下是我們用上述 plot() 指令所繪出的結果,您可以發現第五群樣本明顯的偏低。
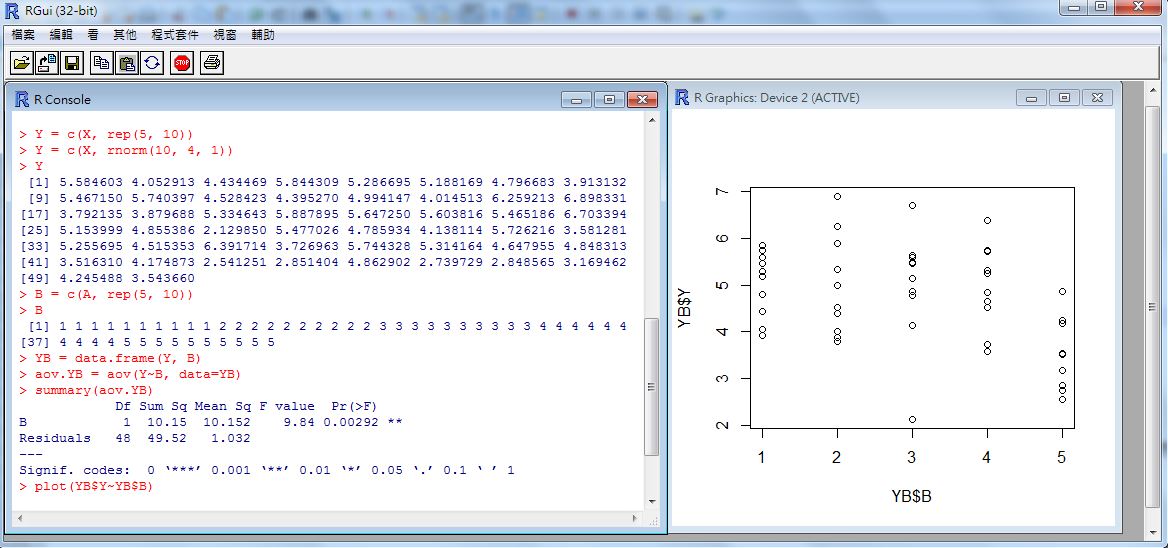
圖、Y 與 B 之間關係的盒狀圖
這也是為何 aov(Y~B, data=YB) 的結果會認為應該否認虛無假設 H0 的原因。
兩兩之間的均值比較
雖然在上述分析 Y~B 的過程當中,我們否認了 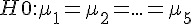 這個假設,但是從分析結果中卻無法得知到底哪一個樣本群有明顯的不同。
這個假設,但是從分析結果中卻無法得知到底哪一個樣本群有明顯的不同。
此時我們可以用 pairwise.t.test 這個函數,來比較兩兩間的不同,以下是我們的比較過程:
首先我們對 X~A 兩者之間進行兩兩比較,您可以看到下列結果。
> pairwise.t.test(X, A)
Pairwise comparisons using t tests with pooled SD
data: X and A
1 2 3
2 1 - -
3 1 1 -
4 1 1 1
P value adjustment method: holm 上述結果發現 (1, 2) (1,3), (1,4), (2,3), (2,4), (3,4) 之間是相同的,所以其矩陣內容值都是 1。
但是如果我們用 pairwise.t.test(Y, B) 指令來檢定 Y 與 B 之間的關係,那就會得到如下結果。
> pairwise.t.test(Y, B)
Pairwise comparisons using t tests with pooled SD
data: Y and B
1 2 3 4
2 1.0000 - - -
3 1.0000 1.0000 - -
4 1.0000 1.0000 1.0000 -
5 0.0053 0.0060 0.0060 0.0060
P value adjustment method: holm 從上述的結果中,您可以看到第 5 列的內容為「0.0053 0.0060 0.0060 0.0060」,明顯的較低,這代表第 5 列的平均值有顯著的不同。
不過、您看到的比較結果,是透過 holm 這個調整方法對顯著值 (P) 進行調整過的,如果沒有調整過,則 (X,A) 及 (Y,B) 的兩兩比較結果將會如下所示。
> pairwise.t.test(X, A, p.adjust.method="none")
Pairwise comparisons using t tests with pooled SD
data: X and A
1 2 3
2 0.94 - -
3 0.94 1.00 -
4 0.90 0.96 0.96
P value adjustment method: none
> pairwise.t.test(Y, B, p.adjust.method="none")
Pairwise comparisons using t tests with pooled SD
data: Y and B
1 2 3 4
2 0.93936 - - -
3 0.93482 0.99545 - -
4 0.89612 0.95654 0.96108 -
5 0.00053 0.00067 0.00068 0.00079
P value adjustment method: none 您仍然可以看到第 5 列的內容「0.00053 0.00067 0.00068 0.00079」明顯的較低,而且幾乎都低於 0.05,因此樣本群 5 的平均值明顯與其他四群有所不同。
結語
在以上的實驗中,我們可以透過 R 軟體中的「變異數分析」函數 aov() 進行多組樣本的平均值比較,瞭解這些樣本的母體平均值是否相同。
假如「變異數分析」的結果認為有所不同,那麼我們就可以利用 pairwise.t.test() 函數,去檢驗看看到底哪些群體之間有所不同,以便找出明顯不同的樣本群。
這種方法在很多「自然科學與社會科學」的實驗當中,都會是很有用的,例如我們可以用「變異數分析」來檢驗「幾種銷售方式之間」是否有明顯的差異,「幾種農藥的除草效果」間是否有明顯差異等等,這些分析對我們進行多組樣本的統計實驗可以提供很好的指引效果。
在本系列文章中,我們已經用 R 軟體介紹了主要的基礎統計方法,並將至此暫時畫下一個句點。日後筆者若還有關於 R 的文章,也還會不定期與讀者分享,感謝各位讀者的閱讀!
參考文獻
- R语言与统计分析, 作者: 汤银才, ISBN: 9787040250626。
Verilog (5) – 邊緣觸發正反器 (作者:陳鍾誠)
在本文中,我們將介紹如何用 Verilog 實作兩種概念,第一個是正反器 (Latch, Flip-Flop),第二個是脈波變化偵測器 (Pulse Transition Detector),然後再用這兩個元件組合成「邊緣觸發正反器」 (Edge Triggered Flip-Flop)。
正反器
正反器是可以用來儲存位元,是循序電路的基礎,以下是一個用 NAND 閘構成的正反器。
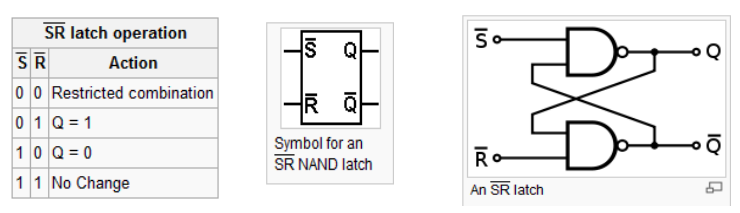
圖、NAND 閘構成的正反器
我們可以根據上圖實作出對應的 Verilog 程式如下:
檔案:latch.v
module latch(input Sbar, Rbar, output Q, Qbar);
nand LS(Q, Sbar, Qbar);
nand LR(Qbar, Rbar, Q);
endmodule
module main;
reg Sbar, Rbar;
wire Q, Qbar;
latch latch1(Sbar, Rbar, Q, Qbar);
initial
begin
$monitor("%4dns monitor: Sbar=%d Rbar=%d Q=%d Qbar=%d", $stime, Sbar, Rbar, Q, Qbar);
$dumpfile("latch.vcd"); // 輸出給 GTK wave 顯示波型
$dumpvars;
end
always #50 begin
Sbar = 0; Rbar = 1;
#50;
Sbar = 1; Rbar = 1;
#50;
Sbar = 1; Rbar = 0;
#50;
end
initial #500 $finish;
endmodule執行結果:
D:\verilog>iverilog -o latch latch.v
D:\verilog>vvp latch
VCD info: dumpfile latch.vcd opened for output.
0ns monitor: Sbar=x Rbar=x Q=x Qbar=x
50ns monitor: Sbar=0 Rbar=1 Q=1 Qbar=0
100ns monitor: Sbar=1 Rbar=1 Q=1 Qbar=0
150ns monitor: Sbar=1 Rbar=0 Q=0 Qbar=1
250ns monitor: Sbar=0 Rbar=1 Q=1 Qbar=0
300ns monitor: Sbar=1 Rbar=1 Q=1 Qbar=0
350ns monitor: Sbar=1 Rbar=0 Q=0 Qbar=1
450ns monitor: Sbar=0 Rbar=1 Q=1 Qbar=0
500ns monitor: Sbar=1 Rbar=1 Q=1 Qbar=0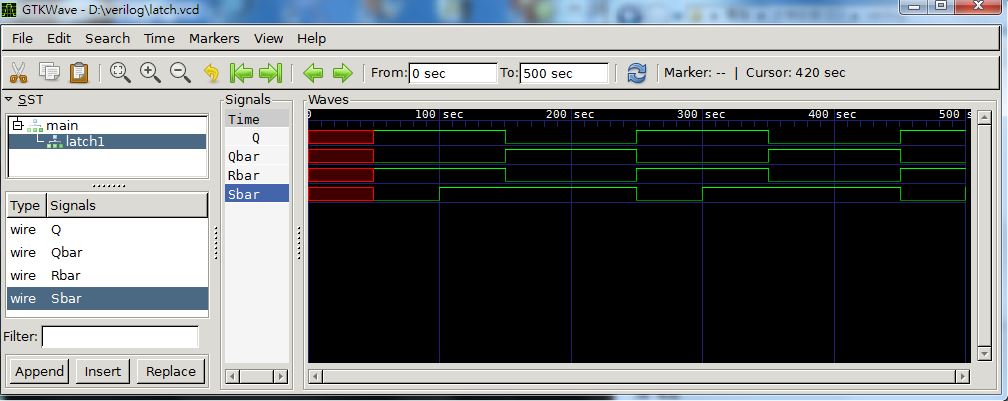
圖、latch.vcd 的顯示圖形
有 enable 的正反器
如果我們在上述正反器前面再加上兩個 NAND 閘進行控制,就可以形成一組有 enable 的正反器,以下是該正反器的圖形。
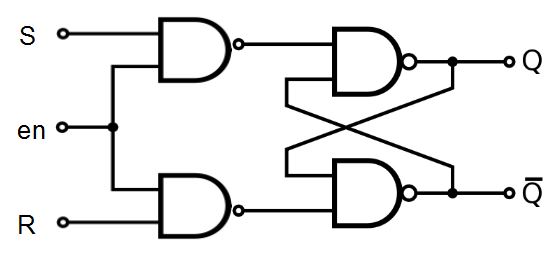
圖、有 enable 的正反器
根據上述圖形我們可以設計出以下的 Verilog 程式。
檔案:enLatch.v
module latch(input Sbar, Rbar, output Q, Qbar);
nand LS(Q, Sbar, Qbar);
nand LR(Qbar, Rbar, Q);
endmodule
module enLatch(input en, S, R, output Q, Qbar);
nand ES(Senbar, en, S);
nand ER(Renbar, en, R);
latch L1(Senbar, Renbar, Q, Qbar);
endmodule
module main;
reg S, en, R;
wire Q, Qbar;
enLatch enLatch1(en, S, R, Q, Qbar);
initial
begin
$monitor("%4dns monitor: en=%d S=%d R=%d Q=%d Qbar=%d", $stime, en, S, R, Q, Qbar);
$dumpfile("enLatch.vcd"); // 輸出給 GTK wave 顯示波型
$dumpvars;
end
always #50 begin
en = 1;
#50;
S = 1; R = 0;
#50;
S = 0; R = 0;
#50;
S = 0; R = 1;
#50
en = 0;
#50;
S = 1; R = 0;
#50;
S = 0; R = 0;
#50;
S = 0; R = 1;
end
initial #1000 $finish;
endmodule執行結果
D:\verilog>iverilog -o enLatch enLatch.v
D:\verilog>vvp enLatch
VCD info: dumpfile enLatch.vcd opened for output.
0ns monitor: en=x Sbar=x Rbar=x Q=x Qbar=x
50ns monitor: en=1 Sbar=x Rbar=x Q=x Qbar=x
100ns monitor: en=1 Sbar=1 Rbar=0 Q=1 Qbar=0
150ns monitor: en=1 Sbar=0 Rbar=0 Q=1 Qbar=0
200ns monitor: en=1 Sbar=0 Rbar=1 Q=0 Qbar=1
250ns monitor: en=0 Sbar=0 Rbar=1 Q=0 Qbar=1
300ns monitor: en=0 Sbar=1 Rbar=0 Q=0 Qbar=1
350ns monitor: en=0 Sbar=0 Rbar=0 Q=0 Qbar=1
400ns monitor: en=0 Sbar=0 Rbar=1 Q=0 Qbar=1
450ns monitor: en=1 Sbar=0 Rbar=1 Q=0 Qbar=1
500ns monitor: en=1 Sbar=1 Rbar=0 Q=1 Qbar=0
550ns monitor: en=1 Sbar=0 Rbar=0 Q=1 Qbar=0
600ns monitor: en=1 Sbar=0 Rbar=1 Q=0 Qbar=1
650ns monitor: en=0 Sbar=0 Rbar=1 Q=0 Qbar=1
700ns monitor: en=0 Sbar=1 Rbar=0 Q=0 Qbar=1
750ns monitor: en=0 Sbar=0 Rbar=0 Q=0 Qbar=1
800ns monitor: en=0 Sbar=0 Rbar=1 Q=0 Qbar=1
850ns monitor: en=1 Sbar=0 Rbar=1 Q=0 Qbar=1
900ns monitor: en=1 Sbar=1 Rbar=0 Q=1 Qbar=0
950ns monitor: en=1 Sbar=0 Rbar=0 Q=1 Qbar=0
1000ns monitor: en=1 Sbar=0 Rbar=1 Q=0 Qbar=1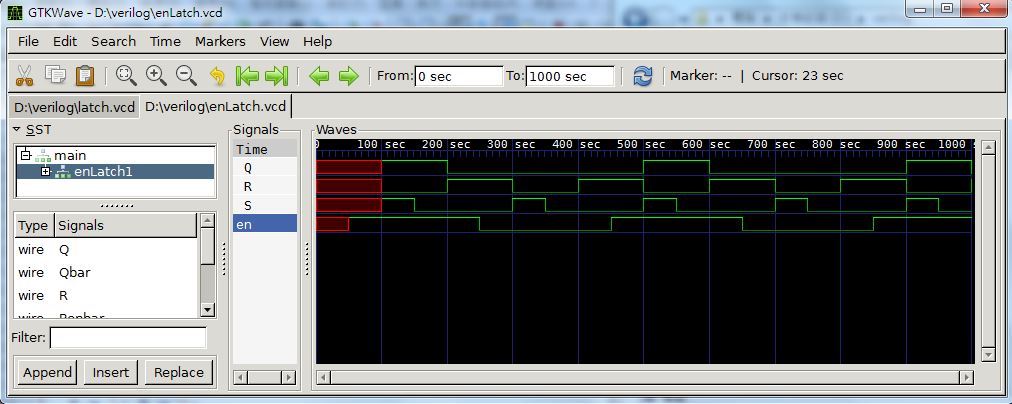
圖、enLatch.vcd 的顯示圖形
脈波變化偵測器 (Pulse Transition Detector, PTD)
傳統上,要做邊緣觸發的正反器,必須使用 Master-Slave 的架構,這樣要消耗較多的邏輯閘,但是現在通常改用 「脈波變化偵測電路」來偵測時脈的邊緣,這樣不僅可以簡化電路,而且適用性也更廣、更好用,因為任何需要偵測邊緣的地方都可以使用這樣的電路進行偵測。
以下是「脈波變化偵測電路」的圖形,其中的關鍵是在 左邊的 not 閘身上,由於每個閘都會造成延遲,因此多了 not 閘的那條路徑所造成的延遲較多,這讓輸出部份會因為延遲而形成一個脈衝波形。
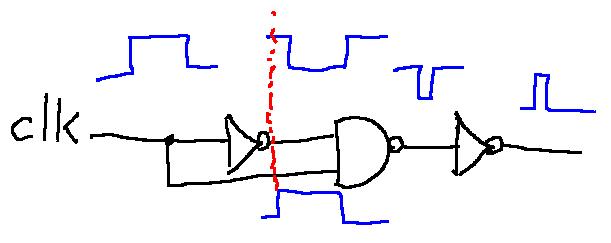
圖、脈波變化偵測器
以下是這個電路以 Verilog 實作的結果。
檔案:ptd.v
module ptd(input clk, output ppulse);
not #2 P1(nclkd, clk);
nand #2 P2(npulse, nclkd, clk);
not #2 P3(ppulse, npulse);
endmodule
module main;
reg clk;
wire p;
ptd ptd1(clk, p);
initial begin
clk = 0;
$monitor("%dns monitor: clk=%b p=%d", $stime, clk, p);
$dumpfile("ptd.vcd"); // 輸出給 GTK wave 顯示波型
$dumpvars;
end
always #50 begin
clk = clk + 1;
end
initial #500 $finish;
endmodule執行結果
D:\Dropbox\Public\pmag\201311\code>iverilog -o ptd ptd.v
D:\Dropbox\Public\pmag\201311\code>vvp ptd
VCD info: dumpfile ptd.vcd opened for output.
0ns monitor: clk=0 p=z
4ns monitor: clk=0 p=0
50ns monitor: clk=1 p=0
54ns monitor: clk=1 p=1
56ns monitor: clk=1 p=0
100ns monitor: clk=0 p=0
150ns monitor: clk=1 p=0
154ns monitor: clk=1 p=1
156ns monitor: clk=1 p=0
200ns monitor: clk=0 p=0
250ns monitor: clk=1 p=0
254ns monitor: clk=1 p=1
256ns monitor: clk=1 p=0
300ns monitor: clk=0 p=0
350ns monitor: clk=1 p=0
354ns monitor: clk=1 p=1
356ns monitor: clk=1 p=0
400ns monitor: clk=0 p=0
450ns monitor: clk=1 p=0
454ns monitor: clk=1 p=1
456ns monitor: clk=1 p=0
500ns monitor: clk=0 p=0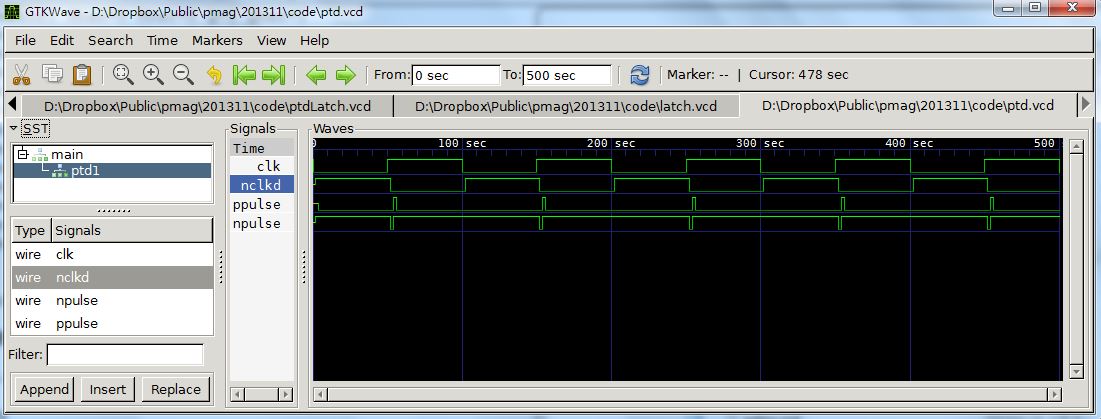
圖、ptd.vcd 的顯示圖形
邊緣觸發的正反器
有了「正反器」與「脈波變化偵測電路」之後,我們就可以組合出「邊緣觸發正反器」了,以下是其電路圖。
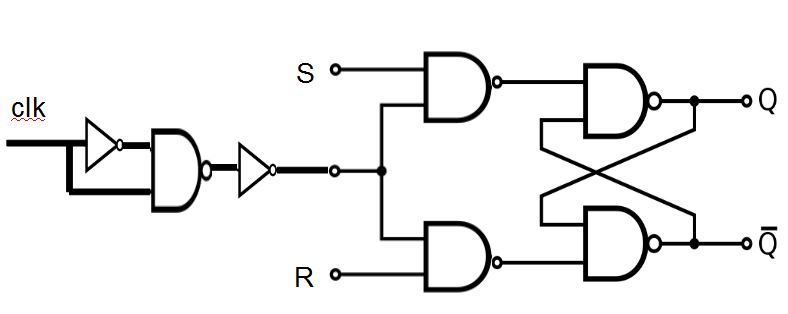
圖、邊緣觸發的正反器
事實上,上述電路圖只是將「有 enable 的正反器」前面加上一個「脈波變化偵測電路」而已,其實做的 Verilog 程式如下。
檔案:ptdLatch.v
module latch(input Sbar, Rbar, output Q, Qbar);
nand LS(Q, Sbar, Qbar);
nand LR(Qbar, Rbar, Q);
endmodule
module enLatch(input en, S, R, output Q, Qbar);
nand ES(Senbar, en, S);
nand ER(Renbar, en, R);
latch L1(Senbar, Renbar, Q, Qbar);
endmodule
module ptd(input clk, output ppulse);
not #2 P1(nclkd, clk);
nand #2 P2(npulse, nclkd, clk);
not #2 P3(ppulse, npulse);
endmodule
module ptdLatch(input clk, S, R, output Q, Qbar);
ptd PTD(clk, ppulse);
enLatch EL(ppulse, S, R, Q, Qbar);
endmodule
module main;
reg S, clk, R;
wire Q, Qbar;
ptdLatch ptdLatch1(clk, S, R, Q, Qbar);
initial
begin
clk = 0;
$monitor("%4dns monitor: clk=%d ppulse=%d S=%d R=%d Q=%d Qbar=%d", $stime, clk, ptdLatch1.ppulse, S, R, Q, Qbar);
$dumpfile("ptdLatch.vcd"); // 輸出給 GTK wave 顯示波型
$dumpvars;
end
always #20 begin
clk = ~clk;
end
always #50 begin
S = 1; R = 0;
#50;
S = 0; R = 0;
#50;
S = 0; R = 1;
#50;
end
initial #500 $finish;
endmodule執行結果
D:\verilog>iverilog -o ptdLatch ptdLatch.v
D:\verilog>vvp ptdLatch
VCD info: dumpfile ptdLatch.vcd opened for output.
0ns monitor: clk=0 ppulse=z S=x R=x Q=x Qbar=x
4ns monitor: clk=0 ppulse=0 S=x R=x Q=x Qbar=x
20ns monitor: clk=1 ppulse=0 S=x R=x Q=x Qbar=x
24ns monitor: clk=1 ppulse=1 S=x R=x Q=x Qbar=x
26ns monitor: clk=1 ppulse=0 S=x R=x Q=x Qbar=x
40ns monitor: clk=0 ppulse=0 S=x R=x Q=x Qbar=x
50ns monitor: clk=0 ppulse=0 S=1 R=0 Q=x Qbar=x
60ns monitor: clk=1 ppulse=0 S=1 R=0 Q=x Qbar=x
64ns monitor: clk=1 ppulse=1 S=1 R=0 Q=1 Qbar=0
66ns monitor: clk=1 ppulse=0 S=1 R=0 Q=1 Qbar=0
80ns monitor: clk=0 ppulse=0 S=1 R=0 Q=1 Qbar=0
100ns monitor: clk=1 ppulse=0 S=0 R=0 Q=1 Qbar=0
104ns monitor: clk=1 ppulse=1 S=0 R=0 Q=1 Qbar=0
106ns monitor: clk=1 ppulse=0 S=0 R=0 Q=1 Qbar=0
120ns monitor: clk=0 ppulse=0 S=0 R=0 Q=1 Qbar=0
140ns monitor: clk=1 ppulse=0 S=0 R=0 Q=1 Qbar=0
144ns monitor: clk=1 ppulse=1 S=0 R=0 Q=1 Qbar=0
146ns monitor: clk=1 ppulse=0 S=0 R=0 Q=1 Qbar=0
150ns monitor: clk=1 ppulse=0 S=0 R=1 Q=1 Qbar=0
160ns monitor: clk=0 ppulse=0 S=0 R=1 Q=1 Qbar=0
180ns monitor: clk=1 ppulse=0 S=0 R=1 Q=1 Qbar=0
184ns monitor: clk=1 ppulse=1 S=0 R=1 Q=0 Qbar=1
186ns monitor: clk=1 ppulse=0 S=0 R=1 Q=0 Qbar=1
200ns monitor: clk=0 ppulse=0 S=0 R=1 Q=0 Qbar=1
220ns monitor: clk=1 ppulse=0 S=0 R=1 Q=0 Qbar=1
224ns monitor: clk=1 ppulse=1 S=0 R=1 Q=0 Qbar=1
226ns monitor: clk=1 ppulse=0 S=0 R=1 Q=0 Qbar=1
240ns monitor: clk=0 ppulse=0 S=0 R=1 Q=0 Qbar=1
250ns monitor: clk=0 ppulse=0 S=1 R=0 Q=0 Qbar=1
260ns monitor: clk=1 ppulse=0 S=1 R=0 Q=0 Qbar=1
264ns monitor: clk=1 ppulse=1 S=1 R=0 Q=1 Qbar=0
266ns monitor: clk=1 ppulse=0 S=1 R=0 Q=1 Qbar=0
280ns monitor: clk=0 ppulse=0 S=1 R=0 Q=1 Qbar=0
300ns monitor: clk=1 ppulse=0 S=0 R=0 Q=1 Qbar=0
304ns monitor: clk=1 ppulse=1 S=0 R=0 Q=1 Qbar=0
306ns monitor: clk=1 ppulse=0 S=0 R=0 Q=1 Qbar=0
320ns monitor: clk=0 ppulse=0 S=0 R=0 Q=1 Qbar=0
340ns monitor: clk=1 ppulse=0 S=0 R=0 Q=1 Qbar=0
344ns monitor: clk=1 ppulse=1 S=0 R=0 Q=1 Qbar=0
346ns monitor: clk=1 ppulse=0 S=0 R=0 Q=1 Qbar=0
350ns monitor: clk=1 ppulse=0 S=0 R=1 Q=1 Qbar=0
360ns monitor: clk=0 ppulse=0 S=0 R=1 Q=1 Qbar=0
380ns monitor: clk=1 ppulse=0 S=0 R=1 Q=1 Qbar=0
384ns monitor: clk=1 ppulse=1 S=0 R=1 Q=0 Qbar=1
386ns monitor: clk=1 ppulse=0 S=0 R=1 Q=0 Qbar=1
400ns monitor: clk=0 ppulse=0 S=0 R=1 Q=0 Qbar=1
420ns monitor: clk=1 ppulse=0 S=0 R=1 Q=0 Qbar=1
424ns monitor: clk=1 ppulse=1 S=0 R=1 Q=0 Qbar=1
426ns monitor: clk=1 ppulse=0 S=0 R=1 Q=0 Qbar=1
440ns monitor: clk=0 ppulse=0 S=0 R=1 Q=0 Qbar=1
450ns monitor: clk=0 ppulse=0 S=1 R=0 Q=0 Qbar=1
460ns monitor: clk=1 ppulse=0 S=1 R=0 Q=0 Qbar=1
464ns monitor: clk=1 ppulse=1 S=1 R=0 Q=1 Qbar=0
466ns monitor: clk=1 ppulse=0 S=1 R=0 Q=1 Qbar=0
480ns monitor: clk=0 ppulse=0 S=1 R=0 Q=1 Qbar=0
500ns monitor: clk=1 ppulse=0 S=0 R=0 Q=1 Qbar=0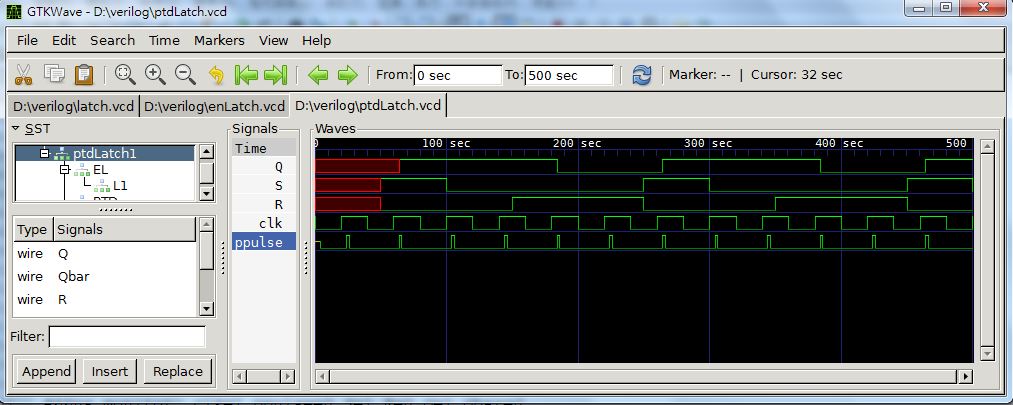
圖、ptdLatch.vcd 的顯示圖形
結語
有了「脈波變化偵測電路」,只要與任何需要偵測脈波變化的元件串接起來,就可以達到「邊緣觸發」的功能。
其實、像是 Verilog 當中的以下程式,其實都是利用類似的「脈波變化偵測電路」所完成的。
always @(posedge clock) begin
...
end參考文獻
【本文圖片修改自 維基百科,採用創作共用的 姓名標示、相同方式分享 授權】
開放電腦計畫 (5) – 支援完整指令集的 CPU0sc 處理器:使用 Verilog 實作 (作者:陳鍾誠)
簡介
在上一期當中,我們用 Verilog 設計了一個只有四個指令的簡化版處理器 CPU0mc.v ,文章網址如下:
如果您讀過上述文章,應該已經瞭解如何用 Verilog 設計簡單的指令與 CPU 了。在本文中,我們將延續 上期的主題,更深入的說明如何用 Verilog 設計出一顆具有完整指令集的處理器 -- CPU0sc.v 。
程式碼
我們只要將上期的 CPU0mc 繼續延伸,加入更多的指令實作,就能做出具有完整指令集的處理器 CPU0sc.v,以下是 處理器 CPU0sc.v 的完整 Verilog 原始碼。
檔案:cpu0sc.v
`define PC R[15] // 程式計數器
`define LR R[14] // 連結暫存器
`define SP R[13] // 堆疊暫存器
`define SW R[12] // 狀態暫存器
// 狀態暫存器旗標位元
`define N `SW[31] // 負號旗標
`define Z `SW[30] // 零旗標
`define C `SW[29] // 進位旗標
`define V `SW[28] // 溢位旗標
`define I `SW[7] // 硬體中斷許可
`define T `SW[6] // 軟體中斷許可
`define M `SW[0] // 模式位元
module cpu0c(input clock); // CPU0-Mini 的快取版:cpu0mc 模組
parameter [7:0] LD=8'h00,ST=8'h01,LDB=8'h02,STB=8'h03,LDR=8'h04,STR=8'h05,
LBR=8'h06,SBR=8'h07,ADDI=8'h08,CMP=8'h10,MOV=8'h12,ADD=8'h13,SUB=8'h14,
MUL=8'h15,DIV=8'h16,AND=8'h18,OR=8'h19,XOR=8'h1A,ROL=8'h1C,ROR=8'h1D,
SHL=8'h1E,SHR=8'h1F,JEQ=8'h20,JNE=8'h21,JLT=8'h22,JGT=8'h23,JLE=8'h24,
JGE=8'h25,JMP=8'h26,SWI=8'h2A,CALL=8'h2B,RET=8'h2C,IRET=8'h2D,
PUSH=8'h30,POP=8'h31,PUSHB=8'h32,POPB=8'h33;
reg signed [31:0] R [0:15]; // 宣告暫存器 R[0..15] 等 16 個 32 位元暫存器
reg signed [31:0] IR; // 指令暫存器 IR
reg [7:0] m [0:256]; // 內部的快取記憶體
reg [7:0] op; // 變數:運算代碼 op
reg [3:0] ra, rb, rc; // 變數:暫存器代號 ra, rb, rc
reg [4:0] c5; // 變數:5 位元常數 c5
reg signed [11:0] c12; // 變數:12 位元常數 c12
reg signed [15:0] c16; // 變數:16 位元常數 c16
reg signed [23:0] c24; // 變數:24 位元常數 c24
reg signed [31:0] sp, jaddr, laddr, raddr;
reg signed [31:0] temp;
reg signed [31:0] pc;
integer i;
initial // 初始化
begin
`PC = 0; // 將 PC 設為起動位址 0
`SW = 0;
R[0] = 0; // 將 R[0] 暫存器強制設定為 0
$readmemh("cpu0s.hex", m);
for (i=0; i < 255; i=i+4) begin
$display("%8x: %8x", i, {m[i], m[i+1], m[i+2], m[i+3]});
end
end
always @(posedge clock) begin // 在 clock 時脈的正邊緣時觸發
pc = `PC;
IR = {m[`PC], m[`PC+1], m[`PC+2], m[`PC+3]}; // 指令擷取階段:IR=m[PC], 4 個 Byte 的記憶體
`PC = `PC+4; // 擷取完成,PC 前進到下一個指令位址
{op,ra,rb,rc,c12} = IR; // 解碼階段:將 IR 解為 {op, ra, rb, rc, c12}
c5 = IR[4:0];
c24 = IR[23:0];
c16 = IR[15:0];
jaddr = `PC+c16;
laddr = R[rb]+c16;
raddr = R[rb]+R[rc];
case (op) // 根據 OP 執行對應的動作
LD: begin // 載入指令: R[ra] = m[addr]
R[ra] = {m[laddr], m[laddr+1], m[laddr+2], m[laddr+3]};
$display("%4dns %8x : LD R%-d R%-d 0x%x ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, c16, ra, R[ra], R[ra]);
end
ST: begin // 儲存指令: m[addr] = R[ra]
{m[laddr], m[laddr+1], m[laddr+2], m[laddr+3]} = R[ra];
$display("%4dns %8x : ST R%-d R%-d 0x%x ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, c16, ra, R[ra], R[ra]);
end
LDB:begin // 載入byte; LDB Ra, [Rb+ Cx]; Ra<=(byte)[Rb+ Cx]
R[ra] = { 24'b0, m[laddr] };
$display("%4dns %8x : LDB R%-d R%-d 0x%x ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, c16, ra, R[ra], R[ra]);
end
STB:begin // 儲存byte; STB Ra, [Rb+ Cx]; Ra=>(byte)[Rb+ Cx]
m[laddr] = R[ra][7:0];
$display("%4dns %8x : STB R%-d R%-d 0x%x ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, c16, ra, R[ra], R[ra]);
end
LDR:begin // LD 的 Rc 版; LDR Ra, [Rb+Rc]; Ra<=[Rb+ Rc]
R[ra] = {m[raddr], m[raddr+1], m[raddr+2], m[raddr+3]};
$display("%4dns %8x : LDR R%-d R%-d R%-d ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, rc, ra, R[ra], R[ra]);
end
STR:begin // ST 的 Rc 版; STR Ra, [Rb+Rc]; Ra=>[Rb+ Rc]
{m[raddr], m[raddr+1], m[raddr+2], m[raddr+3]} = R[ra];
$display("%4dns %8x : STR R%-d R%-d R%-d ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, rc, ra, R[ra], R[ra]);
end
LBR:begin // LDB 的 Rc 版; LBR Ra, [Rb+Rc]; Ra<=(byte)[Rb+ Rc]
R[ra] = { 24'b0, m[raddr] };
$display("%4dns %8x : LBR R%-d R%-d R%-d ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, rc, ra, R[ra], R[ra]);
end
SBR:begin // STB 的 Rc 版; SBR Ra, [Rb+Rc]; Ra=>(byte)[Rb+ Rc]
m[raddr] = R[ra][7:0];
$display("%4dns %8x : SBR R%-d R%-d R%-d ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, rc, ra, R[ra], R[ra]);
end
MOV:begin // 移動; MOV Ra, Rb; Ra<=Rb
R[ra] = R[rb];
$display("%4dns %8x : MOV R%-d R%-d ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, ra, R[ra], R[ra]);
end
CMP:begin // 比較; CMP Ra, Rb; SW=(Ra >=< Rb)
temp = R[ra]-R[rb];
`N=(temp<0);`Z=(temp==0);
$display("%4dns %8x : CMP R%-d R%-d ; SW=0x%x", $stime, pc, ra, rb, `SW);
end
ADDI:begin // R[a] = Rb+c16; // 立即值加法; LDI Ra, Rb+Cx; Ra<=Rb + Cx
R[ra] = R[rb]+c16;
$display("%4dns %8x : ADDI R%-d R%-d %-d ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, c16, ra, R[ra], R[ra]);
end
ADD: begin // 加法指令: R[ra] = R[rb]+R[rc]
R[ra] = R[rb]+R[rc];
$display("%4dns %8x : ADD R%-d R%-d R%-d ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, rc, ra, R[ra], R[ra]);
end
SUB:begin // 減法; SUB Ra, Rb, Rc; Ra<=Rb-Rc
R[ra] = R[rb]-R[rc];
$display("%4dns %8x : SUB R%-d R%-d R%-d ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, rc, ra, R[ra], R[ra]);
end
MUL:begin // 乘法; MUL Ra, Rb, Rc; Ra<=Rb*Rc
R[ra] = R[rb]*R[rc];
$display("%4dns %8x : MUL R%-d R%-d R%-d ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, rc, ra, R[ra], R[ra]);
end
DIV:begin // 除法; DIV Ra, Rb, Rc; Ra<=Rb/Rc
R[ra] = R[rb]/R[rc];
$display("%4dns %8x : DIV R%-d R%-d R%-d ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, rc, ra, R[ra], R[ra]);
end
AND:begin // 位元 AND; AND Ra, Rb, Rc; Ra<=Rb and Rc
R[ra] = R[rb]&R[rc];
$display("%4dns %8x : AND R%-d R%-d R%-d ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, rc, ra, R[ra], R[ra]);
end
OR:begin // 位元 OR; OR Ra, Rb, Rc; Ra<=Rb or Rc
R[ra] = R[rb]|R[rc];
$display("%4dns %8x : OR R%-d R%-d R%-d ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, rc, ra, R[ra], R[ra]);
end
XOR:begin // 位元 XOR; XOR Ra, Rb, Rc; Ra<=Rb xor Rc
R[ra] = R[rb]^R[rc];
$display("%4dns %8x : XOR R%-d R%-d R%-d ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, rc, ra, R[ra], R[ra]);
end
SHL:begin // 向左移位; SHL Ra, Rb, Cx; Ra<=Rb << Cx
R[ra] = R[rb]<<c5;
$display("%4dns %8x : SHL R%-d R%-d %-d ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, c5, ra, R[ra], R[ra]);
end
SHR:begin // 向右移位; SHR Ra, Rb, Cx; Ra<=Rb >> Cx
R[ra] = R[rb]>>c5;
$display("%4dns %8x : SHR R%-d R%-d %-d ; R%-2d=0x%8x=%-d", $stime, pc, ra, rb, c5, ra, R[ra], R[ra]);
end
JMP:begin // 跳躍指令: PC = PC + cx24
`PC = `PC + c24;
$display("%4dns %8x : JMP 0x%x ; PC=0x%x", $stime, pc, c24, `PC);
end
JEQ:begin // 跳躍 (相等); JEQ Cx; if SW(=) PC PC+Cx
if (`Z) `PC=`PC+c24;
$display("%4dns %8x : JEQ 0x%08x ; PC=0x%x", $stime, pc, c24, `PC);
end
JNE:begin // 跳躍 (不相等); JNE Cx; if SW(!=) PC PC+Cx
if (!`Z) `PC=`PC+c24;
$display("%4dns %8x : JNE 0x%08x ; PC=0x%x", $stime, pc, c24, `PC);
end
JLT:begin // 跳躍 ( < ); JLT Cx; if SW(<) PC PC+Cx
if (`N) `PC=`PC+c24;
$display("%4dns %8x : JLT 0x%08x ; PC=0x%x", $stime, pc, c24, `PC);
end
JGT:begin // 跳躍 ( > ); JGT Cx; if SW(>) PC PC+Cx
if (!`N&&!`Z) `PC=`PC+c24;
$display("%4dns %8x : JGT 0x%08x ; PC=0x%x", $stime, pc, c24, `PC);
end
JLE:begin // 跳躍 ( <= ); JLE Cx; if SW(<=) PC PC+Cx
if (`N || `Z) `PC=`PC+c24;
$display("%4dns %8x : JLE 0x%08x ; PC=0x%x", $stime, pc, c24, `PC);
end
JGE:begin // 跳躍 ( >= ); JGE Cx; if SW(>=) PC PC+Cx
if (!`N || `Z) `PC=`PC+c24;
$display("%4dns %8x : JGE 0x%08x ; PC=0x%x", $stime, pc, c24, `PC);
end
SWI:begin // 軟中斷; SWI Cx; LR <= PC; PC <= Cx; INT<=1
`LR=`PC;`PC= c24; `I = 1'b1;
$display("%4dns %8x : SWI 0x%08x ; PC=0x%x", $stime, pc, c24, `PC);
end
CALL:begin // 跳到副程式; CALL Cx; LR<=PC; PC<=PC+Cx
`LR=`PC;`PC=`PC + c24;
$display("%4dns %8x : CALL 0x%08x ; PC=0x%x", $stime, pc, c24, `PC);
end
RET:begin // 返回; RET; PC <= LR
`PC=`LR;
$display("%4dns %8x : RET ; PC=0x%x", $stime, pc, `PC);
if (`PC<0) $finish;
end
IRET:begin // 中斷返回; IRET; PC <= LR; INT<=0
`PC=`LR;`I = 1'b0;
$display("%4dns %8x : IRET ; PC=0x%x", $stime, pc, `PC);
end
PUSH:begin // 推入 word; PUSH Ra; SP-=4;[SP]<=Ra;
sp = `SP-4; `SP = sp; {m[sp], m[sp+1], m[sp+2], m[sp+3]} = R[ra];
$display("%4dns %8x : PUSH R%-d ; R%-2d=0x%8x, SP=0x%x", $stime, pc, ra, ra, R[ra], `SP);
end
POP:begin // 彈出 word; POP Ra; Ra=[SP];SP+=4;
sp = `SP; R[ra]={m[sp], m[sp+1], m[sp+2], m[sp+3]}; `SP = sp+4;
$display("%4dns %8x : POP R%-d ; R%-2d=0x%8x, SP=0x%x", $stime, pc, ra, ra, R[ra], `SP);
end
PUSHB:begin // 推入 byte; PUSHB Ra; SP--;[SP]<=Ra;(byte)
sp = `SP-1; `SP = sp; m[sp] = R[ra];
$display("%4dns %8x : PUSHB R%-d ; R[%-d]=0x%8x, SP=0x%x", $stime, pc, ra, ra, R[ra], `SP);
end
POPB:begin // 彈出 byte; POPB Ra; Ra<=[SP];SP++;(byte)
sp = `SP+1; `SP = sp; R[ra]=m[sp];
$display("%4dns %8x : POPB R%-d ; R[%-d]=0x%8x, SP=0x%x", $stime, pc, ra, ra, R[ra], `SP);
end
endcase
end
endmodule
module main; // 測試程式開始
reg clock; // 時脈 clock 變數
cpu0c cpu(clock); // 宣告 cpu0mc 處理器
initial clock = 0; // 一開始 clock 設定為 0
always #10 clock=~clock; // 每隔 10 奈秒將 clock 反相,產生週期為 20 奈秒的時脈
initial #2000 $finish; // 在 640 奈秒的時候停止測試。(因為這時的 R[1] 恰好是 1+2+...+10=55 的結果)
endmodule程式碼解析與執行
在上一期的 CPU0mc.v 當中,我們直接使用下列程式將「機器碼」塞入到記憶體當中,但是這樣做顯然彈性不太夠。
{m[0],m[1],m[2],m[3]} = 32'h001F0018; // 0000 LD R1, K1
{m[4],m[5],m[6],m[7]} = 32'h002F0010; // 0004 LD R2, K0
{m[8],m[9],m[10],m[11]} = 32'h003F0014; // 0008 LD R3, SUM
{m[12],m[13],m[14],m[15]}= 32'h13221000; // 000C LOOP: ADD R2, R2, R1
{m[16],m[17],m[18],m[19]}= 32'h13332000; // 0010 ADD R3, R3, R2
{m[20],m[21],m[22],m[23]}= 32'h26FFFFF4; // 0014 JMP LOOP
{m[24],m[25],m[26],m[27]}= 32'h00000000; // 0018 K0: WORD 0
{m[28],m[29],m[30],m[31]}= 32'h00000001; // 001C K1: WORD 1
{m[32],m[33],m[34],m[35]}= 32'h00000000; // 0020 SUM: WORD 0因此,在本期的 CPU0sc.v 這個程式中,我們採用讀取外部檔案的方式,將機器碼寫在 「cpu0s.hex」這個檔案中, 然後再用下列指令將該 16 進位的機器碼檔案讀入。
$readmemh("cpu0s.hex", m);其中的 readmemh 是一個可以讀取 16 進位的文字檔的函數,上述指令會將 cpu0s.hex 這個檔案內的 16 進位字串 讀入到「記憶體變數」 m 當中。
以下是 cpu0s.hex 的完整內容。
輸入檔:cpu0s.hex
00 DF 00 B6 // 0 LD R13, StackEnd
08 40 00 04 // 4 ADDI R4, 4
08 50 00 08 // 8 ADDI R5, 8
05 4D 50 00 // c STR R4, [R13+R5]
04 6D 50 00 // 10 LDR R6, [R13+R5]
07 5D 40 00 // 14 SBR R5, [R13+R4]
06 6D 40 00 // 18 LBR R6, [R13+R4]
08 E0 FF FF // 1C ADDI R14,R0,-1
30 E0 00 00 // 20 PUSH R14
13 85 40 00 // 24 ADD R8, R5, R4
14 85 40 00 // 28 SUB R8, R5, R4
15 85 40 00 // 2c MUL R8, R5, R4
16 85 40 00 // 30 DIV R8, R5, R4
18 85 40 00 // 34 AND R8, R5, R4
19 85 40 00 // 38 OR R8, R5, R4
1A 85 40 00 // 3c XOR R8, R5, R4
1E 85 00 03 // 40 SHL R8, R5, 3
1F 85 00 02 // 44 SHR R8, R5, 2
10 45 00 00 // 48 CMP R4, R5
20 00 00 18 // 4c JEQ L1
23 00 00 14 // 50 JGT L1
25 00 00 10 // 54 JGE L1
22 00 00 0C // 58 JLT L1
24 00 00 08 // 5c JLE L1
21 00 00 04 // 60 JNE L1
26 00 00 00 // 64 JMP L1
08 10 00 0A // 68 L1: ADDI R1, R0, 10
2B 00 00 08 // 6c CALL SUM
31 E0 00 00 // 70 POP R14
2C 00 00 00 // 74 RET
30 E0 00 00 // 78 SUM: PUSH R14
12 30 00 00 // 7c MOV R3, R0 // R3 = i = 0
02 4F 00 24 // 80 LDB R4, k1 // R4 = 1
08 20 00 00 // 84 ADDI R2, 0 // SUM = R2 = 0
13 22 30 00 // 88 LOOP: ADD R2, R2, R3 // SUM = SUM + i
13 33 40 00 // 8c ADD R3, R3, R4 // i = i + 1
10 31 00 00 // 90 CMP R3, R1 // if (i < R1)
24 FF FF F0 // 94 JLE LOOP // goto LOOP
01 2F 00 0D // 98 ST R2, s
03 3F 00 0D // 9c STB R3, i
31 E0 00 00 // a0 POP R14
2C 00 00 00 // a4 RET // return
01 // a8 k1: BYTE 1 // char K1=1
00 00 00 00 // a9 s: WORD 0 // int s
00 // ad i: BYTE 0 // char i=1
00 01 02 03 // ae Stack: BYTE 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 , 10, 11
04 05 06 07 // b2
08 09 0A 0B // b6
00 00 00 BA // ba StackEnd: WORD StackEnd
01 02 03 04 // be Data: BYTE 0, 1, 2, 3, 4, 5, 6, 7, 8
05 06 07 08 // c2上述程式的內容,大致是先準備好堆疊,然後就開始測試 ADDI, STR, LDR, ADD, SUB, ... 等指令。 接著在呼叫 CMP R4, R5 之後進行跳躍測試動作,由於 R4=4, R5=8,所以 CMP 的結果會是「小於」, 因此在後面的 JEQ, JGT, JGE 等指令都不會真的跳躍,直到執行 JLT L1 時就會真的跳到 L1 去。
接著用 ADDI R1, R0, 10 將 R1 設為 10,然後就用 CALL SUM 這個指令呼叫 SUM 這個副程式,於是跳到 位於 0x78 的 SUM: PUSH R14 這一行,並開始執行副程式,該副程式會計算 1+2+...+R1 的結果,放在 R2 當中, 並在最後用 STB R2, s 這個指令存入變數 s 當中,然後在執行完 RET 指令後返回上一層,也就是 0x70 行的 POP R14 指令,接著在執行 RET 指令時,由於此時 R14 為 -1,因此 Verilog 程式就在完成 RET 指令時發現 PC 已經小於 0 了,因此執行$finish` 指令停止整個程式。
RET:begin // 返回; RET; PC <= LR
`PC=`LR;
$display("%4dns %8x : RET ; PC=0x%x", $stime, pc, `PC);
if (`PC<0) $finish;
end執行結果
有了上述的程式 cpu0sc.v 與輸入的機器碼 cpu0s.hex 檔案之後,我們就可以用下列指令進行編譯與執行, 以下是該程式編譯與執行的結果。
D:\verilog>iverilog -o cpu0sc cpu0sc.v
D:\verilog>vvp cpu0sc
WARNING: cpu0sc.v:40: $readmemh(cpu0s.hex): Not enough words in the file for the
requested range [0:256].
00000000: 00df00b6
00000004: 08400004
00000008: 08500008
0000000c: 054d5000
00000010: 046d5000
00000014: 075d4000
00000018: 066d4000
0000001c: 08e0ffff
00000020: 30e00000
00000024: 13854000
00000028: 14854000
0000002c: 15854000
00000030: 16854000
00000034: 18854000
00000038: 19854000
0000003c: 1a854000
00000040: 1e850003
00000044: 1f850002
00000048: 10450000
0000004c: 20000018
00000050: 23000014
00000054: 25000010
00000058: 2200000c
0000005c: 24000008
00000060: 21000004
00000064: 26000000
00000068: 0810000a
0000006c: 2b000008
00000070: 31e00000
00000074: 2c000000
00000078: 30e00000
0000007c: 12300000
00000080: 024f0024
00000084: 08200000
00000088: 13223000
0000008c: 13334000
00000090: 10310000
00000094: 24fffff0
00000098: 012f000d
0000009c: 033f000d
000000a0: 31e00000
000000a4: 2c000000
000000a8: 01000000
000000ac: 00000001
000000b0: 02030405
000000b4: 06070809
000000b8: 0a0b0000
000000bc: 00ba0102
000000c0: 03040506
000000c4: 0708xxxx
000000c8: xxxxxxxx
000000cc: xxxxxxxx
000000d0: xxxxxxxx
000000d4: xxxxxxxx
000000d8: xxxxxxxx
000000dc: xxxxxxxx
000000e0: xxxxxxxx
000000e4: xxxxxxxx
000000e8: xxxxxxxx
000000ec: xxxxxxxx
000000f0: xxxxxxxx
000000f4: xxxxxxxx
000000f8: xxxxxxxx
000000fc: xxxxxxxx
10ns 00000000 : LD R13 R15 0x00b6 ; R13=0x000000ba=186
30ns 00000004 : ADDI R4 R0 4 ; R4 =0x00000004=4
50ns 00000008 : ADDI R5 R0 8 ; R5 =0x00000008=8
70ns 0000000c : STR R4 R13 R5 ; R4 =0x00000004=4
90ns 00000010 : LDR R6 R13 R5 ; R6 =0x00000004=4
110ns 00000014 : SBR R5 R13 R4 ; R5 =0x00000008=8
130ns 00000018 : LBR R6 R13 R4 ; R6 =0x00000008=8
150ns 0000001c : ADDI R14 R0 -1 ; R14=0xffffffff=-1
170ns 00000020 : PUSH R14 ; R14=0xffffffff, SP=0x000000b6
190ns 00000024 : ADD R8 R5 R4 ; R8 =0x0000000c=12
210ns 00000028 : SUB R8 R5 R4 ; R8 =0x00000004=4
230ns 0000002c : MUL R8 R5 R4 ; R8 =0x00000020=32
250ns 00000030 : DIV R8 R5 R4 ; R8 =0x00000002=2
270ns 00000034 : AND R8 R5 R4 ; R8 =0x00000000=0
290ns 00000038 : OR R8 R5 R4 ; R8 =0x0000000c=12
310ns 0000003c : XOR R8 R5 R4 ; R8 =0x0000000c=12
330ns 00000040 : SHL R8 R5 3 ; R8 =0x00000040=64
350ns 00000044 : SHR R8 R5 2 ; R8 =0x00000002=2
370ns 00000048 : CMP R4 R5 ; SW=0x80000000
390ns 0000004c : JEQ 0x00000018 ; PC=0x00000050
410ns 00000050 : JGT 0x00000014 ; PC=0x00000054
430ns 00000054 : JGE 0x00000010 ; PC=0x00000058
450ns 00000058 : JLT 0x0000000c ; PC=0x00000068
470ns 00000068 : ADDI R1 R0 10 ; R1 =0x0000000a=10
490ns 0000006c : CALL 0x00000008 ; PC=0x00000078
510ns 00000078 : PUSH R14 ; R14=0x00000070, SP=0x000000b2
530ns 0000007c : MOV R3 R0 ; R3 =0x00000000=0
550ns 00000080 : LDB R4 R15 0x0024 ; R4 =0x00000001=1
570ns 00000084 : ADDI R2 R0 0 ; R2 =0x00000000=0
590ns 00000088 : ADD R2 R2 R3 ; R2 =0x00000000=0
610ns 0000008c : ADD R3 R3 R4 ; R3 =0x00000001=1
630ns 00000090 : CMP R3 R1 ; SW=0x80000000
650ns 00000094 : JLE 0x00fffff0 ; PC=0x00000088
670ns 00000088 : ADD R2 R2 R3 ; R2 =0x00000001=1
690ns 0000008c : ADD R3 R3 R4 ; R3 =0x00000002=2
710ns 00000090 : CMP R3 R1 ; SW=0x80000000
730ns 00000094 : JLE 0x00fffff0 ; PC=0x00000088
750ns 00000088 : ADD R2 R2 R3 ; R2 =0x00000003=3
770ns 0000008c : ADD R3 R3 R4 ; R3 =0x00000003=3
790ns 00000090 : CMP R3 R1 ; SW=0x80000000
810ns 00000094 : JLE 0x00fffff0 ; PC=0x00000088
830ns 00000088 : ADD R2 R2 R3 ; R2 =0x00000006=6
850ns 0000008c : ADD R3 R3 R4 ; R3 =0x00000004=4
870ns 00000090 : CMP R3 R1 ; SW=0x80000000
890ns 00000094 : JLE 0x00fffff0 ; PC=0x00000088
910ns 00000088 : ADD R2 R2 R3 ; R2 =0x0000000a=10
930ns 0000008c : ADD R3 R3 R4 ; R3 =0x00000005=5
950ns 00000090 : CMP R3 R1 ; SW=0x80000000
970ns 00000094 : JLE 0x00fffff0 ; PC=0x00000088
990ns 00000088 : ADD R2 R2 R3 ; R2 =0x0000000f=15
1010ns 0000008c : ADD R3 R3 R4 ; R3 =0x00000006=6
1030ns 00000090 : CMP R3 R1 ; SW=0x80000000
1050ns 00000094 : JLE 0x00fffff0 ; PC=0x00000088
1070ns 00000088 : ADD R2 R2 R3 ; R2 =0x00000015=21
1090ns 0000008c : ADD R3 R3 R4 ; R3 =0x00000007=7
1110ns 00000090 : CMP R3 R1 ; SW=0x80000000
1130ns 00000094 : JLE 0x00fffff0 ; PC=0x00000088
1150ns 00000088 : ADD R2 R2 R3 ; R2 =0x0000001c=28
1170ns 0000008c : ADD R3 R3 R4 ; R3 =0x00000008=8
1190ns 00000090 : CMP R3 R1 ; SW=0x80000000
1210ns 00000094 : JLE 0x00fffff0 ; PC=0x00000088
1230ns 00000088 : ADD R2 R2 R3 ; R2 =0x00000024=36
1250ns 0000008c : ADD R3 R3 R4 ; R3 =0x00000009=9
1270ns 00000090 : CMP R3 R1 ; SW=0x80000000
1290ns 00000094 : JLE 0x00fffff0 ; PC=0x00000088
1310ns 00000088 : ADD R2 R2 R3 ; R2 =0x0000002d=45
1330ns 0000008c : ADD R3 R3 R4 ; R3 =0x0000000a=10
1350ns 00000090 : CMP R3 R1 ; SW=0x40000000
1370ns 00000094 : JLE 0x00fffff0 ; PC=0x00000088
1390ns 00000088 : ADD R2 R2 R3 ; R2 =0x00000037=55
1410ns 0000008c : ADD R3 R3 R4 ; R3 =0x0000000b=11
1430ns 00000090 : CMP R3 R1 ; SW=0x00000000
1450ns 00000094 : JLE 0x00fffff0 ; PC=0x00000098
1470ns 00000098 : ST R2 R15 0x000d ; R2 =0x00000037=55
1490ns 0000009c : STB R3 R15 0x000d ; R3 =0x0000000b=11
1510ns 000000a0 : POP R14 ; R14=0x00000070, SP=0x000000b6
1530ns 000000a4 : RET ; PC=0x00000070
1550ns 00000070 : POP R14 ; R14=0xffffffff, SP=0x000000ba
1570ns 00000074 : RET ; PC=0xffffffff結語
從這兩期的程式中,您應該可以瞭解到直接使用高階的 Verilog 流程式語法來設計處理器,像是 cpu0mc.v 與 cpu0sc.v , 都是相當容易的事,這完全是因為 verilog 支援了相當高階的運算,像是 「+, -, *, /, &, |, ^, <<, >>」等運算的原故。
不過、在上述程式當中,我們並沒有支援「硬體中斷」的功能,也沒有實作「軟體中斷」SWI 的函數呼叫,這樣 CPU0sc.v 就 只能是一顆單工 (Single Task) 的處理器,而無法支援多工 (Multi Task) 的功能了。
在下期中,我們將繼續擴充 CPU0sc.v 這個程式,加入支援「軟硬體中斷」的功能,該程式稱為 CPU0ic.v (i 代表 Interrupt, c 代表 cache memory)。
然後我們將再度用 16 進位的方式,寫出一個機器語言的程式,可以同時執行兩個「行程」(Task) ,並且每隔一小段時間就利用 硬體中斷進行「行程切換」,以示範如何設計一個可以支援「多工」能力的 CPU 處理器。
參考文獻
R 講題分享 – SpideR -- 用R自製網路爬蟲收集資料 (作者:Taiwan R User Group)
大家好,這篇文章是取材自EC於10月份在Taiwan R User Group的分享內容。他從社群過去分享的內容中學習,撰寫了一個網路爬蟲來收集中國的新聞。以下是他的心得分享。
工具
EC主要是利用以下的R套件來達成任務:
Rcurl
Rcurl是提供R使用網際網路上各種通訊協定的工具。EC主要是透過Rcurl來製作Query的格式來自動化下載網站內容的動作。
XML
下載後的內容是HTML格式,無法直接分析。所以EC再利用XML套件的readHTMLTable和XPath的功能來將需要的資訊從文件中萃取出來。
RMessenger(監控用, powered by Wush)
由於要爬的資料很大,EC需要使用很多機器跑數天的程式。又因為網路環境很容易出錯,EC需要有工具在出錯的時候通知他。RMessenger是提供R傳送即時訊息的功能,讓EC能在第一時間得知出錯的狀況。
結果
最後EC總共發出了1,538,992 個Queries和抓取了25,828,673 篇文章。
注意事項
以下的兩大原則可以讓大家避免潛在的麻煩。
版權所有原則
抓取資料前,應先檢視網站對於抓取與運用資料的宣告。即便網站中沒有明確的版權聲明、資料可公開為所有人自由擷取且現行法規對於電子著作權的保護仍模糊的情境下,但我方在應用抓下的資料時,仍應假定該網站擁有所有的版權(All Rights Reserved)。
盡量匿蹤原則
爬蟲程式可以說是駭客行為(Hacking)的一種,我們可以將它定義為「採取跳脫常規的作法,以有創意的方式抓取網頁資料的程序」。由定義可知,爬蟲程式是一種正面的作為,但由於它通常會耗用掉網站的大量資源(網路法律界引入了「侵入動產(trespass to chattels)」的概念,其意指他人阻止或損害擁有者使用其財產的權益。),因此爬蟲程式並不為網站擁有者所樂見。對此,我方應儘量善待對方的網路資源,且盡可能偽裝成一般使用者,以免帶來不必要的法律困擾且讓爬蟲程式可以長久運作。以下是一些相關的心得:
- 儘量第一次發Query就做對,不要有太多異常的Query。
- 尊重和珍惜網路流量資源。不要吃光對方的流量,也不要干擾到對方的正常服務。
- 可以用Proxy服務作跳板,如TOR,但是請小心謹慎的使用,珍惜公共資源。
- 儘量在使用者多得時候混在使用者中,避免在離峰時間出沒以免被注意。
- 發Query的行為儘量偽裝成正常使用者,如:
- 每抓取一筆資料後,隨機等待一段時間後再行動(使用 sleep + rand 函數)。
- 每天自不同的時間開始行動,亦即系統排程不要太有規律。
- 限制每天抓取的總流量,這樣才能細水長流。
抓取網頁資料的標準作業程序
分析網頁的表單(Form)格式(逆向工程),以製定Query格式
分析表單的細節解說請參考c3h3於TW use-R在20130818 MLDM spideR的演講。在此演講中,EC分享了兩個工具來分析網頁:
處理抓下來的資料
由於不熟悉Encoding的知識,開發者常常需要花費大量的時間在處理Encoding的問題。尤其處理到中文資料時,不同作業系統預設的Encoding也不相同,往往讓開發者看到亂碼而八丈摸不著頭緒,以為是資料抓錯了。EC介紹了一些關於Encoding的知識:
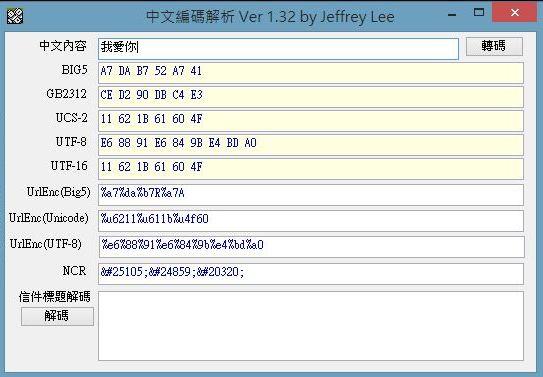
什麼是Charcter Encoding/字元編碼/字符編碼
文字資料儲存到電腦後,最終都是0和1的位元序列。Encoding則是電腦用來把位元序列轉譯成人類看得懂的文字的格式。例如下圖就表示數種不同Encoding表示「我愛你」的位元序列格式:
ps. 一般表示序列的時候,會使用16進位的符號來簡化表示位元序列。如: - 1 代表 0001 - 8 代表 1000 - F 代表 1111
所以如果Encoding的設定不正確,電腦就沒辦法把資料正確的轉換成文字供人類閱讀。
作業系統使用的繁體中文Encoding
當我們在處理中文資料時,很不幸的,不同作業系統預設的中文編碼是不同的。
Windows系統預設是Big5,Linux系統預設則是UTF-8,所以如果在Linux上處理Windows中撰寫的中文檔案,很大的機會會看到亂碼。
R IDE的Encoding
除了作業系統預設的編碼不同外,R IDE的預設編碼在不同的作業系統下亦有不同的編碼方式,這可能是源自於預設安裝的設定不同,也可能因為使用者安裝後自行做了修改。以RStudio為例,其在Windows/Mac/Linux等作業系統下的編碼方式可能不同的設定(使用者可以透過Menu->Tools->Global Options->General->Default text encoding查看),稍後會介紹Sys.getlocale()或sessionInfo()函數查詢Ecoding的設定。
讀取檔案或網頁的Encoding
若開啟的檔案或下載的網頁有亂碼的問題,通常係發送端與接收端的Encoding設定不同所致。亂碼除了極難閱讀外,更甚者,會使程式因為讀到特殊字元而致使載入資料不完全或異常中斷,這些錯誤都不易除錯。對此,有國外的技術論壇建議以「UTF-8(檔首無BOM)」進行編碼比較能避免錯誤發生。
R 如何處理Encoding
以下精要彙整此次開發spideR中,使用到與Encoding有關的R 相關函數:
- 查詢現行環境下的Encoding設定
- Sys.getlocale()
- sessionInfo()
- 修改現行環境下的Encoding設定
Sys.setlocale() :例如:Sys.setlocale(category='LC_ALL', locale='C')
- 以特定Encoding載入文字檔
- read.table() :例如:myStrVec <- read.table(myFile, ... , encoding='UTF-8')
- 載入特定檔後轉換Encoding
- Encoding() :例如:Encoding(myStrVec) <- 'gb2312'
- iconv() :例如:myURL <- iconv(myStrVec[i], from='UTF-8', to='gb2312')
- 送出Query URL的Encoding
- URLencode() :例如:myURL <- URLencode(myURL)
- 接收Query結果的Encoding
- getURL() :例如:myRes <- getURL(myURL, ... , .encoding='gb2312')
- readLines() :例如:myRes <- readLines(myURL, encoding='gb2312')
readHTMLTable() :例如:myRes <- readHTMLTable(myRes, encoding='gb2312', which= ...)
當R IDE 開發spideR 面對Encoding 的解決方案
EC寫這支spideR程式共花了七天,但卻有五天是在嘗試解決上述Encoding所導致的問題。經過了幾經的嘗試與搜尋國外的技術論壇(特別推薦Stack Overflow )後,建議一個可以避免Encoding的解決方案供大家參考。
- 程式開始處,先將Encoding 轉成選項'C'
- Sys.setlocale(category='LC_ALL', locale='C')
- 中間依據需求統一轉成特定編碼
- myStrVec = read.table('myFile.csv', sep=',', ... , encoding='UTF-8')
- myStr <- iconv(myStrVec[i], from='UTF-8', to='gb2312')
- myURL <- URLencode(myStr)
- myRes <- getURL(myURL, ... , .encoding='gb2312')
- myRes <- readHTMLTable(myRes, encoding='gb2312', which= ...)
- 程式結尾處再轉回原Encoding 設定,選項為''(此步驟可略)
- Sys.setlocale(category='LC_ALL', locale='')
參考資料
- Taiwan R User Group
- 20130818 MLDM spideR (Ronny Wang)
- 20130325 MLDM spideR -1 (c3h3)
- 20130325 MLDM spideR -2 (c3h3)
- Schrenk, M. (2012), Webbots, Spiders, and Screen Scrapers: A Guide to Developing Internet Agents with PHP/CURL, 2nd Edition, No Starch Press.
- COS 統計之都的RCurl引介
- Stack Overflow (很好的技術論壇)
- inside-R (比較美觀的 R 文件)
- 維基百科
- 网页爬虫-R语言实现,函数库文件 (DataGuru 煉數成金 )
- 矛與盾大對決 (PHP Conf. Taiwan 2013)
- 金融業菜鳥實習生的 Python Project 初體驗
作者
Wush Wu ()
- Taiwan R User Group Organizer
- R 相關著作:
- 研究領域:Large Scale Learning,Text Mining和Uncertain Time Series
Yi-Hsi (EC) Lee ()
- 中山大學財務管理博士(2003-2010)
- 中南大學管理與科學博士候選人(2009-迄今)
- 志方財務顧問有限公司總經理
- R 相關著作:
- spideR-中國新聞網
- spideR-eBay
- 研究領域:金融風險管理模型與系統開發、投資決策支援系統開發
雜誌訊息
讀者訂閱
程式人雜誌是一個結合「開放原始碼與公益捐款活動」的雜誌,簡稱「開放公益雜誌」。開放公益雜誌本著「讀書做善事、寫書做公益」的精神,我們非常歡迎程式人認養專欄、或者捐出您的網誌,如果您願意成為本雜誌的專欄作家,請加入 程式人雜誌社團 一同共襄盛舉。
我們透過發行這本雜誌,希望讓大家可以讀到想讀的書,學到想學的技術,同時也讓寫作的朋友的作品能產生良好價值 – 那就是讓讀者根據雜誌的價值捐款給慈善團體。 讀雜誌做公益也不需要有壓力,您不需要每讀一本就急著去捐款,您可以讀了十本再捐,或者使用固定的月捐款方式,當成是雜誌訂閱費,或者是季捐款、一年捐一次等都 OK ! 甚至是單純當個讀者我們也都很歡迎!
本雜誌每期參考價:NT 50 元,如果您喜歡本雜誌,請將書款捐贈公益團體。例如可捐贈給「羅慧夫顱顏基金會 彰化銀行(009) 帳號:5234-01-41778-800」。(若匯款要加註可用「程式人雜誌」五個字)
投稿須知
給專欄寫作者: 做公益不需要有壓力。如果您願意撰寫專欄,您可以輕鬆的寫,如果當月的稿件出不來,我們會安排其他稿件上場。
給網誌捐贈者: 如果您沒時間寫專欄或投稿,沒關係,只要將您的網誌以 [創作共用的「姓名標示、非商業性、相同方式分享」授權] 並通知我們,我們會自動從中選取需要的文章進行編輯,放入適當的雜誌當中出刊。
給文章投稿者: 程式人雜誌非常歡迎您加入作者的行列,如果您想撰寫任何文章或投稿,請用 markdown 或 LibreOffice 編輯好您的稿件,並於每個月 25 日前投稿到程式人雜誌社團 的檔案區,我們會盡可能將稿件編入隔月1號出版程式人雜誌當中,也歡迎您到社團中與我們一同討論。
如果您要投稿給程式人雜誌,我們最希望的格式是採用 markdown 的格式撰寫,然後將所有檔按壓縮為 zip 上傳到社團檔案區給我們, 如您想學習 markdown 的撰寫出版方式,可以參考 看影片學 markdown 編輯出版流程 一文。
如果您無法採用 markdown 的方式撰寫,也可以直接給我們您的稿件,像是 MS. Word 的 doc 檔或 LibreOffice 的 odt 檔都可以,我們 會將這些稿件改寫為 markdown 之後編入雜誌當中。
參與編輯
您也可以擔任程式人雜誌的編輯,甚至創造一個全新的公益雜誌,我們誠摯的邀請您加入「開放公益出版」的行列,如果您想擔任編輯或創造新雜誌,也歡迎到 程式人雜誌社團 來與我們討論相關事宜。
公益資訊
| 公益團體 | 聯絡資訊 | 服務對象 | 捐款帳號 |
|---|---|---|---|
| 財團法人羅慧夫顱顏基金會 | http://www.nncf.org/ 02-27190408分機 232 |
顱顏患者 (如唇顎裂、小耳症或其他罕見顱顏缺陷) | 銀行:009彰化銀行民生分行 帳號:5234-01-41778-800 |
| 社團法人台灣省兒童少年成長協會 | http://www.cyga.org/ 04-23058005 |
單親、隔代教養.弱勢及一般家庭之兒童青少年 | 銀行:新光銀行 戶名:台灣省兒童少年成長協會 帳號:103-0912-10-000212-0 |