程式人雜誌 -- 2014 年 1 月號 (開放公益出版品)

金融短訊：比特幣 (Bit Coin) 的運作原理

前言

最近比特幣漲到 900 美元，引起了很多注目，可惜我還不知道比特幣到底是甚麼碗糕？所以、想說趁編雜誌的機會 瞭解一下，比特幣到底是怎麼運作的。

2008 年日本的「中本聰」（Satoshi Nakamoto，化名）提出了一種數位貨幣，有興趣者請參考「中本聰」的原始論文：

隨後，他以開放、對等、共識、直接參與的理念為基準， 結合開源軟體和密碼學中塊密碼的工作模式，在P2P對等網路和分布式資料庫的平台上，開發出比特幣發行、 交易和帳戶管理的作業系統。其系統讓遍布整個對等網路使用者端的各節點，按照其種子檔案達成網路協定， 從而確保在貨幣發行、管理、流通等環節中公平、安全、可靠。並承諾比特幣將成為類似電子郵件的「電子現金」。實作在不需要審批、人人都有權發行的前提下，避免通貨膨脹，並無法偽造；支付完成之後，使用者就失去對該比特幣的所有權。2009年1月3日50個比特幣問世。

與傳統貨幣不同，比特幣執行機制不依賴中央銀行、政府、企業的支援或者信用擔保，而是依賴對等網路中種子檔案達成的網路協定，去中心化、自我完善的貨幣體制，理論上確保了任何人、機構、或政府都不可能操控比特幣的貨幣總量，或者製造通貨膨脹。它的貨幣總量按照設計預定的速率逐步增加，增加速度逐步放緩，並最終在2140年達到2100萬個的極限。

有多種途徑使用比特幣，透過電子貨幣交易所、服務商和個人等渠道，就能兌換為當地的現金或金幣；也可以直接使用它購買物品和服務。隨著接受比特幣支付的個人、組織、商家和企業的迅速增長，其匯率在四年內上漲了數千倍。 截止到2013年3月30日，全部發行比特幣按市價換算為美元後，總值突破為10億美元。雖然比特幣是目前使用最為廣泛的一種電子貨幣，但是除部分國家對虛擬貨幣有明文規定外，還沒有任何國家對比特幣的發行作出法律的規範和保障。

2009年1月3日，中本聰開創了比特幣P2P開源使用者群節點和雜湊函式系統，從此，其對等網路和它的第一個區塊鏈開始執行， 他發行了有史以來的第一組50個比特幣。

一年後，在比特幣論壇上，使用者群的自發交易中，產生了第一個比特幣公允匯率。該交易是一名使用者發送一萬個比特幣， 購買了一個披薩餅。目前，比特幣最為主要的參考匯率是 MT.GOX 交易所內比特幣與美元的成交匯率。

2013 年 11 月 18 日，在東京的 MT.GOX 市場交易的比特幣對美元匯率飆升至一對九百美元。

如果一塊披薩以 10 元美金計算的話，比特幣從 2010 年到 2013 年間，已經從萬分之十美元，漲到了九百美元，總共漲了 九十萬倍，這真是超級誇張的一種漲法啊！

比特幣的運作方法

比特幣是類似電子郵件的電子現金，交易雙方需要類似電子信箱的「比特幣錢包」和類似電郵位址的「比特幣位址」。和收發電子郵件一樣，匯款方透過電腦或智慧型手機，按收款方位址將比特幣直接付給對方。下列表格，列出了免費下載比特幣錢包和位址的部分網站。

使用者端名稱 網址 許可協定
Multibit（雲端資料區塊功能） http://multibit.org/ MIT
Bitcoin-Qt（中本聰使用者端） http://sourceforge.net/projects/bitcoin/ MIT
My Wallet（線上錢包，獨立式） https://blockchain.info/wallet 專有軟體
Coinbase（線上錢包，混合式） http://coinbase.com 專有軟體
Electrum http://electrum.ecdsa.org/ GPL
Armory（具有離線儲存功能） http://bitcoinarmory.com AGPL

舉例而言，「1DwunA9otZZQyhkVvkLJ8DV1tuSwMF7r3v」就是一個比特幣位址，比特幣位址是由 27 到 34 個之間的英文或數字所構成的，第一個字元只能是 1 或 3。(這個位址類似 RSA 當中的公鑰)

比特幣位址和私鑰是成對出現的，他們的關聯就像銀行卡號和密碼。比特幣位址就像銀行卡號一樣用來記錄你在該位址上存有多少比特幣。你可以隨意的生成比特幣位址來存放比特幣。每個比特幣位址在生成時，都會有一個相對應的該位址的私鑰被生成出來。這個私鑰可以證明你對該位址上的比特幣具有所有權。我們可以簡單的把比特幣位址理解成為銀行卡號，該位址的私鑰理解成為所對應銀行卡號的密碼。只有你在知道銀行密碼的情況下才能使用銀行卡號上的錢。所以，在使用比特幣錢包時請保存好你的位址和私鑰。

中本聰的論文

如果您瞭解 RSA 這樣的非對稱式金鑰加密系統，要瞭解比特幣的技術應該就不太難了。

透過公開金鑰的方式，我們可以設計出如下圖的加解密貨幣系統，來紀錄每一筆交易，但是這樣的系統有個弱點，就是沒辦法 防止同一塊錢 (coin) 被重複使用。

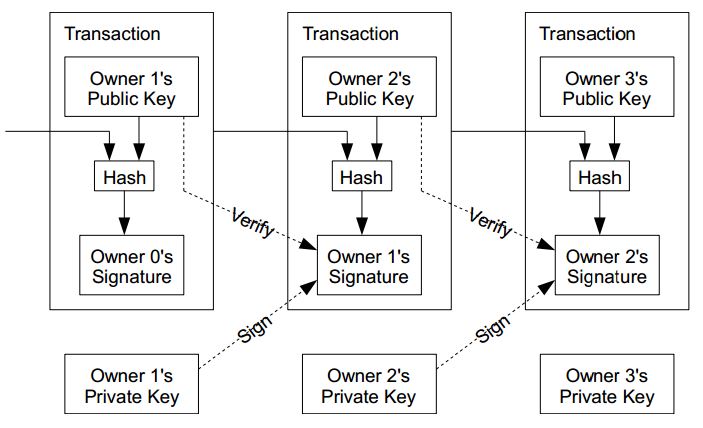
圖 1、傳統的數位貨幣系統架構圖

圖 1、傳統的數位貨幣系統架構圖

如果要避免重複使用的問題，那麼就必須要加入「造幣廠」(mint) 中央控管的方式，以下是「中本聰」在該論文談到的關鍵文句。

The problem of course is the payee can't verify that one of the owners did not double-spend the coin. A common solution is to introduce a trusted central authority, or mint, that checks every transaction for double spending. After each transaction, the coin must be returned to the mint to issue a new coin, and only coins issued directly from the mint are trusted not to be double-spent. The problem with this solution is that the fate of the entire money system depends on the company running the mint, with every transaction having to go through them, just like a bank

所以、我們需要在「沒有造幣廠中央控管」的情況下，設計出一種機制，能夠讓收款人 (payee) 確定該「數位錢幣」的前一任收款人 (previous owner) 沒有重覆花用該錢幣。

We need a way for the payee to know that the previous owners did not sign any earlier transactions. For our purposes, the earliest transaction is the one that counts, so we don't care about later attempts to double-spend. The only way to confirm the absence of a transaction is to be aware of all transactions. In the mint based model, the mint was aware of all transactions and decided which arrived first. To accomplish this without a trusted party, transactions must be publicly announced, and we need a system for participants to agree on a single history of the order in which they were received. The payee needs proof that at the time of each transaction, the majority of nodes agreed it was the first received.

為了設計出這樣的機制，中本聰提出了一個採用「時間戳記伺服器」(Timestamp Server) 的辦法，該錢幣的每一手用戶都要對前一手的訊息 (包含簽章) 再進行簽章，如下圖所示：

The solution we propose begins with a timestamp server. A timestamp server works by taking a hash of a block of items to be timestamped and widely publishing the hash, such as in a newspaper or Usenet post. The timestamp proves that the data must have existed at the time, obviously, in order to get into the hash. Each timestamp includes the previous timestamp in its hash, forming a chain, with each additional timestamp reinforcing the ones before it.

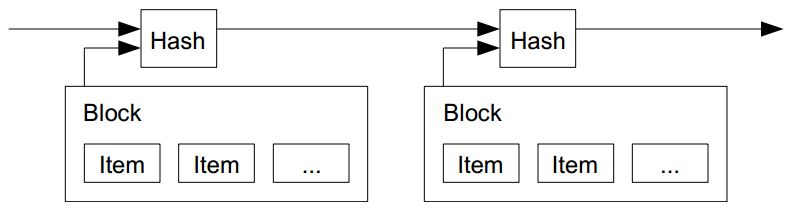
圖 2、對交易進行時間戳記的機制

圖 2、對交易進行時間戳記的機制

雜湊現金系統

但是、光有時間戳記並沒辦法解決問題，因此中本聰寫到，我們需要一個「驗證機制」 (Proof-of-Work)，這種機制採用了 Adam Back 在 Hashcash - A Denial of Service Counter-Measure (PDF, 2002) 這篇文章中所創造出的一種「雜湊現金」系統，這種系統才是虛擬貨幣的主角，而「中本聰」的主要貢獻是將 P2P 的機制引入這種「雜湊現金」系統當中，並創造出對應的程式。 。

To implement a distributed timestamp server on a peer-to-peer basis, we will need to use a proof-of-work system similar to Adam Back's Hashcash, rather than newspaper or Usenet posts.

那麼、到底 Adam Back 的論文說了些甚麼呢？其中的關鍵在於一個稱為成本函數 (Cost-Functions) 的技術上面。

成本函數 (Cost-Functions)

為了建構出一種無法否認的「數位現金」系統，必須仰賴一類稱為「成本函數」 (Cost-Functions) 的不可逆函數，這種函數「很容易驗證」(efficiently verifiable)，但是卻很難破解 (parameterisably expensive to compute)。

A cost-function should be efficiently verifiable, but parameterisably expensive to compute. We use the following notation to define a cost-function.

成本函數並非只被用在現金系統上，也可以用在對付「垃圾郵件」上，例如以下文章中就記載可用像「因數分解」這樣的問題來考驗「寄信者」 讓他們不容易到處發垃圾信，因為收信端只接受那些「通過因數分解」問題的信件，於是發垃圾郵件者就必須耗費大量的 CPU 時間去發信給這些採用 Cost-Functions 認證的人，否則信件就不會被接受。

對交互式質詢來說，因數分解足以勝任。比如，我有一個在線資源，希望您能象徵性地為其付出代價。 我可以向您發送一個消息，說“只要您能因數分解這個數，我將讓您得到這個資源”。沒有誠意的人將無法得到我的資源，只有那些能夠證明自己有足夠的興趣、付出一些 CPU 周期來回答這個質詢的人才能得到這個資源。

但是質數問題並不是最好用的，目前最常使用的 Cost-Function 是 SHA (Secure Hash Algorithm)，其運作方法如下

為了實現非交互式的“支付（payment）”，hashcash 讓我向所有想給我發送電子郵件的人都分發一個 標准質詢。在您的消息頭中，必須包括一個合法的 hashcash 戳記（hashcash stamp）；具體地說，該標志中包含我的收件人地址。

hashcash 提出質詢的方式是，當通過安全散列算法（Secure Hash Algorithm）進行散列時，要求 “minters” 生成一個字符串（戳記，stamps），在它們的散列中有很多前導零。所找到的前導零的數目就是特定戳記的比特值。 給定 SHA-1 的一致性與加密強度，找出給定比特值的 hashcash 戳記的惟一已知途徑是平均 次運行 SHA-1。

然而，要確認一個戳記，只需要進行一次 SHA-1 計算即可。對於電子郵件中的應用來說，當前推薦使用的是 20-比特值： 為了找到一個合法的戳記，發送者需要進行大約一百萬次嘗試，在最新的 CPU 和經過編譯的應用程序上，這將需要不到一秒的時間。在相對舊一些的機器上它也只需要幾秒鐘的時間。

由於 SHA 函數可以很容易的設定 b 的大小，從而可以很容易的控制該 Cost-Function 的難度，於是我門就可以指定希望耗用的 CPU 時間， 而那些願意耗用這些 CPU 時間的人，就可以透過 「CPU 時間」換取這種「數位現金」。

於是、我們就可以利用這種方式，去考驗某些人是否有足夠的「耐心」，因為這些人必須努力的用 CPU 時間去通過考驗，然後才能得到 那些「現金」(也就是某種蘿蔔或報償，像是取得寄送 email 給某人的權利，或者擁有一個比特幣的權利)。

如果您對「雜湊現金的實作技術」有興趣，可以參考筆者的另一篇文章，連結如下：

驗證系統

那麼、到底這種「雜湊現金」是如何運作的呢？後來我仔細思考，終於瞭解了其原理，而且我寫了一個採用 SHA-1 的程式，用來「雜湊出 24 bit 的前導零」 ，以下是該程式的執行結果：

D:\Dropbox\Public\web\codedata\code\sha1>gcc hashcash.c -o hashcash

D:\Dropbox\Public\web\codedata\code\sha1>hashcash
Current local time and date: Mon Dec 16 19:33:03 2013
msg=from:abc@gmail.com to:ccckmit@gmail.com title=hello! nonce=13973878
hash=00000016aa26951d1653fe515f112fe41d8ebd45
Current local time and date: Mon Dec 16 19:34:27 2013

在該程式中，我們從 nonce=0 開始尋找，希望能夠找到一個包含 nonce=數字 的樣式，可以讓 SHA-1 的雜湊值，開頭有 24bit 的前導零， 於是在經過一千三百多萬次之後，我們找到 nonce=13973878 可以滿足雜湊值有 24bit (=4*6, 6 個十六進位數字) 的前導零，也就是 下列訊息的雜湊值為 00000016aa26951d1653fe515f112fe41d8ebd45 ，滿足有 24bit 前導零的要求，所以通過了「雜湊現金」的測試。

from:abc@gmail.com to:ccckmit@gmail.com title=hello! nonce=13973878

於是我們可以將這個訊息傳送給採用「SHA-1 認證的雜湊現金」郵件收件系統，對方就可以看到訊息了！

讓我們回到中本聰的論文裏，談到如何建構「驗證系統」(proof-of-work) 的那部份，中本聰比特幣可以採用像 SHA-256 這樣的雜湊函數可以用來建立簽章鏈。

The proof-of-work involves scanning for a value that when hashed, such as with SHA-256, the hash begins with a number of zero bits. The average work required is exponential in the number of zero bits required and can be verified by executing a single hash.

但是一但簽章者找出並簽上之後，要驗證時只需要一次的 SHA 運算就行了，因此這種 「要求符合前導零數量的 SHA 運算」 完全符合上述的「成本函數」(Cost-Function) 之要求。

有了像 SHA 這類的 Cost-Function 之後，中本聰想出了一種仰賴於 CPU 總計算時間的「時間戳記系統」，這種簽章系統仰賴 SHA 中前導 0 個數 (b) 來確認該「簽章鏈」 (Block-Chain) 的文件與雜湊值是否正確，以下是「中本聰」論文中的圖片與說明：

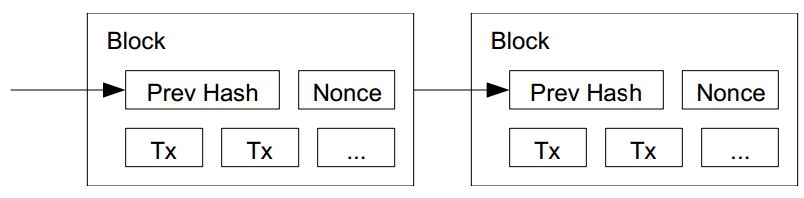
圖 3、愈往後、簽章填入愈困難的簽章鏈 (Block-Chain)

圖 3、愈往後、簽章填入愈困難的簽章鏈 (Block-Chain)

For our timestamp network, we implement the proof-of-work by incrementing a nonce in the block until a value is found that gives the block's hash the required zero bits.

接著中本聰說，如果有人想要從某節點開始偽造，就必須偽造該節點之後的所有簽章，除非他能計算的比所有其他人的總和更快，否則將無法成功的騙過大家，如下文所示：

Once the CPU effort has been expended to make it satisfy the proof-of-work, the block cannot be changed without redoing the work. As later blocks are chained after it, the work to change the block would include redoing all the blocks after it.

因此誠實的伺服器總是佔有優勢的，因為誠實者不需從頭計算起，只要忠實的將他人計算出的簽章記錄下來就行了，因此想要偽造的人通常會耗費大量的 CPU 時間，而且很難打敗誠實的伺服器。

這樣的系統也在某種程度上解決了「投票決定誰是老大」的問題，而這種投票機制是建構在「一顆 CPU 一票」的架構上，而非像網路用一個 IP 位址一票的方式。在這種架構下，誰的簽章鏈最長，誰就是擁有決定權的老大，而誠實的伺服器由於不需重新計算簽章，因此比不誠實者更具有優勢。

The proof-of-work also solves the problem of determining representation in majority decision making. If the majority were based on one-IP-address-one-vote, it could be subverted by anyone able to allocate many IPs. Proof-of-work is essentially one-CPU-one-vote. The majority decision is represented by the longest chain, which has the greatest proof-of-work effort invested in it. If a majority of CPU power is controlled by honest nodes, the honest chain will grow the fastest and outpace any competing chains. To modify a past block, an attacker would have to redo the proof-of-work of the block and all blocks after it and then catch up with and surpass the work of the honest nodes. We will show later that the probability of a slower attacker catching up diminishes exponentially as subsequent blocks are added.

The "nonce" in a bitcoin block is a 32-bit (4-byte) field whose value is set so that the hash of the block will contain a run of zeros. The rest of the fields may not be changed, as they have a defined meaning.

Any change to the block data (such as the nonce) will make the block hash completely different. Since it is believed infeasible to predict which combination of bits will result in the right hash, many different nonce values are tried, and the hash is recomputed for each value until a hash containing the required number of zero bits is found. As this iterative calculation requires time and resources, the presentation of the block with the correct nonce value constitutes proof of work.

您可以從以下這個代表 Block #274933 的比特幣區塊網頁看到，其中的 hash 值有很多個前導零，這些比特幣交易訊息的網頁可以做為進一步研究比特幣運作機制的參考。

The nonce (rhymes with once), is a user editable 4 byte field to calculate the final hash. This will typically start at 0, and for every unsuccessful hash will be incremented and hashed again. It will continue this until 2^32 numbers are checked, and if the last one is invalid, a message will be sent to the network saying the Merkle Root extended nonce needs to be increased and the whole process starts again.

So how do you determine if the hash is valid or not? The target. The final hash needs to be less than or equal to the target.

This target is the "Bits" field, only it has to be padded. However, since getting such a low target (in most cases) is so difficult, so most miners choose the largest target value they can compare to and check to see if the hash they got meets the requirements and then sends it off.

簽章與貨幣之間的關係

但是看到這裡，中本聰雖然說明了可以用 「SHA-256 雜湊現金」的方式來認證，但是這與「比特幣」之間的關係是甚麼呢？

關於這點，我在該論文裏沒有看到相關的說明語句，但是根據整個論文的邏輯，我的理解推論如下：

假如每填入一個簽章，就可以獲得一枚比特幣，那麼所有人就都要努力的去填入簽章，以便獲得比特幣。

但是這樣有個問題，一開始沒有任何比特幣，因此也就沒有任何的「交易」，沒有交易的話那就不需要簽章了，所以這世界上根本就不會有這樣的貨幣存在啊。

因此、系統必須採用某些貨幣產生策略，穩定的產生一些比特幣作為那些建立伺服器讓比特幣系統運作起來的網站之報酬。

中本聰稱這種報酬為 Incentive (獎勵)。

於是中本聰寫到：

By convention, the first transaction in a block is a special transaction that starts a new coin owned by the creator of the block. This adds an incentive for nodes to support the network, and provides a way to initially distribute coins into circulation, since there is no central authority to issue them. The steady addition of a constant of amount of new coins is analogous to gold miners expending resources to add gold to circulation. In our case, it is CPU time and electricity that is expended.

當然、這種獎勵機制應該是公開透明、而且可以被所有伺服器計算出來的，否則就會有些伺服器亂給自己獎勵了。

有了這種獎勵機制之後，就能解決「一開始沒有任何比特幣」的問題，於是整個系統就可以完整的運作了。

為何「比特幣挖礦」越來越難？

當這些獎勵注入系統時，就有可能開始進行交易了，有了交易，那麼就會產生如圖 1 所示的交易鏈，而這些交易鏈需要簽章以避免 被惡意竄改 (如圖 2)，而那些幫忙計算簽章的人又可以獲得一些比特幣，於是比特幣就會越來越多。

但是這並不能說明為何 2010 年時挖比特幣很容易，2013 年的現在卻很難，因此還有一些疑點待查證的，

說明：我猜測「比特幣」一開始時，前導零的長度可能很小，貨幣發行率 (Incentive, 獎勵) 也比較高，但是隨著時間與挖掘的數量，筆者推測貨幣發行率將會降低，而且前導零的長度應該會隨之增加， 也就是 b 的値會越來越大，於是想要找出符合這種 b 個前導零的 SHA 雜湊值就會越來越難了 (因為要花費 次 SHA 運算)，這應該也就是比特幣之所以越來越難挖的原因了。

研讀至此，我大概已經理解了比特幣的運作原理，剩下的就是整個「貨幣系統」的建構細節考量了！

在論文的後半段，中本聰說明了這種「比特幣網路」的建構與訊息流通原理，另外還透過「布瓦松分布」(Poisson Distribution) 去分析 比特幣被駭客攻擊，導致某些簽章鏈被修改的機率。對於這部份有興趣的朋友就請直接看原始論文囉！

但是、在讀完中本聰的比特幣論文之後，筆者仍然有個疑問，現行比特幣的「獎勵公式」到底是甚麼呢？中本聰在論文裏好像沒有提出說明！

後記

這篇文章是筆者研讀「中本聰」的比特幣論文 Bitcoin: A Peer-to-Peer Electronic Cash System 的筆記，一開始筆者完全不瞭解這個領域的技術，研讀時也沒辦法徹底理解文中很多技術的意義，還好筆者有點密碼學的概念，因此稍微可以讀懂。

於是當我寫了「初稿」之後就在 自己的 facebook 上 與 程式人雜誌社團 裏分享給網友看，結果看的人還不少，甚至有些網友還指出文章中的一些問題，像是有人說「比特幣不是採用 SHA-256 嗎？」，於是筆者查證之後發現確實是 SHA-256，因此趕緊更正，然後又有網友發現我對 nonce 的解釋有問題，因此說：「至少 nonce 的運作方式說明錯了, 公開的發表要小心!」，而且還告訴我們「 https://blockchain.info/ 可以查到比特幣的立即資訊」，這讓筆者可以透過觀察「比特幣交易」更進一步瞭解比特幣的運作方式。

筆者並非很嚴謹的人，而且很喜歡分享文章，因此往往在文章寫好後就分享出去。在這篇文章的分享過程中，我發現了這種「早期就分享文章」的撰寫方式，其實有點像 Linux 這種開放原始碼軟體的建構方式，透過不斷的修改與分享，可以讓「讀者與作者」隨時進行交流，於是「程式與文章」都可以透過這種交流逐漸成熟。

在開放原始碼領域，領域裏的 Eric Steven Raymond 曾經寫過一篇稱為「 大教堂和市集 」的經典文章，將傳統軟體開發隱喻為「大教堂模式」，而開放原始碼像 Linux 這樣的系統開發則隱喻為「市集模式」。

結果 Eric Steven Raymond 發現市集模式其實也可以做出很好的軟體，像是 Linux 等這樣大型的作業系統，也可以透過市集模式建構出來。

而在這篇文章的撰寫過程當中，我們也發現採用「類似市集模式」的方法，我們也可以用在寫作文章上面。未來或許會有些偉大的文章或書籍，是採用市集模式撰寫出來的也說不定呢？ (其實、維基百科就是這樣一個範例，不是嗎？)

參考文獻

【本文由陳鍾誠取材並修改自 維基百科，採用創作共用的 姓名標示、相同方式分享 授權】