數學短訊:邏輯世界的歷史
簡介
邏輯學是西方科學中淵遠流長的一門學問,從西元前 350 年亞里斯多德的三段論開始,就開啟了歐洲文明對邏輯學的興趣之窗。然而這一個興趣同樣隨著西方文明的發展而起伏不定,直到西元 1850 年左右,George Boole (布爾) 開始研究布林代數,才讓邏輯學成為近代數學的一個重要領域。接著,Gottlob Frege 在 1870 年左右所提出的一階邏輯系統,繼承布林系統並向上延伸,形成一個數學基礎穩固且強大的邏輯系統,於是整個經典的邏輯系統建立完成。
雖然如此,這些邏輯系統仍然是掌上的玩物,而且沒有人能確定這樣的邏輯系統,其能力到底有多強,是否一致且完備,是否有某些極限。希爾伯特在 1900 年所提出的 25 個數學問題中,這個問題被排在第二個提出。然而,希爾伯特並沒有能證明一階邏輯系統的完備性,而是在 1929 年由哥德爾證明完成了。
哥德爾的成就不僅於此,1931 年他更進一步證明了一個非常令人驚訝的定理,在「一階邏輯的擴充系統 - 皮諾數論系統」當中,不具有完備性,而且它證明了假如該系統是完備的,將會導致矛盾。
哥德爾在證明完備定理與不完備定理時,採用的都是矛盾証法,也就是透過排中律所證明的,這樣的証明並非建構性的,因此即使建立了完備定理,也沒有人能構造出一個建構式的証明方法,可以檢證一階邏輯的定理。
1965 年,Robinson 提出了一條非常簡單的邏輯證明規則 -- Resolution,並且說明了如何利用矛盾檢證程序 Refutation,證明邏輯規則在某系統中的真假,這個方法既簡單又優美,因此廣為數學界與計算機科學界所稱道。以下,我們將更詳細的說明上述人物在邏輯學上的貢獻。
亞里斯多德 (Aristotle) (出生於西元前 322 年)
亞里斯多德在其其理則學 (zoology) 研究中,提出了下列的三段式推論規則 Barbara,簡稱為三段論。
| 類型 | 語句 | 說明 |
|---|---|---|
| 大前提 | 所有人都終會死亡 | 普遍原理 |
| 小前提 | 蘇格拉底是人 | 特殊陳述 |
| 結論 | 蘇格拉底終會死亡 | 推論結果 |
布爾 (Boole) (出生於 1815年)
Boole 研究邏輯時,提出了一種只有真值與假值的邏輯,稱為二值邏輯,通常我們用 0 代表假值,1 代表真值。布爾研究這種邏輯系統,並寫出了一些代數規則,稱為布林代數,以下是其中的一些代數規則。
| 規則 (數學寫法) | 名稱 |
|---|---|
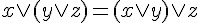 |
OR 的結合律 |
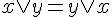 |
OR 的交換律 |
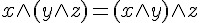 |
AND 的結合律 |
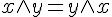 |
AND 的交換律 |
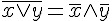 |
狄摩根定律(1) |
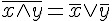 |
狄摩根定律(2) |
說明:上述規則中的 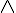 代表邏輯或 (AND) (在程式語言裏常寫為
代表邏輯或 (AND) (在程式語言裏常寫為 & 或 and), 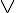 代表邏輯或 (OR) (在程式語言裏常寫為
代表邏輯或 (OR) (在程式語言裏常寫為 | 或 or)。所以若改用程式領域的寫法,可改寫如下。
| 規則 (數學寫法) | 名稱 |
|---|---|
x | (y | z) = (x | y) | z |
OR 的結合律 |
x | y = y | z |
OR 的交換律 |
x & (y & z) = (x & y) & z |
AND 的結合律 |
x & y = y & x |
AND 的交換律 |
-(x|y) = -x & -y |
狄摩根定律(1) |
-(x&y) = -x | -y |
狄摩根定律(2) |
福雷格 (Frege) (出生於 1848年)
Frege 在研究邏輯系統時,將函數的概念引入到邏輯系統當中,這種函數被稱為謂詞,因此該邏輯系統被稱為謂詞邏輯。然後,Frege 又引入了兩個量詞運算, 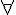 (對於所有) 與
(對於所有) 與 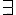 (存在),透過謂詞的限定作用,以及這兩個量詞,Frege 架構出了這種具有函數的邏輯系統,後來被稱為一階邏輯系統 (First Order Logic)。
(存在),透過謂詞的限定作用,以及這兩個量詞,Frege 架構出了這種具有函數的邏輯系統,後來被稱為一階邏輯系統 (First Order Logic)。
以下是我們將亞里斯多德的三段論,轉化為一階邏輯後,所寫出的一階邏輯規則。
| 類型 | 語句 | 說明 |
|---|---|---|
| 大前提 | 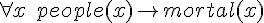 |
所有人都終會死亡 |
| 小前提 | 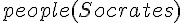 |
蘇格拉底是人 |
| 結論 | 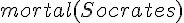 |
蘇格拉底終會死亡 |
希爾伯特 (David Hilbert) (出生於 1862年)
事實上,在電腦被發明之前,數學界早已開始探索「公理系統」的能力極限。在西元 1900 年時,德國的偉大數學家希爾伯特 (Hilbert),提出了著名的 23 個數學問題,其中的第二個問題如下所示。
證明算術公理系統的無矛盾性 The compatibility of the arithmetical axioms.
在上述問題中,希爾伯特的意思是要如何證明算術公理系統的 Compatibility,Compatibility 這個詞意謂著必須具有「一致性」 (Consistency) 與「完備性」(Completeness)。
所謂的「一致性」,是指公理系統本身不會具有矛盾的現象。假如我們用 A 代表該公理系統,那麼 A 具有一致性就是 A 不可能導出兩個矛盾的結論,也就是 A => P 與 A=> -P 不可能同時成立。
所謂的「完備性」,是指所有「永遠為真的算式」(也就是定理) 都是可以被証明的,沒有任何一個定理可以逃出該公理系統的掌握範圍。
然而,希爾伯特耗盡了整個後半生,卻也無法證明整數公理系統的一致性與完備性。或許是造化弄人,這個任務竟然被希爾伯特的一位優秀學生 - 哥德爾 (Godel) 所解決了,或者應該說是否決了。
哥德爾 (Kurt Gödel) (出生於 1906 年)
哥德爾實際上證明了兩個定理,第一個是 1929 年提出的「哥德爾完備定理」(Gödel's Complete Theorem),第二個是 1931 年證明的「哥德爾不完備定理」(Gödel's Incomplete Theorem),這兩個定理看來似乎相當矛盾,但事實上不然,因為兩者所討論的是不同的公理系統,前者的焦點是「一階邏輯系統」(First Order Logic),而後者的焦點則是「具備整數運算體系的一階邏輯系統」。
哥德爾完備定理證明了下列數學陳述:
一階邏輯系統是一致且完備的
一致性代表一階邏輯系統不會具有矛盾的情況,而完備性則說明了一階邏輯當中的所有算式都可以被証明或否証。
哥德爾不完備定理證明了下列數學陳述:
任何一致且完備的「數學形式化系統」中,只要它強到足以蘊涵「皮亞諾算術公理」,就可以在其中構造在體系內「既不能證明也不能否證的命題」。
哥德爾不完備定理改用另一個說法,如下所示:
如果一個包含算術的公理系統可以用來描述它自身時,那麼它要麼是不完備的,要麼是不一致的,不可能兩者皆有!
(筆者註:若該公理系統包含無限條公理時,必須是可列舉的 recursive enumerable)
羅賓遜 (John Alan Robinson) (出生於 1928 年)
雖然哥德爾證明了一階邏輯是完備的,但是卻沒有給出一個建構式的方法,可以推理出所有的的一階邏輯定理。這個問題由 John Alan Robinson 在 1965 年解決了。
Robinson 提出的 refutation 邏輯推論法是一種反證法,任何一階邏輯的算式 P 只要在系統 S 當中是真的,只要將 -P 加入該系統 S 中,就可以經由反證法導出矛盾。如果 P 在系統 S 當中不是真的,那麼將 P 加入 S 當中就無法導出矛盾。
所謂的 refutation 反證法是依靠一個稱為 resolution 的邏輯規則,該規則如下所示:
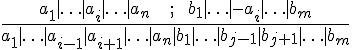
假如我們將上述算式中的 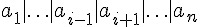 寫為 A,將
寫為 A,將 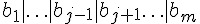 寫為 B,則上述算式可以改寫如下:
寫為 B,則上述算式可以改寫如下:
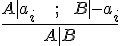
結語
邏輯學在西方文化中扮演了非常重要的角色,而且可以說是「現代科學」會出現在歐洲的重要原因,假如將「邏輯學」從西方文化中拿掉,或許工業革命就不會出現在歐洲了?
您可以想像「孔子」整天追根究柢,常常和人辯論一件事情到底是真的還假,而且要轉換成符號,並且用邏輯的方式去證明嗎?
但是「亞里斯多德」在那個年代就是這樣追根究柢的,所以他才會去研究解剖學,把動物給切開看看裡面有甚麼,我想這也是他提出三段論背後的原因吧!
參考文獻
- 維基百科:亞里斯多德
- 維基百科:喬治·布爾
- 維基百科:三段論
- 維基百科:哥德爾不完備定理
- 維基百科:哥德爾完全性定理
- 維基百科:戈特洛布·弗雷格
- 維基百科:大衛·希爾伯特
- 維基百科:希爾伯特的23個問題
- 維基百科:庫爾特·哥德爾
- Wikipedia:Zoology
- Wikipedia:Aristotle
- Wikipedia:Boolean Logic
- Wikipedia:George Boole
- Wikipedia:Frege
- Wikipedia:Hilbert's_problems
- Wikipedia:John Alan Robinson
- Wikipedia:Resolution (Logic)
- Hilbert's Mathematical Problems
- Wikipedia:Kurt_Gödel
【本文由陳鍾誠取材並修改自 維基百科,採用創作共用的 姓名標示、相同方式分享 授權】