布林邏輯與推論系統 -- 何謂嚴格的數學證明？
前言
當我還是個學生時，我總是困惑著如何應付老師的考試，其中一個重要的數學困擾是，老師要我們「證明」某個運算式。
最大的問題不在於我不會「證明」，因為在很多科目的證明題當中，我也都「答對了」，但是這種答對總是讓我感到極度的沒有把握，因為有時老師說「這樣的證明是對的」，但有時卻說「這樣的證明是錯的」。
更神奇的是，老師的證明永遠都是對的，他們可以突然加入一個「推論」，而這個推論的根據好像之前沒有出現過，然後他們說：「由此可證」、「同理可證」....。
直到有一天，我終於懂了。
因為課堂上老師的證明往往不是「嚴格的證明」，因為嚴格的證明通常「非常的困難」，每個證明都可以是一篇論文，甚至在很多論文當中的證明也都不是嚴格的。
所以在課堂上，老師總是可以天外飛來一筆的，跳過了某些「無聊的步驟」，奇蹟式的證明了某些定理，而這正是我所以感到困擾的原因。
一般的證明
一般而言，日常生活中的證明，通常是不嚴格的。
舉例來說，我可以「證明」某人殺了死者，因為殺死死者的兇刀上有「某人」的指紋。
但是這樣的證明並不嚴格，因為有很少的可能性是「某人摸過兇刀、但是並沒有殺人」。
所以我們總是可以看到那個「外表看似小孩，智慧卻過於常人」的「名偵探柯南」，總是天外飛來一筆的「證明」了某人是兇手，這種證明與數學證明可是完全不同的。
嚴格的證明
數學的證明通常不能是「機率式」的，例如：「我證明他 99% 殺了人」，這樣的證明稱不上是嚴格的證明。
嚴格的證明也並非結果一定要是 100% 的正確 (當然也不是說結果不正確)，真正的證明是一種過程，而不是結果。
怎麼說呢？
數學其實很像程式領域的演算法，或者就像是電腦的運作過程，當我們設計出一顆 CPU 之後，你必須用該 CPU 的指令撰寫出某些函數，以便完成某個程式。
那麼，數學的 CPU 是甚麼呢？
答案是「公理系統」 (Axioms)！
只有透過公理系統，經由某種演算方式，計算出待證明定理在任何情況下都是真的，這樣才算是證明了該定理。
這些公理系統其實就是數學的 CPU 指令集。
布林代數大概是數學當中最簡單的系統了，因為布林代數的値只有兩種--「真與假」 (或者用 0 與 1 代表)。
為了說明嚴格的數學證明是如何進行的，我們將從布林代數的公理系統 (CPU?) 開始，說明如何證明布林代數的某些定理，就好像是如何用指令集撰寫程式一樣。
布林邏輯
對於單一變數 x 的布林系統而言，x 只有兩個可能的值 (0 或 1)。
對於兩個變數 x, y 的布林系統而言，(x, y) 的組合則可能有 (0,0), (0,1), (1,0), (1,1) 四種。
對於三個變數 x, y, z 的布林系統而言，(x, y, z) 的組合則可能有 (0,0, 0), (0,0,1), (0,1,0), (0,1,1), (1,0, 0), (1,0,1), (1,1,0), (1,1,1) 八種。
基本的布林邏輯運算有三種，AND (且), OR (或), NOT (反)，在布林代數當中，通常我們在符號上面加一個上標橫線代表 NOT，用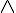 
代表 AND，用 
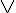代表 OR。
但是在程式裏面，受到 C 語言的影響，很多語言用驚嘆號 ! 代表 NOT，用 & 代表 AND，用 | 代表 OR。以下我們將採用類似 C 語言的程式型寫法進行說明。
| NOT | AND | OR | ||||||||||||||||||||||||||||||||||||
|
|
|
假如我們想知到某個邏輯式的真值表，例如 (-x | y) 的真值表，只要透過列舉的程序就可以檢查完畢。
| x | y | -x | -x|y |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 |
接著，我們就可以定義一些公理系統，這些「公理系統」就像是數學推理的指令集，讓我們可以推論出哪些邏輯式在這個公理系統下是真的 (定理)，哪些邏輯式這個公理系統下不一定是真的。
公理系統 1
舉例而言，假如我們制定了一個公理系統如下所示。
公理 1: -p | q
公理 2: p那麼，我們就可以列出這個布林系統的真值表。
| p | q | -p|q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
在上述真值表中，凡是無法滿足公理系統的列，就代表該項目違反公理系統，因此在此公理系統下不是真的，可以被刪除 (不是該公理系統的一個「解答」)。
註：在邏輯的術語中，滿足該公理系統的解答，稱為一個 Model (模型)。
在上述表格中，前兩條的 x 為 0，因此不滿足公理 2，而第三條的 -p|q 為 0，不滿足公理 1，因此符合該公理系統的項目就只剩下了一個了。
| p | q | -p|q |
|---|---|---|
| 1 | 1 | 1 |
在這個滿足公理系統的真值表當中，我們可以看到 q 只能是 1，也就是 q 其實是個定理。
說明：在上述邏輯推論系統當中， -p|q 可以簡寫為 p → q，因此上述公理系統可以改寫如下，這樣的推論法則稱為 Modus Ponus (中文翻成「肯定前件」)。
公理 1: p → q
公理 2: p
------------------
結論： q公理系統 2
假如我們定義了以下的公理系統：
公理 1: -p | q
公理 2: p | r那麼我們可以列出真值表如下：
| p | q | r | -p|q |
p|r |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
當我們將不符合公理系統的項目拿掉之後，以上的真值表就只剩以下這些項目。
| p | q | r | -p|q |
p|r |
|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
此時，如果我們檢查這些項目中 q|r 的真值表，會發現 q|r 為真者其結果全部為 1 ，因此 q|r 在這個公理系統下是真理。
| p | q | r | -p|q |
p|r |
q|r |
p|q |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
但是如果我們檢查這些項目中 p|q 的真值表，會發現有一項為 0 ，因此 p|q 在這個公理系統下並非真理。
所以 q|r 在此公理系統下是一個定理，但 p|q 則不是定理。
說明：在上述邏輯推論系統當中， -p|q 可以簡寫為 p → q，而 p|r 則可以想成 -(-p)|r ，於是寫成 -p → r。
於是您可以觀察到當 p=1 時 q=1，當 p=0 時 r=1，而 p 只有可能是 1 或 0，於是 q 與 r 兩者至少有一個成立，這也就是推論出的定理 q|r 成立的原因了。
推論法則
現在，我們已經具備了足夠的基本知識，可以用來說明何謂嚴格的數學證明了。
假如我們將公理系統 2 中推論出 q|r 的程序，變成一條明文的規則，如下所示：
(-p | q) & (p | r) → (q|r)那麼，我們就可以用這樣的規則進行推論，這個推理方式乃是 Robinson 所提出的，稱為 Resolution 法則。
於是我們可以根據這條規則，推論出某個邏輯公理系統下的定理。
必須注意的是，在以上的描述中，我們並沒有區分變項與常項。讓我們在此先說明一下。
在一般的邏輯系統中，通常我們用小寫代表變項，大寫代表常項。其中的變項可以設定成任意的項目，而常項則只能代表自己。
舉例而言，A, B, C, DOG, SNOOPY 等代表常項，而 x, y, z, w, .... 等則代表變項。
公理系統理可以包含變項與常項，舉例而言，假如有個公理系統如下所示。
A | -B
-A | C
-(-B | C) | D而這整個邏輯系統的推論法則只有一條，那就是 Resolution 法則，也就是 (-p | q) & (p | r) → (q|r) 。
我們可以透過推論法則對公理系統中的公理進行綁定 (例如 p 設定為 A，q 設定為 -B ....) 與推論，得到下列結果：
(A | -B) & (-A | C) → (-B|C) ; 令 p=A, q=-B, r=C ，於是可以推出 (-B|C)。
(-B|C) & (-(-B | C) | D) → D ; 令 p=(-B|C), q=D, r=空集合，於是可以推出 D。透過這樣的推論、我們就得到了以下的「事實庫」。
A | -B
-A | C
-(-B | C) | D
(-B | C)
D如此我們就可以不需要依靠真值表，直接從公理系統開始，透過嚴格的計算程序，推論出該公理系統中的定理了。
這種證明方式，就是一種為嚴格的數學證明。
這種證明所遵循的，乃是一種 『公理 / 推論 / 定理1 / 推論 / 定理2 / ...』 的方式，這種方式讓證明變成了一種計算過程，是可以寫成電腦程式的，這種證明方式乃是一種嚴格可計算的證明方式。
後記
大部分的數學系統，都希望能達到這樣嚴格的程度，但可惜的是，並非所有數學系統都能完全達到這樣嚴格的程度。舉例而言：歐氏幾何可以說是公理化的早期經典之作，但其中仰賴圖形直覺的證明過程仍然有很多，並非完全達到公理化。而微積分等數學的嚴格公理化也一直是數學家還在研究的問題。
但對公理化數學體系最精彩的一段歷史是，希爾伯特對公理化的問題與歌德爾不完備定理對數學可完全公理化的反證，以下是這段歷史的簡要說明。
20 世紀的大數學家 Hilbert 曾經於 1900 年提出的 23 個數學問題中提到一個問題，就是「是否能為數學系統建立證明法則，讓數學證明可以完全被計算出來」，後來歌德爾 (Godel) 在 1926 年證明了一階邏輯的完備定理，讓大家看到了一線曙光，但歌德爾在 1929 年又提出了一個數論系統的不完備定理，證明了有些定理無法透過計算程序證明。
歌德爾的研究，後來在電腦領域，被圖靈 (Turing) 重新詮釋了一遍，圖靈證明了「停止問題」是電腦無法 100% 正確判定的問題，這也開啟了後來計算理論的研究之河。圖靈也因此而成為計算理論領域的第一人，所以 ACM 這個組織才會將電腦界的最重要獎項稱為「圖靈獎」(Turing Award)。
參考文獻
- 維基百科：命題邏輯
- 相關討論：為甚麼國中的數學證明是從「歐式幾何」開始教，而不從「布林代數」開始教呢？
- 數學中的公理化方法 (上) 吳開朗
- 數學中的公理化方法 (下) 吳開朗
【本文由陳鍾誠取材並修改自 維基百科，採用創作共用的 姓名標示、相同方式分享 授權】