前言
編輯小語
在本期的「程式人雜誌」中,聚焦的主題是「神經網路」,包含理論與實作!
神經網路是「機器學習」與「人工智慧」中的一個重要方法,常被用在「影像處理、語音處理、分群分類」等領域。
雖然神經網路有很多種類,但本期關注的主要技術是「感知器」,包含「單層感知器」與「多層感知器」,以及用在「多層感知器」上的「反傳遞學習演算法」。
當然、本期不只有「神經網路」的相關文章,還有更精彩的 Arduino, VB, OpenNI, 開放電腦計畫等內容,希望讀者會喜歡這期的「程式人雜誌」!
---- (程式人雜誌編輯 - 陳鍾誠)
授權聲明
本雜誌許多資料修改自維基百科,採用 創作共用:姓名標示、相同方式分享 授權,若您想要修改本書產生衍生著作時,至少應該遵守下列授權條件:
- 標示原作者姓名 (包含該文章作者,若有來自維基百科的部份也請一併標示)。
- 採用 創作共用:姓名標示、相同方式分享 的方式公開衍生著作。
另外、當本雜誌中有文章或素材並非採用 姓名標示、相同方式分享 時,將會在該文章或素材後面標示其授權,此時該文章將以該標示的方式授權釋出,請修改者注意這些授權標示,以避免產生侵權糾紛。
例如有些文章可能不希望被作為「商業性使用」,此時就可能會採用創作共用:姓名標示、非商業性、相同方式分享 的授權,此時您就不應當將該文章用於商業用途上。
最後、懇請勿移除公益捐贈的相關描述,以便讓愛心得以持續散播!
本期焦點
神經網路簡介
在電腦領域,神經網路是指一種模擬神經系統所設計出來的程式,用來模擬人類視覺、聽覺等等智慧行為的原理,企圖讓電腦可以具有人類智慧的一種方法。
下圖是生物神經細胞的結構圖,這個圖看來頗為複雜,如果電腦程式真的要模擬這麼複雜的結構,那程式應該也會非常複雜才對。
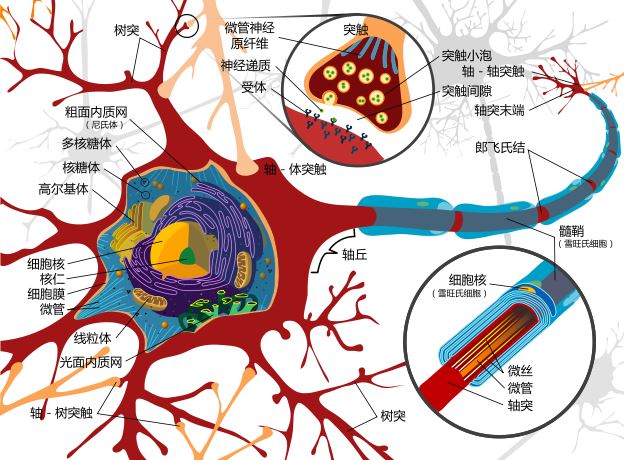
圖、神經細胞的結構
還好、神經網路程式不需要去模擬「細胞膜、粒線體、核醣體」等等複雜的結構,因為學電腦的人可以透過「抽象化」這個伎倆,將上述的神經細胞結構簡化成下圖 (a) 的樣子。
在下圖中,a1 ... an 是輸入,w1 ... wn 是權重,這些輸入乘上權重之後加總(SUM),就會得到神經元的刺激強度,接著經過函數 f() 轉換之後,就得到了輸出的刺激強度。
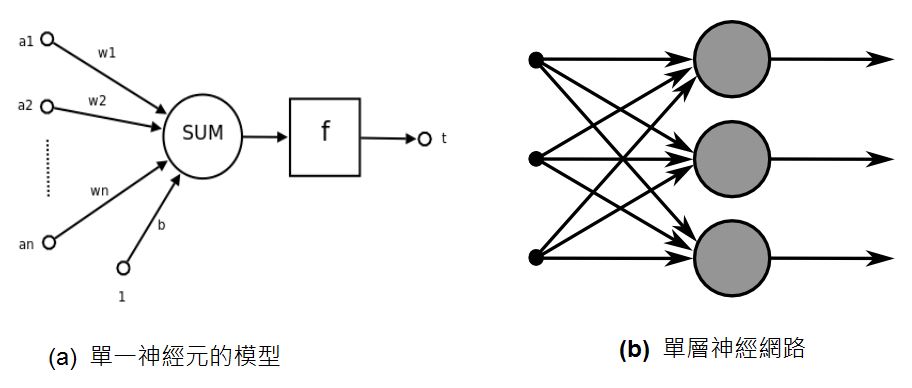
圖、神經網路連接模型
上圖 (a)所對應的數學公式如下:
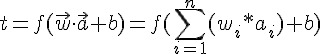
其中的 b 值是用來作為門檻的閥值,舉例而言,若 b 是 -0.5,那麼就代表要將總合減掉 0.5,才得到輸入刺激強度,這可以用來調節刺激強度,才不會一直增強上去。
而上圖 (b) 中的網路,是一種單層的神經網路,所謂單層是不計算輸入節點的計算方式,因此只有圖中的大圈圈才算是一層,其中每個大圈圈都是如圖 (a) 中的一個神經元。
最早的神經網路程式稱為感知器(Perceptron),這是由 Frank Rosenblatt 在 1957 年於 Cornell 航空實驗室 (Cornell Aeronautical Laboratory) 所發明的。
但是在 1969 年,Marvin Minsky 和 Seymour Papert 在《Perceptrons》書中,仔細分析了知器為的功能及局限,證明感知器不能解決簡單的 XOR 等問題,結果導致神經網路技術經歷了長達 20 年的低潮期。
後來在 1986 年,Rumelhart 等人於下列論文中提出「反向傳播」(back-propagation) 演算法,並成功的被運用在語音辨識等領域之後,神經網路才又開始成為熱門的研究主題。
Rumelhart, David E.; Hinton, Geoffrey E., Williams, Ronald J. Learning representations by back-propagating errors. Nature. 8 October 1986, 323 (6088): 533–536.
事實上、反向傳播的方法,並不是 Rumelhart 等人第一個提出來的,Paul J. Werbos 1974 年在哈佛的博士論文中就提出了類似的方法,只是大家都不知道而已。
Paul J. Werbos. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. PhD thesis, Harvard University, 1974
當然、神經網路再度成為研究焦點之後,各式各樣的方法又被發展出來了,大致上這些方法可以分為兩類,一種稱為「有指導者」的神經網路(Supervised Neural Network) ,像是「感知器與反傳遞演算法」等,另一種稱為「沒有指導者」的神經網路 (Unsupervised Neural Network),像是「霍普菲爾德網路 (Hopfield Network) 與自組織神經網路 (Self Organization network)」等等。
當然、神經網路並不是「神奇銀彈」,可以解決人工智慧上的所有問題,神經網路最強大的地方是容錯性很強,而且不需要像專家系統這樣撰寫一堆規則,但是有一得必有一失,神經網路自動學習完成之後,我們根本不知道該如何再去改進這個學習成果,因為那些權重對人類來說根本就沒有什麼直觀的意義,因此也就很難再去改進這個網路了。
不過、程式能夠自我學習畢竟是一件很神奇的事情,光是這點就值得讓我們好好的去瞭解一下神經網路到底是怎麼運作的了!
參考文獻
- Wikipedia:Neuron
- Wikipedia:Artificial neuron
- Wikipedia:Artificial neural network
- Wikipedia:Perceptron
- Wikipedia:Backpropagation
- 維基百科:感知器
- 維基百科:人工神經網路
- 維基百科:赫布理論
【本文由陳鍾誠取材並修改自 維基百科,採用創作共用的 姓名標示、相同方式分享 授權】
單層感知器 (Perceptron) 實作 - 使用 JavaScript+Node.js
簡介
Rosenblatt 於 1958 年提出第一個神經網路模型,稱為感知器,這個模型是基於 1943 年 McCulloch 與 Pitts 所提出的神經元模型,該模型的數學公式如下。
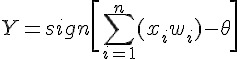
其中的 sign 是正負號判斷函數,若是正數則傳回 1,負數則傳回 0。
請注意,在此我們所說的「感知器」是指 Rosenblatt 當時所使用的感知器,特指只有一層節點的「單層感知器」,而不是指稱那種具有隱藏層的「多層感知器」(Multilayer Perceptron),這點必須特別澄清一下!
而所謂感知器的學習,就是透過調整權重 wi 的方式,讓整個網路可以學到某個函數的方法,所以權重的調整方法是整個感知器學習行為的核心。
感知器的學習
那麼、我們要怎麼讓神經網路學會某個函數呢?以下是感知器學習的演算法:
初始化:設定權重
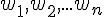 和臨界值
和臨界值 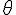 的初值之範圍為 [-0.5, 0.5]。
的初值之範圍為 [-0.5, 0.5]。激勵:用輸入
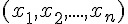 、權重
、權重 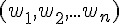 與閥值
與閥值 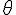 計算感知器的輸出值 Y。
計算感知器的輸出值 Y。權重修改:根據函數輸出 Yd 與感知器輸出 Y 之間的差異,進行權重調整。
3.1 計算誤差 :
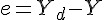
3.2 計算調整量:
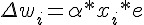
3.3 調整權重 :
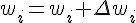
重複 2-3 步驟,直到學會為止 (如果一直學不會,只好宣告失敗)。
感知器模型 (兩個輸入的情況)
根據以上的方法,假如感知器的輸入只有兩個 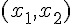 那麼權重也只會有兩個
那麼權重也只會有兩個 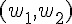 ,於是我們可以得到下列的感知器模型:
,於是我們可以得到下列的感知器模型:
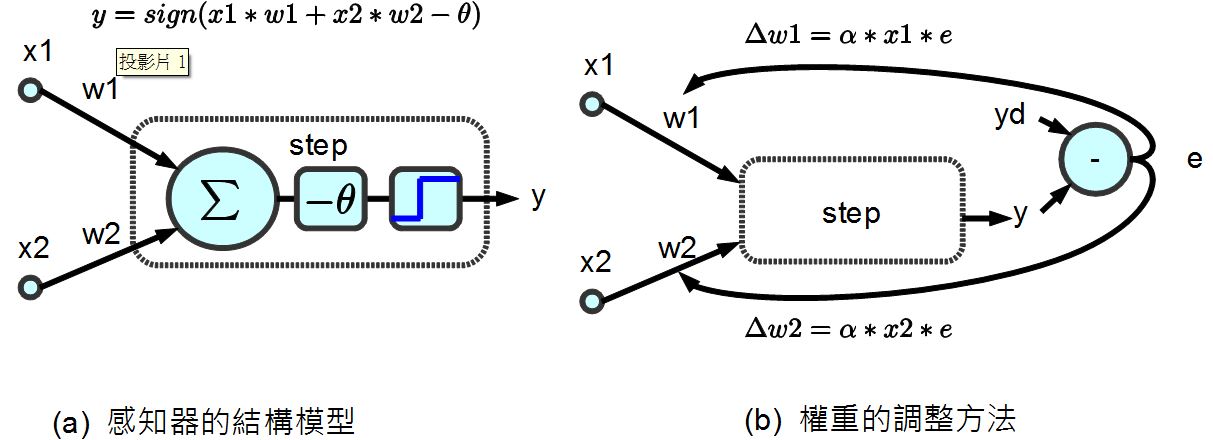
圖、兩個輸入的感知器模型
假如我們的目標函數對於某組 (x1, x2) 的期望輸出為 yd,那麼就可以計算出誤差為 e=yd-y,於是我們可以透過下列方法調整權重。
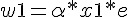
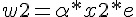
可惜的是、上述的調整方法中,並沒有調整到 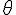 值,如果我們想要連
值,如果我們想要連 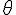 值也一並設計成可浮動的,那麼就可以將
值也一並設計成可浮動的,那麼就可以將 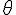 加入到 w 中,成為 w0,,並將 x0 設為 -1,如下圖所示:
加入到 w 中,成為 w0,,並將 x0 設為 -1,如下圖所示:
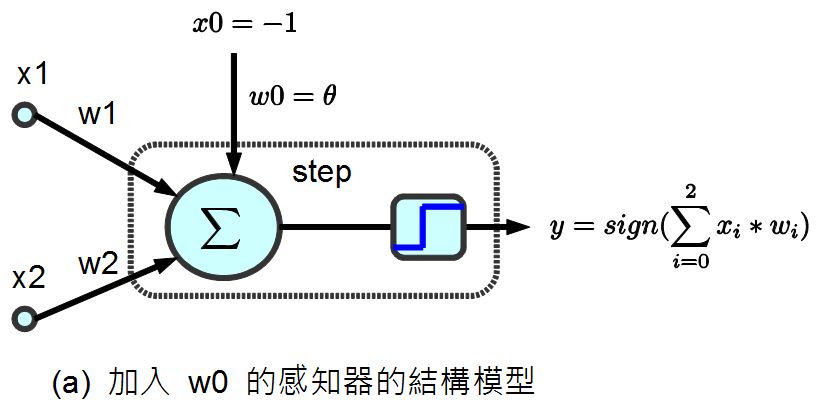
圖、調整簡化後的感知器模型
經過上述的調整簡化之後,我們只要在調整權重時加入下列這條,就可以連 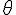 也一併調整了。
也一併調整了。
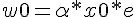
當我們對某布林函數「真值表」中的每一個輸入,都反覆進行上述調整,最後是否能學會該「布林函數」呢?
那麼、我們是否能夠用這麼簡單的方法讓感知器學會 AND、OR 與 XOR 函數呢?
如果可以的話,那麼我們能不能擴大到 n 輸入的感知器上,讓感知器學會任何一個布林函數呢?
如果感知器可以學會任何一個布林函數,那就會具有強大的威力了!
但可惜的是,這個問題的答案是否定的,雖然感知器可以學會 AND 與 OR,但是卻不可能學會 XOR 函數。
在說明這個問題的理論之前,先讓我們透過實作來體會一下感知器是如何學習 AND 與 OR 函數的,然後感受一下感知器在學 XOR 函數時發生了甚麼問題?
等到瞭解了程式的運作原理之後,我們再來說明為何感知器無法學會 XOR 函數。
感知器實作
以下我們使用 JavaScript 程式實作出感知器,其程式碼如下,您可以在 node.js 環境下執行此一程式:
檔案:perceptron.js
var log = console.log;
var Perceptron = function() { // 感知器物件
this.step=function(x, w) { // 步階函數:計算目前權重 w 的情況下,網路的輸出值為 0 或 1
var result = w[0]*x[0]+w[1]*x[1]+w[2]*x[2]; // y=w0*x0+x1*w1+x2*w2=-theta+x1*w1+x2*w2
if (result >= 0) // 如果結果大於零
return 1; // 就輸出 1
else // 否則
return 0; // 就輸出 0
}
this.training=function(truthTable) { // 訓練函數 training(truthTable), 其中 truthTable 是目標真值表
var rate = 0.01; // 學習調整速率,也就是 alpha
var w = [ 1, 0, 0 ];
for (var loop=0; loop<1000; loop++) { // 最多訓練一千輪
var eSum = 0.0;
for (var i=0; i<truthTable.length; i++) { // 每輪對於真值表中的每個輸入輸出配對,都訓練一次。
var x = [ -1, truthTable[i][0], truthTable[i][1] ]; // 輸入: x
var yd = truthTable[i][2]; // 期望的輸出 yd
var y = this.step(x, w); // 目前的輸出 y
var e = yd - y; // 差距 e = 期望的輸出 yd - 目前的輸出 y
eSum += e*e; // 計算差距總和
var dw = [ 0, 0, 0 ]; // 權重調整的幅度 dw
dw[0] = rate * x[0] * e; w[0] += dw[0]; // w[0] 的調整幅度為 dw[0]
dw[1] = rate * x[1] * e; w[1] += dw[1]; // w[1] 的調整幅度為 dw[1]
dw[2] = rate * x[2] * e; w[2] += dw[2]; // w[2] 的調整幅度為 dw[2]
if (loop % 10 == 0)
log("%d:x=(%s,%s,%s) w=(%s,%s,%s) y=%s yd=%s e=%s", loop,
x[0].toFixed(3), x[1].toFixed(3), x[2].toFixed(3),
w[0].toFixed(3), w[1].toFixed(3), w[2].toFixed(3),
y.toFixed(3), yd.toFixed(3), e.toFixed(3));
}
if (Math.abs(eSum) < 0.0001) return w; // 當訓練結果誤差夠小時,就完成訓練了。
}
return null; // 否則,就傳會 null 代表訓練失敗。
}
}
function learn(tableName, truthTable) { // 學習主程式:輸入為目標真值表 truthTable 與其名稱 tableName。
log("================== 學習 %s 函數 ====================", tableName);
var p = new Perceptron(); // 建立感知器物件
var w = p.training(truthTable); // 訓練感知器
if (w != null) // 顯示訓練結果
log("學習成功 !");
else
log("學習失敗 !");
log("w=%j", w);
}
var andTable = [ [ 0, 0, 0 ], [ 0, 1, 0 ], [ 1, 0, 0 ], [ 1, 1, 1 ] ]; // AND 函數的真值表
var orTable = [ [ 0, 0, 0 ], [ 0, 1, 1 ], [ 1, 0, 1 ], [ 1, 1, 1 ] ]; // OR 函數的真值表
var xorTable = [ [ 0, 0, 0 ], [ 0, 1, 1 ], [ 1, 0, 1 ], [ 1, 1, 0 ] ]; // XOR 函數的真值表
learn("and", andTable); // 學習 AND 函數
learn("or", orTable); // 學習 OR 函數
learn("xor", xorTable); // 學習 XOR 函數執行結果
D:\Dropbox\Public\web\ai\code>node perceptron.js
================== 學習 and 函數 ====================
0:x=(-1.000,0.000,0.000) w=(1.000,0.000,0.000) y=0.000 yd=0.000 e=0.000
0:x=(-1.000,0.000,1.000) w=(1.000,0.000,0.000) y=0.000 yd=0.000 e=0.000
0:x=(-1.000,1.000,0.000) w=(1.000,0.000,0.000) y=0.000 yd=0.000 e=0.000
0:x=(-1.000,1.000,1.000) w=(0.990,0.010,0.010) y=0.000 yd=1.000 e=1.000
10:x=(-1.000,0.000,0.000) w=(0.900,0.100,0.100) y=0.000 yd=0.000 e=0.000
10:x=(-1.000,0.000,1.000) w=(0.900,0.100,0.100) y=0.000 yd=0.000 e=0.000
10:x=(-1.000,1.000,0.000) w=(0.900,0.100,0.100) y=0.000 yd=0.000 e=0.000
10:x=(-1.000,1.000,1.000) w=(0.890,0.110,0.110) y=0.000 yd=1.000 e=1.000
20:x=(-1.000,0.000,0.000) w=(0.800,0.200,0.200) y=0.000 yd=0.000 e=0.000
20:x=(-1.000,0.000,1.000) w=(0.800,0.200,0.200) y=0.000 yd=0.000 e=0.000
20:x=(-1.000,1.000,0.000) w=(0.800,0.200,0.200) y=0.000 yd=0.000 e=0.000
20:x=(-1.000,1.000,1.000) w=(0.790,0.210,0.210) y=0.000 yd=1.000 e=1.000
30:x=(-1.000,0.000,0.000) w=(0.700,0.300,0.300) y=0.000 yd=0.000 e=0.000
30:x=(-1.000,0.000,1.000) w=(0.700,0.300,0.300) y=0.000 yd=0.000 e=0.000
30:x=(-1.000,1.000,0.000) w=(0.700,0.300,0.300) y=0.000 yd=0.000 e=0.000
30:x=(-1.000,1.000,1.000) w=(0.690,0.310,0.310) y=0.000 yd=1.000 e=1.000
學習成功 !
w=[0.6599999999999997,0.34000000000000014,0.34000000000000014]
================== 學習 or 函數 ====================
0:x=(-1.000,0.000,0.000) w=(1.000,0.000,0.000) y=0.000 yd=0.000 e=0.000
0:x=(-1.000,0.000,1.000) w=(0.990,0.000,0.010) y=0.000 yd=1.000 e=1.000
0:x=(-1.000,1.000,0.000) w=(0.980,0.010,0.010) y=0.000 yd=1.000 e=1.000
0:x=(-1.000,1.000,1.000) w=(0.970,0.020,0.020) y=0.000 yd=1.000 e=1.000
10:x=(-1.000,0.000,0.000) w=(0.700,0.200,0.200) y=0.000 yd=0.000 e=0.000
10:x=(-1.000,0.000,1.000) w=(0.690,0.200,0.210) y=0.000 yd=1.000 e=1.000
10:x=(-1.000,1.000,0.000) w=(0.680,0.210,0.210) y=0.000 yd=1.000 e=1.000
10:x=(-1.000,1.000,1.000) w=(0.670,0.220,0.220) y=0.000 yd=1.000 e=1.000
20:x=(-1.000,0.000,0.000) w=(0.460,0.340,0.340) y=0.000 yd=0.000 e=0.000
20:x=(-1.000,0.000,1.000) w=(0.450,0.340,0.350) y=0.000 yd=1.000 e=1.000
20:x=(-1.000,1.000,0.000) w=(0.440,0.350,0.350) y=0.000 yd=1.000 e=1.000
20:x=(-1.000,1.000,1.000) w=(0.440,0.350,0.350) y=1.000 yd=1.000 e=0.000
學習成功 !
w=[0.37999999999999945,0.38000000000000017,0.38000000000000017]
================== 學習 xor 函數 ====================
0:x=(-1.000,0.000,0.000) w=(1.000,0.000,0.000) y=0.000 yd=0.000 e=0.000
0:x=(-1.000,0.000,1.000) w=(0.990,0.000,0.010) y=0.000 yd=1.000 e=1.000
0:x=(-1.000,1.000,0.000) w=(0.980,0.010,0.010) y=0.000 yd=1.000 e=1.000
0:x=(-1.000,1.000,1.000) w=(0.980,0.010,0.010) y=0.000 yd=0.000 e=0.000
10:x=(-1.000,0.000,0.000) w=(0.800,0.100,0.100) y=0.000 yd=0.000 e=0.000
10:x=(-1.000,0.000,1.000) w=(0.790,0.100,0.110) y=0.000 yd=1.000 e=1.000
10:x=(-1.000,1.000,0.000) w=(0.780,0.110,0.110) y=0.000 yd=1.000 e=1.000
10:x=(-1.000,1.000,1.000) w=(0.780,0.110,0.110) y=0.000 yd=0.000 e=0.000
...
900:x=(-1.000,0.000,0.000) w=(0.010,-0.010,-0.000) y=1.000 yd=0.000 e=-1.000
900:x=(-1.000,0.000,1.000) w=(-0.000,-0.010,0.010) y=0.000 yd=1.000 e=1.000
900:x=(-1.000,1.000,0.000) w=(-0.010,-0.000,0.010) y=0.000 yd=1.000 e=1.000
900:x=(-1.000,1.000,1.000) w=(-0.000,-0.010,-0.000) y=1.000 yd=0.000 e=-1.000
...
990:x=(-1.000,0.000,0.000) w=(0.010,-0.010,-0.000) y=1.000 yd=0.000 e=-1.000
990:x=(-1.000,0.000,1.000) w=(-0.000,-0.010,0.010) y=0.000 yd=1.000 e=1.000
990:x=(-1.000,1.000,0.000) w=(-0.010,-0.000,0.010) y=0.000 yd=1.000 e=1.000
990:x=(-1.000,1.000,1.000) w=(-0.000,-0.010,-0.000) y=1.000 yd=0.000 e=-1.000
學習失敗 !
w=null分析
您可以看到在上述執行結果中, AND 與 OR 兩個真值表,輸入到單層感知器進行訓練之後,都可以正確的進行學習,也就是單層感知器的輸出可以與該真值表完全一致,這代表單層感知器學習成功了。
但是對於 XOR 這個真值表,單層感知器卻無法讓輸出與真值表完全一致,這也正是 Minsky 所說的,單層感知器無法正確學習 XOR 函數的原因。
會產生這個現象的原因,可以用線性代數的概念解釋,下圖顯示了 AND, OR, XOR 等這三個真值表在二維線性空間的狀況,其中的粉紅色圓圈代表真值表的目標輸出值為 1,而淺藍色圓圈代表目標輸出為 0。
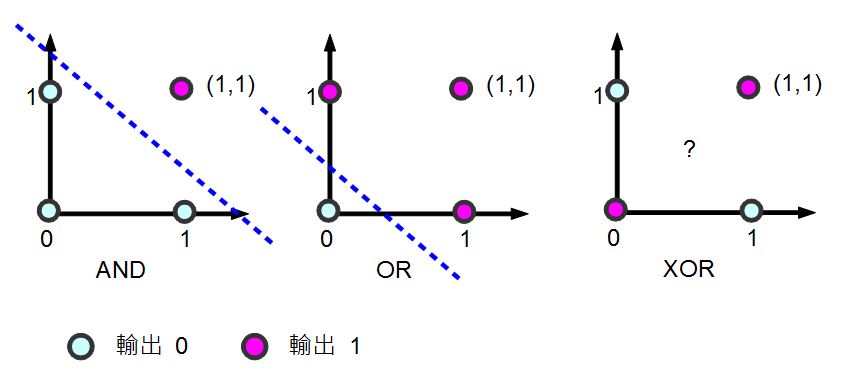
圖、單層感知器為何不能學習 XOR 函數的分析
您可以看到對於 AND 與 OR 都可以用一條線將「粉紅色圓圈」與「淺藍色圓圈」分割開來。但是對 XOR 而言,由於粉紅色與淺藍色分別處於斜對角,我們沒有辦法畫出單一條線將兩者分開,這也是會何上述單層感知器在學習 XOR 這個函數上會失敗的原因了。
結語
可惜的是,單層感知器並沒有辦法學會任意的布林函數,這個結果雖然令人失望,但是期望這麼簡單的模型就能擁有強大的能力,其實是一種非常天真的想法。
不過、如果我們將這種單層的網路繼續擴充,變成雙層以上的網路的話,其能力就會大大的提升了,這也就是我們接下來要探討的主題,反傳遞演算法 (Back-Propagation Algorithm) 了。
參考文獻
【本文由陳鍾誠取材並修改自 維基百科,採用創作共用的 姓名標示、相同方式分享 授權】
多層感知器與反傳遞演算法實作 - 使用 JavaScript+Node.js
前言
在前一篇文章中,我們討論了「單層感知器」的實作方式,然而單層感知器並沒有辦法處理像 XOR 這樣的函數。
為了提升「感知器」的能力,我們可以在輸入與輸出節點之間,再加入一些隱藏層,並透過這些隱藏層對整個學習空間進行更多次的分割,以便能處理 XOR 這類難以用單一線性函數分割的問題。
但是加入了隱藏層之後,感知器的學習與訓練就更為複雜了,這時必須有足夠的「數學理論」才能為「多層感知器」提供一個方向,而「反傳遞演算法」 (Back-Propagation) 正是這樣一個可以提供「多層感知器」學習方向的好東西,其數學基礎則是建構在多變數微分「梯度」概念之上的一種「梯度下降法」。
事實上、反傳遞演算法 (Back-Propagation) 的概念在 1974 年就由 Paul J. Werbos 所提出來了,但沒有受到重視,後來在 1986 年又被 Rumelhart 重新發明了出來,而且受到了廣泛的重視。
在本文中,我們將說明「多層感知器」與「反傳遞演算法」的概念,並用 Node.js+JavaScript 進行實作。
模型與數學原理
以下是本文程式所採用的一個「多層感知器」模型,其中包含「輸入層、隱藏層與輸出層」,這種多層感知器與上一篇「單層感知器」的一個明顯不同點,在於擁有一個隱藏層,因此其能力增強了很多。

圖、多層感知器模型 (本圖含一個隱藏層)
既然反傳遞演算法是一種梯度下降法,那麼我們只要能計算出梯度的方向,就能讓「多層感知器」的權重朝著能量下降最快的方向前進。
但是、梯度要怎麼計算呢?先讓我們來看一張多變數的能量曲線圖。
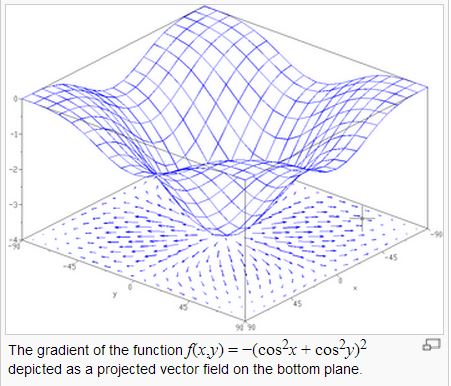
圖、曲面與每一點的梯度向量
在上圖中,底下的平面上所畫的向量,就是上面那個曲面在該點梯度的投影,指示了該平面最陡的下降方向。
在直覺概念上,曲面上某一點的梯度,其實是曲面在該點切平面的法向量,梯度的計算公式如下:
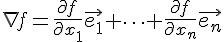
如果我們可以計算某函數之梯度的話,只要朝著梯度的方向走去,就是最快下降的道路了。
採用這種沿著梯度方向往下走的方法,就稱為「梯度下降法」(Gradient Descent),這種方法可以說是一種「貪婪演算法」(Greedy Algorithm),因為它每次都朝著最斜的方向走去,企圖得到最大的下降幅度。
為了要計算梯度,我們不能採用「單層感知器裏的那種不可微分的 sign() 步階函數」 (如下圖 a 所示),因為這樣就不能用微積分的方式計算出梯度了,而必須改用可以微分的連續函數 sigmoid() (如下圖 b 所示),這樣才能夠透過微分計算出梯度。
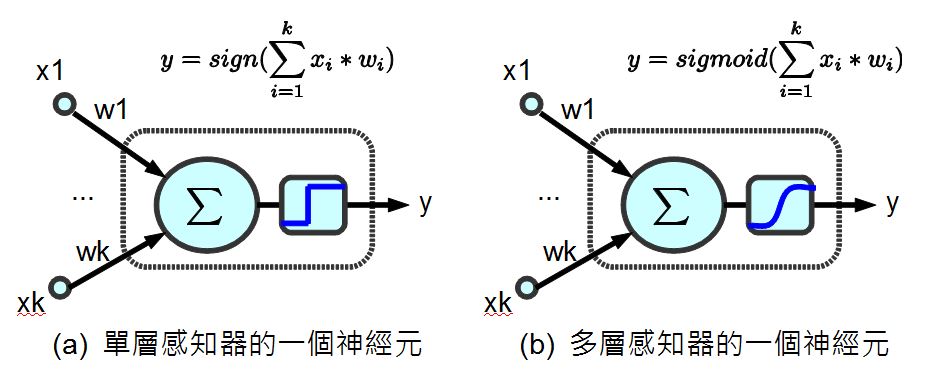
圖、兩種神經元之比較
當我們改成可微分的 sigmoid() 函數之後,就可以運用微積分公式,事先求出其微分函數 dsigmoid() 。舉例而言、在本文的程式中,我們就用了雙曲正切函數 tanh(x) 作為 sigmoid() 函數,其定義如下所示:
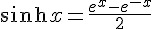
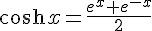
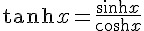
由於 tanh(x) 的微分是 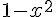 ,因此在下列這段程式中,我們定義了這些函數的計算方式。
,因此在下列這段程式中,我們定義了這些函數的計算方式。
var tanh=function(x) {
return (Math.exp(x) - Math.exp(-x)) / (Math.exp(x) + Math.exp(-x));
}
function sigmoid(x) {
return tanh(x); // 表現較好
}
function dsigmoid(x) {
return 1.0 - x*x;
}上述程式中 dsigmoid(y) 中的 1.0 - x*x 則是 y=tanh(x) 的微分式,對每個 y=tanh(x) 都取微分式的時候,其實就是梯度的方向。
(筆者註:有些實作會採用 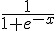 作為 sigmoid() 函數,這與 tanh(x) 函數的形狀非常類似,也是一種可行的方法)。
作為 sigmoid() 函數,這與 tanh(x) 函數的形狀非常類似,也是一種可行的方法)。
程式碼
檔案:backprop.js
// Back-Propagation Neural Networks (JavaScript 版)
// 由陳鍾誠修改自 Neil Schemenauer 的 Python 版
// Python 程式網址為: http://arctrix.com/nas/python/bpnn.py
var log = console.log;
// 建立大小為 n 的陣列並填入初始值 fill
var makeArray=function(n, fill) {
var a = [];
for (var i=0; i<n; i++)
a.push(fill);
return a;
}
// 建立大小為 I*J 的矩陣並填入初始值 fill
var makeMatrix=function(I, J, fill) {
var m = [];
for (var i=0; i<I; i++)
m.push(makeArray(J, fill));
return m;
}
// numbersToStr():以精確度為 precision 個小數來輸出陣列 array
var numbersToStr=function(array, precision) {
var rzStr = "";
for (var i=0; i<array.length; i++) {
if (array[i]>=0)
rzStr+=" "+array[i].toFixed(precision)+" ";
else
rzStr+=array[i].toFixed(precision)+" ";
}
return rzStr;
}
// rand():取得 a 到 b 之間的一個隨機亂數
var rand=function(a, b) {
return (b-a)*Math.random() + a;
}
// sigmoid(x)=tanh(x)
function sigmoid(x) {
var tanh = (Math.exp(x) - Math.exp(-x)) / (Math.exp(x) + Math.exp(-x));
return tanh; // 雙曲正切函數
}
// dsigmoid(x)=1-x^2;
// 參考:http://pynopticon.googlecode.com/svn/trunk/src/vlfeat/toolbox/special/dsigmoid.m
// 參考:http://en.wikipedia.org/wiki/Sigmoid_function
function dsigmoid(x) {
return 1.0 - x*x;
}
function NeuralNet() {
// init():設定網路結構與權重的隨機初始值的函數。
this.init=function(ni, nh, no) {
// number of input, hidden, and output nodes
this.ni = ni + 1; // +1 for bias node
this.nh = nh;
this.no = no;
// activations for nodes : 建立各層的節點陣列
this.ai = makeArray(this.ni, 1.0);
this.ah = makeArray(this.nh, 1.0);
this.ao = makeArray(this.no, 1.0);
// create weights : 建立權重矩陣
this.wi = makeMatrix(this.ni, this.nh, 0.0);
this.wo = makeMatrix(this.nh, this.no, 0.0);
// set them to random vaules : 隨機設定權重初始值。
for (var i=0; i<this.ni; i++)
for (var j=0; j<this.nh; j++)
this.wi[i][j] = rand(-0.2, 0.2);
for (var j=0; j<this.nh; j++)
for (var k=0; k<this.no; k++)
this.wo[j][k] = rand(-2.0, 2.0);
// last change in weights for momentum : 上一次的改變量矩陣,用來當動量以便爬過肩型區域。
this.ci = makeMatrix(this.ni, this.nh, 0.0);
this.co = makeMatrix(this.nh, this.no, 0.0);
return this;
}
// update() : 計算網路的輸出的函數
this.update=function(inputs) {
// input activations : 設定輸入值
for (var i=0; i<this.ni-1; i++)
this.ai[i] = inputs[i];
// hidden activations : 計算隱藏層輸出值 ah[j]
for (var j=0; j<this.nh; j++) {
var sum = 0.0;
for (var i=0; i<this.ni; i++)
sum = sum + this.ai[i] * this.wi[i][j];
this.ah[j] = sigmoid(sum);
}
// output activations : 計算輸出層輸出值 ao[k]
for (var k=0; k<this.no; k++) {
var sum = 0.0;
for (var j=0; j<this.nh; j++)
sum = sum + this.ah[j] * this.wo[j][k];
this.ao[k] = sigmoid(sum);
}
return this.ao; // 傳回輸出層輸出值 ao
}
// backPropagate():反傳遞學習的函數 (重要)
this.backPropagate = function(targets, rate, moment) {
// calculate error terms for output : 計算輸出層誤差
var output_deltas = makeArray(this.no, 0.0);
for (var k=0; k<this.no; k++) {
var error = targets[k]-this.ao[k];
output_deltas[k] = dsigmoid(this.ao[k]) * error;
}
// calculate error terms for hidden : 計算隱藏層誤差
var hidden_deltas = makeArray(this.nh, 0.0);
for (var j=0; j<this.nh; j++) {
var error = 0.0;
for (var k=0; k<this.no; k++) {
// 注意、在此輸出層誤差 output_deltas 會反傳遞到隱藏層,因此才稱為反傳遞演算法。
error = error + output_deltas[k]*this.wo[j][k];
}
hidden_deltas[j] = dsigmoid(this.ah[j]) * error;
}
// update output weights : 更新輸出層權重
for (var j=0; j<this.nh; j++) {
for (var k=0; k<this.no; k++) {
var change = output_deltas[k]*this.ah[j];
this.wo[j][k] = this.wo[j][k] + rate*change + moment*this.co[j][k];
this.co[j][k] = change;
// print N*change, M*this.co[j][k]
}
}
// update input weights : 更新輸入層權重
for (var i=0; i<this.ni; i++) {
for (var j=0; j<this.nh; j++) {
var change = hidden_deltas[j]*this.ai[i];
this.wi[i][j] = this.wi[i][j] + rate*change + moment*this.ci[i][j];
this.ci[i][j] = change;
}
}
// calculate error : 計算輸出層誤差總合
var error = 0.0;
for (var k=0; k<targets.length; k++)
error = error + 0.5*Math.pow(targets[k]-this.ao[k],2);
return error;
}
// test() : 對真值表 (訓練樣本) 中的每個輸入都印出「網路輸出」與「期望輸出」,以便觀察學習結果是否都正確。
this.test = function(patterns) {
for (var p in patterns) {
var inputs = patterns[p][0];
var outputs= patterns[p][1];
log("%j -> [%s] [%s]", inputs, numbersToStr(this.update(inputs), 0), numbersToStr(outputs, 0));
// this.dump();
}
}
// train(): 主要學習函數,反覆呼叫反傳遞算法
// 參數:rate: learning rate (學習速率), moment: momentum factor (動量常數)
this.train=function(patterns, iterations, rate, moment) {
for (var i=0; i<iterations; i++) {
var error = 0.0;
for (var p in patterns) {
var pat=patterns[p];
var inputs = pat[0];
var targets = pat[1];
var outputs = this.update(inputs);
error = error + this.backPropagate(targets, rate, moment);
}
if (i % 100 == 0)
log('%d:error %j', i, error);
}
}
}
module.exports = NeuralNet; // 匯出 NeuralNet 物件。執行範例 1 : 學習 XOR 函數
檔案:backprop_xor.js
var NN = require("./backprop");
pat = [
[[0,0], [0]],
[[0,1], [1]],
[[1,0], [1]],
[[1,1], [0]]
];
// create a network with two input, two hidden, and one output nodes
nn = new NN().init(2, 2, 1);
// train it with some patterns
nn.train(pat, 1000, 0.5, 0.1);
// test it
nn.test(pat);執行結果:
D:\Dropbox\Public\web\ai\code\neural>node backprop_xor
0:error 1.1411586806597014
100:error 0.15669092345306487
200:error 0.0044566959936791035
300:error 0.0018489705409186357
400:error 0.0011477205633429219
500:error 0.0008277968129286529
600:error 0.0006456614467953627
700:error 0.005231441443909679
800:error 0.0004595906757934737
900:error 0.0003945408066808508
[0,0] -> [ 0 ] [ 0 ]
[0,1] -> [ 1 ] [ 1 ]
[1,0] -> [ 1 ] [ 1 ]
[1,1] -> [-0 ] [ 0 ]執行範例 2 : 學習七段顯示器函數
檔案:backprop_7seg.js
/* 七段顯示器排列圖示
A
F B
G
E C
D
*/
var NN = require("./backprop");
pat = [
// A B C D E F G
[[1,1,1,1,1,1,0], [0,0,0,0]], // 0
[[0,1,1,0,0,0,0], [0,0,0,1]], // 1
[[1,1,0,1,1,0,1], [0,0,1,0]], // 2
[[1,1,1,1,0,0,1], [0,0,1,1]], // 3
[[0,1,1,0,0,1,1], [0,1,0,0]], // 4
[[1,0,1,1,0,1,1], [0,1,0,1]], // 5
[[1,0,1,1,1,1,1], [0,1,1,0]], // 6
[[1,1,1,0,0,0,0], [0,1,1,1]], // 7
[[1,1,1,1,1,1,1], [1,0,0,0]], // 8
[[1,1,1,1,0,1,1], [1,0,0,1]] // 9
];
// create a network with 7 input, 5 hidden, and 4 output nodes
nn = new NN().init(7, 5, 4);
// train it with some patterns
nn.train(pat, 10000, 0.2, 0.01);
// test it
nn.test(pat);執行結果:
D:\Dropbox\Public\web\ai\code\neural>node backprop_7seg
0:error 21.80370718175807
100:error 3.0996784544877736
200:error 2.9554663137424373
300:error 2.9322332121195545
400:error 0.9175505320368402
500:error 0.5911840202045504
600:error 0.6702566860375645
700:error 0.6175745429758741
800:error 0.6073471516556047
900:error 0.601200049561361
1000:error 0.5810463514787689
1100:error 0.5364677212922591
1200:error 0.532025286869445
1300:error 0.46666848524996085
1400:error 0.48129628693742754
1500:error 0.8155362088747744
1600:error 0.5829386518767099
1700:error 0.6944742612114545
1800:error 0.49717362214697597
1900:error 0.40957109669176334
2000:error 0.5388564563993076
2100:error 0.3703582901903478
2200:error 0.5178647638260341
2300:error 0.1764373289120007
2400:error 0.25347246319196093
2500:error 0.33310966813566406
2600:error 0.17106878914718923
2700:error 0.1365002209754472
2800:error 0.1594051132697459
2900:error 0.3070991793860354
3000:error 0.3766039636947747
3100:error 0.3555367190225767
3200:error 0.11555541960454409
3300:error 0.11367500949340971
3400:error 0.12234128181753154
3500:error 0.1675446667610037
3600:error 0.09044262748000728
3700:error 0.08628776394501735
3800:error 0.27906234926518514
3900:error 0.04818459875532369
4000:error 0.062418918530088664
4100:error 0.2804289611800696
4200:error 0.13725495522690973
4300:error 0.12719742994691247
4400:error 0.07177660395615833
4500:error 0.08548411758763816
4600:error 0.03974217740792855
4700:error 0.09595126476746213
4800:error 0.03853494372617759
4900:error 0.06360901767700806
5000:error 0.07246959735102428
5100:error 0.05362418748287888
5200:error 0.04669033343340621
5300:error 0.03270696475959521
5400:error 0.03940008954106113
5500:error 0.047208537352753516
5600:error 0.049368429554604215
5700:error 0.042625347453785954
5800:error 0.056241589618292134
5900:error 0.016798400589135128
6000:error 0.03404851177897533
6100:error 0.028972975396903942
6200:error 0.01572555942490573
6300:error 0.048110746037786964
6400:error 0.039118552165591194
6500:error 0.03954060666366999
6600:error 0.047240563507126423
6700:error 0.013729342899560402
6800:error 0.03734015049471263
6900:error 0.04385222818693631
7000:error 0.038098235270263764
7100:error 0.014325393180305138
7200:error 0.039093361005808284
7300:error 0.011914229228792664
7400:error 0.012490068609142688
7500:error 0.010110888778014877
7600:error 0.017266400583083073
7700:error 0.037972260655506615
7800:error 0.010317947862704183
7900:error 0.02181165885044425
8000:error 0.033354842242808616
8100:error 0.033244707069915634
8200:error 0.02269772865101642
8300:error 0.008219315372175379
8400:error 0.03342460798252796
8500:error 0.008080093519395289
8600:error 0.02466937317542233
8700:error 0.03307092886686206
8800:error 0.033433889409569414
8900:error 0.031423007039930506
9000:error 0.018154152094468162
9100:error 0.008635680953338276
9200:error 0.030890671102892397
9300:error 0.009020762345545542
9400:error 0.015823853695083934
9500:error 0.029353956299920176
9600:error 0.03028116871034789
9700:error 0.03009059907189612
9800:error 0.025996249652393937
9900:error 0.009595759182954272
[1,1,1,1,1,1,0] -> [ 0 0 -0 -0 ] [ 0 0 0 0 ]
[0,1,1,0,0,0,0] -> [ 0 -0 -0 1 ] [ 0 0 0 1 ]
[1,1,0,1,1,0,1] -> [-0 -0 1 0 ] [ 0 0 1 0 ]
[1,1,1,1,0,0,1] -> [-0 0 1 1 ] [ 0 0 1 1 ]
[0,1,1,0,0,1,1] -> [ 0 1 -0 0 ] [ 0 1 0 0 ]
[1,0,1,1,0,1,1] -> [-0 1 -0 1 ] [ 0 1 0 1 ]
[1,0,1,1,1,1,1] -> [-0 1 1 0 ] [ 0 1 1 0 ]
[1,1,1,0,0,0,0] -> [-0 1 1 1 ] [ 0 1 1 1 ]
[1,1,1,1,1,1,1] -> [ 1 -0 -0 0 ] [ 1 0 0 0 ]
[1,1,1,1,0,1,1] -> [ 1 0 -0 1 ] [ 1 0 0 1 ]結語
您可以看到上述兩個訓練案例,都是完全正確的,這代表反傳遞演算法可以讓多層感知器學會 XOR 與七段顯示器的函數。
當然、多層感知器也可以學會更難的問題,像是手寫的數字與英文字辨認等等,手寫中文辨認和語音辨認當然也是可行的,只不過需要很多的訓練範例與節點,學習的效果才會夠好就是了!
參考文獻
【本文由陳鍾誠取材並修改自 維基百科,採用創作共用的 姓名標示、相同方式分享 授權】
類神經網路轉譯成 C++ (作者:張藝瀚)
我的第一支類神經網路程式終於誕生啦!
雖然只是轉譯自别人的 C# 程式範例,雖然只是簡單的 XOR Gate,依我的理解補上缺的程式碼, 第一次執行成功看到輸出值逐漸收歛, 感覺很有成就感, 總算實現了多年的心願! 後續目標是做出更複雜的模型 (好歹要有反饋式), 做成 Multithread, 做到雲端...
感謝 C#.Net 版的原作者漠哥, 同意我轉譯成 C++ 使用, 原作網址是:
轉譯好, 確定可以在 Linux 下編譯執行的C++程式碼分享如下:
/* =========================================================================
Summary :
類神經網路 - 學習機器人
Compiler :
linux:
g++ -lrt -o ./Neural3 ./Neural3.cpp
Usage :
./Neural3
Reference :
類神經網路-神經網路物件 @ 人生四十宅開始二號宅 痞客邦 PIXNET
http://mogerwu.pixnet.net/blog/post/25518602
Remark :
History :
yyyy.mm.dd Author Discription
---------- ---------------- ---------------------------------------------
2010.11.10 Yihhann Chang Translate from the C# source code of Moger Wu
---------- ---------------- ---------------------------------------------
Test:
./Neural3
========================================================================= */
#include <ctype.h>
#include <math.h> // for exp(), fabs(), sqrt()
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h> // for srand()
// 之前寫的類神經程式因為考慮到多執行緒,許多人看不懂,這一篇使用陣列來表達
// 神經元,並且完全不考慮多執行緒的問題,應該比較容易理解。
// 首先當然就是設計神經元,Value為神經元輸出值,如果神經元位於輸入層,它
// 同時也是輸入值,這樣設計是為了後面計算的程式好寫。神經元初始化的時候
// 必須要告訴他上一層的神經元個數,這樣他才能準備好神經鍵陣列Synapse。初
// 始化的時候讓閥值(GateValue)、神經鍵(Synapse)都使用亂數設定初始值,
// 根據經驗如果使用固定值,也就是1與-1交錯的初始值,在某些案例中可能不容
// 易收斂。
//
// 同時神經元也包含誤差值(diffentValue)、閥值修正(fixGateValue)、神經鍵
// 修正(fixSynapse[]),這樣把所有的值都放一起應該比較容易懂了吧。
class Element
{
public :
double Value;
double GateValue;
double *Synapse;
// internal :
double diffentValue;
double fixGateValue;
double *fixSynapse;
int UpperLayerSize; // the length of Synapse and fixSynapse
public :
Element(int upperLayerSize) {
int s;
UpperLayerSize = upperLayerSize;
Synapse = new double[UpperLayerSize];
fixSynapse = new double[UpperLayerSize];
if (UpperLayerSize > 0) {
GateValue = ( (double)rand() / RAND_MAX ) * 2 - 1;
for ( s = 0; s < UpperLayerSize; s++) {
Synapse[s] = ( (double)rand() / RAND_MAX ) * 2 - 1;
}
}
}
// 解構式, 釋放動態配置的資源
~Element() {
if( Synapse != NULL ) delete Synapse;
if( fixSynapse != NULL ) delete fixSynapse;
}
};
// end of class Element
// 接著解釋網路元件的設計。
// Element ***Elements;
// 用一個二維的動態陣列來儲存神經元,陣列第一個註腳就是神經層,第二個註腳
// 就是每個神經層的神經元。
const int ELEMENTS_LENGTH = 3; // Network::Elements.length, 三種 Layer
class Network {
public:
Element ***Elements;
double *Standar;
double DiffentValue;
// Elements[?].length, 三種 Layer 的元素數, 方便跑迴圈用
int Elements_lengths[ELEMENTS_LENGTH];
// 為了程式方便,設計兩個屬性,直接傳回輸入層和輸出層。
Element ** OutputLayer; // Elements[2];
Element ** InputLayer; // Elements[0];
Network(int InputLayerSize, int HiddenLayerSize, int OutputLayerSize) {
// 使用動態的方式宣告每一層的大小,這樣也比較符合實際網路架構。
Elements = new Element **[3];
Elements[0] = new Element *[InputLayerSize];
Elements[1] = new Element *[HiddenLayerSize];
Elements[2] = new Element *[OutputLayerSize];
OutputLayer = Elements[2];
InputLayer = Elements[0];
Elements_lengths[0] = InputLayerSize;
Elements_lengths[1] = HiddenLayerSize;
Elements_lengths[2] = OutputLayerSize;
Standar = new double[OutputLayerSize];
int upperLayerSize = 0;
for (int l = 0; l < ELEMENTS_LENGTH; l++) {
for (int e = 0; e < Elements_lengths[l]; e++) {
Elements[l][e] = new Element(upperLayerSize);
}
upperLayerSize = Elements_lengths[l];
}
}
// end of Network(int InputLayerSize, int HiddenLayerSize, int OutputLayerSize)
// 解構式, 釋放動態配置的資源
~Network() {
if( Elements != NULL ) {
for (int l = 0; l < ELEMENTS_LENGTH; l++) {
if( Elements[l] != NULL ) {
for (int e = 0; e < Elements_lengths[l]; e++) {
if( Elements[l][e] != NULL ) delete Elements[l][e];
}
delete Elements[l];
}
}
delete Elements;
}
if( Standar != NULL ) delete Standar;
}
// end of ~Network()
// 因為網路的修正動作是將所有的範例都計算過修正值之後,再一次進行修正,並
// 且再用新的網路進行計算,因此必須在計算之前將網路的動態值歸零,也就是說
// 下面這段程式裏面所歸零的值都是加總的值,必須在新的週期開始的時候清除掉。
void ClearValue() {
DiffentValue = 0;
for (int l = 0; l < ELEMENTS_LENGTH; l++) {
for (int e = 0; e < Elements_lengths[l]; e++) {
Elements[l][e]->Value = 0;
Elements[l][e]->diffentValue = 0;
Elements[l][e]->fixGateValue = 0;
for (int s = 0; s < Elements[l][e]->UpperLayerSize; s++) {
Elements[l][e]->fixSynapse[s] = 0;
}
}
}
// ==== DEBUG ==== TODO : LastHidden 不曉得是哪來的, 後面也沒用到
// for (int h = 0; h < LastHidden.Length; h++) {
// LastHidden[h] = 0;
// }
}
// 計算網路的輸出值,看過書的應該可以看得懂,數學公式實在不好貼,等我想到
// 好方法再補上吧。
void Summation() {
for (int l = 1; l < ELEMENTS_LENGTH; l++) {
for (int e = 0; e < Elements_lengths[l]; e++) {
double outvalue = -Elements[l][e]->GateValue;
for (int s = 0; s < Elements[l][e]->UpperLayerSize; s++) {
outvalue += Elements[l - 1][s]->Value *
Elements[l][e]->Synapse[s];
}
Elements[l][e]->Value = (double)(1 / (1 + exp(-outvalue)));
}
}
}
// 計算網路誤差值,這裡我把公式分成兩種,一種是用來計算修正網路值用的,
// 使用書上所寫的公式。而另一個是給人看的,同時也是輸出值夠精密到可以跳
// 出的依據。為甚麼要這麼做請參考這一篇,雖然很多人來看,還是沒有人告訴
// 我答案,所以我用土方法解決這個問題。
void CalcDiffent() {
//output layer
for (int e = 0; e < Elements_lengths[2]; e++) {
//給電腦看的用標準差公式
OutputLayer[e]->diffentValue =
(Standar[e] - OutputLayer[e]->Value) *
(OutputLayer[e]->Value * (1 - OutputLayer[e]->Value) + 0.01);
//給人看的用傳統公式
DiffentValue += fabs(Standar[e] - OutputLayer[e]->Value);
}
//hidden layer
for (int l = ELEMENTS_LENGTH - 2; l > 0; l--) {
for (int e = 0; e < Elements_lengths[l]; e++) {
double sumDiff = 0;
for (int ne = 0; ne < Elements_lengths[l + 1]; ne++) {
sumDiff += Elements[l + 1][ne]->Synapse[e] *
Elements[l + 1][ne]->diffentValue;
}
Elements[l][e]->diffentValue = (Elements[l][e]->Value *
(1 - Elements[l][e]->Value)) * sumDiff;
}
}
}
// 得到誤差值之後就可以依照誤差值來得到修正值,因為要所有的範例都學習過
// 才進行網路修正,所以所有的修正都是累加的。公式還是請自行參考書上說明
// 。事實上這一段程式可以跟計算誤差值的程式合併,分開來寫比較容易看得懂
// ,如果想要效能好一點就請將它合併在一起。
void CalcFixValue(double LearnSpeed) {
for (int l = ELEMENTS_LENGTH - 1; l > 0; l--) {
for (int e = 0; e < Elements_lengths[l]; e++) {
Elements[l][e]->fixGateValue =
-LearnSpeed * Elements[l][e]->diffentValue;
for (int ue = 0; ue < Elements_lengths[l - 1]; ue++) {
Elements[l][e]->fixSynapse[ue] +=
LearnSpeed * Elements[l][e]->diffentValue *
Elements[l - 1][ue]->Value;
}
}
}
}
// 當所有的範例都學習完成之後,當然就是要實際修正網路內容,修正值取平均,
// 所以需要傳入範例個數來進行運算。
void FixNetwork(int SampleCount) {
for (int l = 1; l < ELEMENTS_LENGTH; l++) {
for (int e = 0; e < Elements_lengths[l]; e++) {
Elements[l][e]->GateValue +=
Elements[l][e]->fixGateValue / sqrt((double)SampleCount);
for (int s = 0; s < Elements[l][e]->UpperLayerSize; s++) {
Elements[l][e]->Synapse[s] +=
Elements[l][e]->fixSynapse[s] /
sqrt((double)SampleCount);
}
}
}
}
};
// end of class Network
// 學習機器人基礎類別
// 這個類是個基礎類,因為載入資料和將資料放進輸入層的動作,每一個案例都
// 不相同,因此使用必須繼承的關鍵字abstract宣告這個類別,並且宣告兩個方
// 法LoadSample和LoadData為必須實做的。
class RobotBase {
public :
int SampleCount;
// internal :
int inputLayerSize, outputLayerSize;
Network *worknet;
int noBestCount;
int learnSamples;
double bestDiffent; // = 10000;
// 建構式 ,賦與初值
RobotBase(){
bestDiffent = 10000;
worknet = NULL;
}
// 解構式, 釋放動態配置的資源
~RobotBase(){
if( worknet != NULL ) delete worknet;
}
// 純虛擬函式, 由繼承者實作
virtual void LoadSample() = 0;
virtual void LoadData(int SampleNo) = 0;
// public delegate void OnCycleFinish(int CycleNo, double BestDiffent, double NewDiffent);
// public event OnCycleFinish EventCycleFinish;
// public delegate void OnBadLearning(int NoBestCount);
// public event OnBadLearning EventBadLearning;
// 最後就是最重要的學習過程了,基本程式和前面VB.Net的寫法一樣,就是用
// 【找不到最佳值的次數】或【達到預定的精密度】來決定學習是否完成。不
// 過有的時候誤差值調整的幅度很小,可能導致跑了幾十萬次都還出不來,可
// 以考慮再增加一個對cycle的限制。
virtual void Learning(double LearnSpeed, int HiddenLayerSize,
int NoBestLimit, double Precision)
{
worknet = new Network(inputLayerSize, HiddenLayerSize, outputLayerSize);
bestDiffent = 10000;
int cycle = 0;
noBestCount = 0;
while ((noBestCount < NoBestLimit) && (bestDiffent > Precision)) {
double newDiffent;
cycle++;
worknet->ClearValue();
for (int sampleNo = 0; sampleNo < learnSamples; sampleNo++) {
LoadData(sampleNo);
worknet->Summation();
worknet->CalcDiffent();
worknet->CalcFixValue(LearnSpeed);
// ==== DEBUG ====
int e;
printf( "Input:( " );
for( e = 0; e < worknet->Elements_lengths[0]; e++)
printf( "%+f ", worknet->InputLayer[e]->Value );
printf( "), Standard:( " );
for( e = 0; e < worknet->Elements_lengths[2]; e++)
printf( "%f ", worknet->Standar[e] );
printf( "), Output:( " );
for( e = 0; e < worknet->Elements_lengths[2]; e++)
printf( "%f ", worknet->OutputLayer[e]->Value );
printf( ")\n" );
}
newDiffent = worknet->DiffentValue / learnSamples;
if (newDiffent < bestDiffent) {
bestDiffent = newDiffent;
noBestCount = 0;
}
else {
noBestCount++;
}
// if (EventBadLearning != null) EventBadLearning(noBestCount);
worknet->FixNetwork(learnSamples);
// if (EventCycleFinish != null) EventCycleFinish(cycle, bestDiffent, newDiffent);
// ==== DEBUG ====
printf( "cycle=%d, noBestCount=%d, bestDiffent=%0.8f, newDiffent=%0.8f\n",
cycle, noBestCount, bestDiffent, newDiffent );
}
delete worknet;
worknet = NULL;
}
};
// end of class RobotBase
// XOR為範例
class RobotXOR : public RobotBase
{
public :
// XOR 學習機
RobotXOR() {
inputLayerSize = 2; // 輸入值 2 個
outputLayerSize = 1; // 輸出結果1 個
learnSamples = 4; // 輸入組合只有 4 種
}
// 設定輸入樣本, 及標準答案
void LoadData( int sampleNo )
{
switch ( sampleNo )
{
case 0:
worknet->InputLayer[0]->Value = -1;
worknet->InputLayer[1]->Value = -1;
worknet->Standar[0] = 0;
break;
case 1:
worknet->InputLayer[0]->Value = -1;
worknet->InputLayer[1]->Value = 1;
worknet->Standar[0] = 1;
break;
case 2:
worknet->InputLayer[0]->Value = 1;
worknet->InputLayer[1]->Value = -1;
worknet->Standar[0] = 1;
break;
case 3:
worknet->InputLayer[0]->Value = 1;
worknet->InputLayer[1]->Value = 1;
worknet->Standar[0] = 0;
break;
}
}
// end of void LoadData( int sampleNo )
// 這函數應該是用來取代 LoadData, 當樣本數量龐大時, 可以改從檔案/資料庫載入
void LoadSample()
{
}
// 通常隱藏層的寬度可以設置為
// hiddenLayerSize=(inputLayerSize+outputLayerSize)/2
// ,但是許多案例並不能滿足需求,而是要用嘗試錯誤法去求得合適的隱藏層寬度
// 。前面Learning宣告為可以被重新包裝的,就是?了這個,當然你也可以把它包
// 裝在一起。如果一個學習週期跳出後,精密度不夠就試著調整隱藏層寬度。
void Learning(double LearnSpeed, int HiddenLayerSize, int CycleLimit,
double Precision)
{
while (bestDiffent > Precision) {
// if (EventHiddenLayerChange != null) EventHiddenLayerChange(HiddenLayerSize);
this->RobotBase::Learning(LearnSpeed, HiddenLayerSize, CycleLimit,
Precision);
if (bestDiffent > Precision) {
HiddenLayerSize = (int)(HiddenLayerSize * 1.2 + 1);
}
// ==== DEBUG ====
printf( "bestDiffent=%0.8f, Precision=%0.8f, HiddenLayerSize=%d\n\n",
bestDiffent, Precision, HiddenLayerSize );
}
}
};
// end of class RobotXOR
// ===========================================================================
int main()
{
RobotXOR *Robot;
srand ( time(NULL) ); /* initialize random seed: */
printf( "Hello~\n" );
Robot = new RobotXOR;
Robot->Learning(
1000, // double LearnSpeed
10, // int HiddenLayerSize
10, // int CycleLimit
0.00001 // double Precision
);
delete Robot;
printf( "Bye~\n" );
}程式人文集
Arduino入門教學(16) – Amarino 的 SpeakToArduino 範例程式 (作者:Cooper Maa)
這篇是寫給 amarino 初學者看的,目的是教導你如何執行 Amarino 的 SpeakToArduino 範例程式。SpeakToArduino 這個範例示範如何用 Android 手機聲控 Arduino。
所需材料
- Android 手機一支
- Arduino x1
- bluetooth module x 1
- 紅色 LED, 綠色 LED 及藍色 LED 各一顆(若無特定顏色 LED,可用其它顏色的 LED 取代),或一顆 RGB Led
- 220 歐姆電阻 x 3
Step 1:安裝 Amarino
到 http://www.amarino-toolkit.net/ 下載下列 App 並安裝到 Android 手機上:
Step 2: 安裝 Arduino IDE 與 MeetAndroid Library
如果你電腦上還沒有 Arduino IDE,請先到 http://arduino.cc/en/Main/Software 下載軟體,下載後解壓縮即可。
接著下載 MeetAndroid Library,把 MeetAndroid 解到 Arduino IDE 安裝目錄下的 libraries 資料夾。
重新啟動 Arduino IDE,在 Sketch > Import Library 底下應該會看到 MeetAndroid,如下圖:
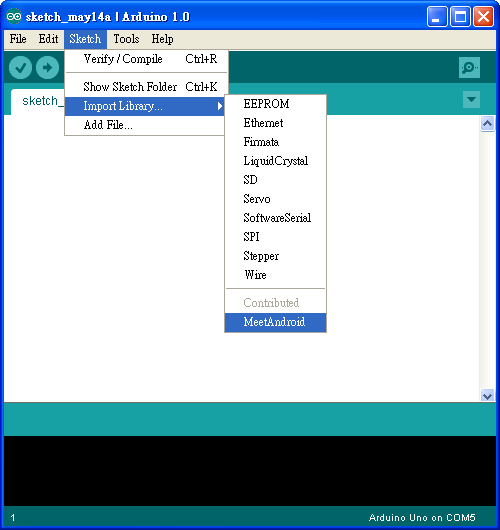
Step 3:連接 LED
參考下圖,把紅、綠、藍三顆 LED 分別接到 pin 9, 10, 11,LED 的接法為: 長腳(陽極)接到 pin 腳,而短腳(陰極)串接一顆 220 ohm 電阻接到 GND:
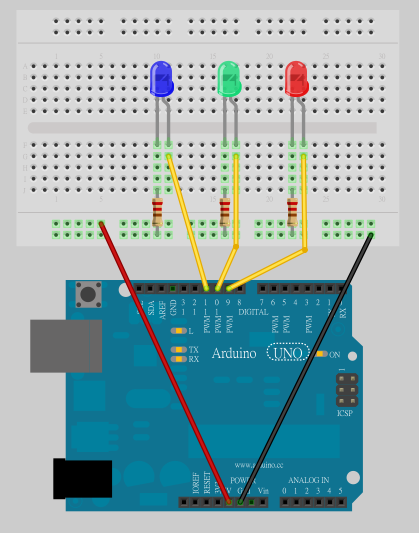
Step 4: 上傳 SpeakToArduino 程式
到這裏下載,並使用 Arduino IDE 打開 SpeakToArduino 程式。
程式所用的 baud rate 預設是 57600 bps,如果你的藍芽模組不是 57600 bps,請做適當的調整:
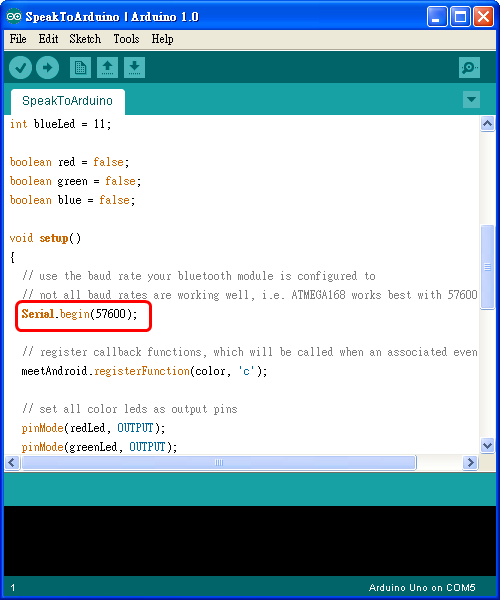
然後把程式上傳到 Arduino 板子上。
Step 5:連接藍芽模組
我用的是 廣州匯承信息科技 的 HC-0x 系列藍芽模組,下圖是 HC-0x 藍芽模組的外觀:

▲ HC-0x 藍芽模組 (圖左:正面圖,圖右:背面圖)
連接方法很簡單,照下表把 Arduino 和藍芽模組連接起來就好:
| Arduino | 藍芽模組 | 備註 |
|---|---|---|
| 5V | VCC | 注意電源不可接錯 |
| GND | GND | 注意電源不可接錯 |
| RXD | TXD | |
| TXD | RXD |

有兩點要注意:第一是電源千萬不可接錯,不然可能會燒壞藍芽模組,第二是 Arduino 的 RXD 要接藍芽模組的 TXD,而 Arduino 的 TXD 要接藍芽模組的 RXD。
通電之後,藍芽模組上的 LED 會一直閃爍:

Step 6:執行 SpeakToArduino App
首先,先利用 Amarino 搜尋藍芽設備,找到設備後,將藍芽設備的 MAC Address 抄起來(記得不要在 Amarino 設定任何 Event!):

打開 Android 手機上的 SpeakToArduino App,你會看到這樣的畫面:
選手機 Menu 鍵 Set BT Device Address,手機會跳出這個畫面,此時請輸入剛剛抄下來的 MAC Address,然後按下【Save】鈕:
按一下手機 Back 鍵退出 SpeakToArduino App,然後重新啟動 SpeakToArduino,這樣 App 才會用新的 Mac Adress 跟藍芽模組連線。
如果一切順利,Android 手機就會跟 Arduino 建立連線,並且呈現如下圖的畫面(注意手機上方的 Status bar,若有成功與 Arduino 連線,status bar 上會顯示 Active connection: … 的訊息):
按下【Click and order your color】鈕,手機會跳出語音辨識的畫面:
這時便可以說出想要的顏色,例如 red, green, blue, white, pink, orange, yellow, dark 或 off,這時候 Arduino 上三顆 LED 便會同步改變亮度。比如當我說 red,這時 Android 手機就會叫 Arduino 把紅色 LED 打開:
如果你有 RGB Led,可以用一顆 RGB Led 取代三顆 Led,這樣更可以呈現 LED 顏色變化的效果。
參考資料
【本文作者為馬萬圳,原文網址為: http://coopermaa2nd.blogspot.tw/2012/07/speaktoarduino.html ,由陳鍾誠編輯後納入本雜誌】
OpenNI 2 的錯誤處理 (作者: Heresy Ku )
在上一篇的 《OpenNI 2 基本程式範例》 裡,Heresy 基本上是先整理了一下,要使用 Visual Studio 來進行 OpenNI 2 的程式開發的話,要怎樣進專案的設定,另外也用一個最簡單的例子,來說明 OpenNI 2 的程式要怎麼寫。而這一篇,則是再繼續做補充,讓程式更完整。
在上一個範例裡面,Heresy 為了版面、以及簡化程式碼的關係,是假設程式執行都沒有問題,所以把所有錯誤的檢查都拿掉了。不過實際上,程式在執行的時候,其實都是應該要考慮到各種錯誤狀況的!而 OpenNI 2 也有提供一些簡單的介面,可以用來檢查程式執行時,有沒有錯誤。
首先,和 OpenNI 1.x 的時候,OpenNI 大部分的函式,都會回傳一個代表結果的值,讓開發者可以據此判斷該函式是否已正確執行;而在 OpenNI 2,這個回傳的結果,是一個叫做 openni::Status 的列舉型別。基本的使用狀況,大致上如下:
openni::Status eRes = openni::OpenNI::initialize();
if( eRes != openni::STATUS_OK )
{
std::cerr << openni::OpenNI::getExtendedError() << std::endl;
return -1;
}如果函式有正確執行的話,所得到的回傳值會是 openni::STATUS_OK;反過來說,只要回傳值不是 STATUS_OK, 就代表函式執行是有問題的。
而基本上 openni::Status 已經定義的一些常見的錯誤狀況,可以用來做進一步處理的判斷。不過如果是想要得到文字性的錯誤說明的話,也可以透過 openni::OpenNI::getExtendedErropr() 這個函式,來取得更完整的錯誤說明文字。不過要注意的是,他取得的會是最後一筆錯誤資訊,如果之後又有呼叫其他函式的話,可能會影響到它的內容。(不過他是 thread-safe 的) 而如果把之前的範例,全部都加上錯誤檢查的話,則會變成類似這樣子:
// STL Header
#include <iostream>
// 1. include OpenNI Header
#include "OpenNI.h"
// using namespace
using namespace std;
using namespace openni;
int main( int argc, char** argv )
{
// 2. initialize OpenNI
if( OpenNI::initialize() == STATUS_OK )
{
// 3. open a device
Device devAnyDevice;
if( devAnyDevice.open( ANY_DEVICE ) == STATUS_OK )
{
// 4. create depth stream
VideoStream streamDepth;
if( streamDepth.create( devAnyDevice, SENSOR_DEPTH ) == STATUS_OK )
{
if( streamDepth.start() == STATUS_OK )
{
// 5 main loop, continue read
VideoFrameRef frameDepth;
for( int i = 0; i < 100; ++ i )
{
// 5.1 get frame
if( streamDepth.readFrame( &frameDepth ) == STATUS_OK )
{
// 5.2 get data array
const DepthPixel* pDepth = (const DepthPixel*)frameDepth.getData();
// 5.3 output the depth value of center point
int idx = frameDepth.getWidth()*(frameDepth.getHeight()+1)/2;
cout << pDepth[idx] << endl;
}
else
{
cerr << "Can not read frame\n";
cerr << OpenNI::getExtendedError() << endl;
}
}
}
else
{
cerr << "Can not start depth stream\n";
cerr << OpenNI::getExtendedError() << endl;
}
streamDepth.destroy();
}
else
{
cerr << "Can not create depth stream\n";
cerr << OpenNI::getExtendedError() << endl;
}
devAnyDevice.close();
}
else
{
cerr << "Can not open device\n";
cerr << OpenNI::getExtendedError() << endl;
}
// 7. shutdown
OpenNI::shutdown();
}
else
{
cerr << "OpenNI initialize error\n";
cerr << OpenNI::getExtendedError() << endl;
}
return 0;
}這裡比較不一樣的是,Heresy 在前面有加上 using namespace openni;, 指定去使用 openni 這個 namespace,所以之後的程式,都可以把 namespace 省略掉;如此一來,程式寫起來會再簡短一點。 當然,上面的寫法也不是唯一的錯誤檢查的方法。像在官方範例「SimpleRead」裡面,採用的就是另一種程式風格的流程,有興趣的也可以看看。要採用哪種,基本上就是看人習慣了~只是另外也要提一下,理論上在出現錯誤時,main() 應該也要回傳非 0 的錯誤代碼的,Heresy 這邊沒有特別去處理這一塊就是了。
不過…既然都是 C++ 的 API 了,沒有採用 exception(參考)來做處理…Heresy 個人是覺得有點可惜啊…總覺得以各方面來說,OpenNI 的開發團隊,似乎對 C++ 不是很熟悉?雖然 OpenNI 1.x 和 OpenNI 2 都提供了 C++ 的 API,但是實際上,很多介面設計的方式,都還是用 C 的形式來做的…還是其實是有其他考量?所以甚至連陣列都是另外寫一個自己的版本(openni::Array),而沒有直接採用 STL 的版本(也沒有 iterator 可以用)…
【本文來自 Heresy's Space 的網誌,原文網址為: http://kheresy.wordpress.com/2012/12/26/openni-error-handle/ ,由 Heresy 捐出網誌給程式人雜誌,經陳鍾誠編輯後納入雜誌】
人工神經網路 (Artificial Neural Network) (作者:Bridan)
NEURO 這門學問是我工作時才學習得的知識,多年前曾有一篇 洗衣機 貼文提到它,當時第一次知道這東西時,已經從研究所畢業好幾年,書局也沒幾本書可以參考,書中一堆數學式,有看沒有很懂,九O年代網路剛興起,沒甚麼資料可查,正好一位大學同學在大同工學院攻讀博士班主攻語音辨識,NEURO 就是用於學習辨識語音模式的解決方案之一,因此跟主管提出學習計畫,對授課教授表達旁聽的想法,就每周固定時間去大同工學院上課,我不需要學分,所以不用繳學費、不必考試、不必交作業,自備課本上了一個學期的課,這種學習方法在我準備插班大學考試也用過,並認識一些朋友。最近上網查,沒什麼人對 NEURO 議題,提供簡單的實例,以供初學者參考入門,現在將個人所知的做個紀錄分享。
類神經網路有很多解決方案,這裡使用 BP 方法。首先認識神經元的數學模型,
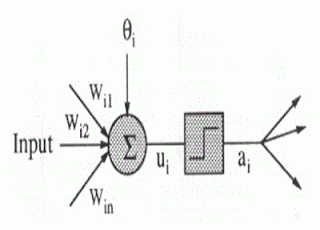
MP (MultiLayer Perceptron) 模型公式:
一、先計算內部數值
Ui = Σ Wji Xj – θi
Wji = 連結強度
Xj = 神經元 j 所傳來之訊號
θi = 神經元 i 之閥值
二、計算輸出數值
Yi = f(Ui) = Yi 處理單元函數
f = 轉換函數,通常為階梯函數(Step function)
例如 Yi = 1 / (1 + exp(-Ui))
三、δ差距量 ,用來修正權重
{T}目標輸出量
{Y}推論輸出量
差距量 = 目標輸出量 – 推論輸出量 = δi = Ti – Yi
本文範例採取的修正算式 δi = Yi‧(1 - Yi)‧(Ti – Yi)
四、計算輸出閥值及權重變量
η:學習速率,控制權重修正幅度
輸出單元閥值改變量 = △θi = - η‧δi
權重改變量 = △Wji = Xj‧η‧δi
五、修正下一輪閥值及權重
θi = θi + △θi
Wji = Wji + △Wji
六、檢驗成果
總錯誤率 = 誤分類案例總數/範例總數
依問題的複雜層度,利用它組合一知識神經網路,基本上有三大層-輸入層、隱藏層及輸出層。
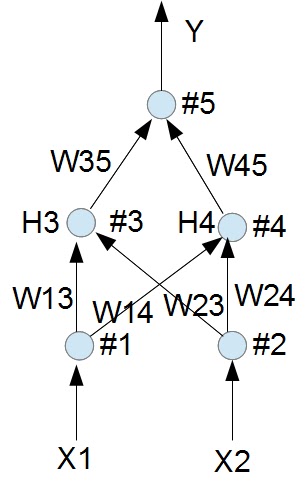
最後整理一個 試算表 提供有興趣的朋友參考,以 XOR 邏輯為例,X1, X2 為輸入,Y為輸出,用 #3, #4, #5 三個神經元學習,H3, H4 是隱藏層(夾在輸入及輸出之間),簡單的問題一個隱藏層就夠,複雜的可能需要兩層。使用四種組合狀態重複訓練,最後它會穩定判別輸入,並給予適合的答案。
以 遞迴或遞歸 (Recursion) 這樣技術,可將非線性數學問題收斂求解, 能處理類似邏輯型式的問題 ,供大家參考。
(本文來自「研發養成所」 Bridan 的網誌,原文網址為 http://4rdp.blogspot.tw/2013/10/artificial-neural-network.html ,由陳鍾誠編輯後納入程式人雜誌)
Visual Basic 6.0:利用遞迴與程序導向解 N Queens Puzzle 皇后問題 (作者:廖憲得 0xde)
什麼是 N Queens Puzzle 皇后問題問題? 通常我們都會用 8 皇后來稱呼它,但將 8 改成動態數字 n,則稱為 n 皇后
什麼是 8 Queens Puzzle 皇后問題問題?
那麼 8 皇后問題又是什麼呢?
八皇后問題是一個以西洋棋為背景的問題:如何能夠在8×8的西洋棋棋盤上放置八個皇后,使得任何一個皇后都無法直接吃掉其他的皇后? 為了達到此目的,任兩個皇后都不能處於同一條橫行、縱行或斜線上。 八皇后問題可以推廣為更一般的n皇后擺放問題 :這時棋盤的大小變為n × n ,而皇后個數也變成n 。 若且唯若 n = 1或n ≥ 4時問題有解[1] 。

5 皇后總共有 10 組解

8 皇后總共有 92 組解
【1皇后】共1組解
【2皇后】共0組解
【3皇后】共0組解
【4皇后】共2組解
【5皇后】共10組解
【6皇后】共4組解
【7皇后】共40組解
【8皇后】共92組解
【9皇后】共352組解
【10皇后】共724組解
【11皇后】共2680組解
【12皇后】共14200組解
【13皇后】共73712組解
【14皇后】共365596組解
【15皇后】共2279184組解
【16皇后】共14772512組解 通常跑超過 10 皇后就需要等待不少時間了!
如何使用遞迴與程序導向去實作呢?
Dim QueenXY() ' 棋盤
Dim TempQueenXY(9999) ' 暫存的棋盤
Dim TempNumber ' 數量
Dim QueenNumber ' 正解總數
Private Sub Form_Activate()
Queen = 9 ' 皇后數
ReDim QueenXY(Queen - 1, Queen - 1) ' 配置棋盤
For I = 0 To Queen - 1
For J = 0 To Queen - 1
QueenXY(I, J) = 0
Next J
Next I
QueenNumber = 0
List1.Clear
For I = 0 To UBound(QueenXY)
Call InputQueen(I, 0)
Next I
MsgBox "總解有 => " & QueenNumber & " 組"
End Sub
Function InputQueen(X, Y) ' 放置皇后
If X >= 0 And X <= UBound(QueenXY) And Y >= 0 And Y <= UBound(QueenXY) Then ' 判斷棋盤是否超過
If QueenXY(X, Y) = 0 Then ' 判斷是否為可放 (是否被殺)
BackupTemp ' Step 備份目前棋盤狀
Call KillQueen(X, Y) ' 建立被殺
For I = 0 To UBound(QueenXY) ' 放下一個
Call InputQueen(I, Y + 1)
Next I
If Y = UBound(QueenXY) Then
QueenNumber = QueenNumber + 1
Temp = ""
List1.AddItem "第 " & QueenNumber & " 組答案為:"
For I = 0 To UBound(QueenXY)
For J = 0 To UBound(QueenXY)
Temp = Temp & QueenXY(I, J) & " "
Next J
List1.AddItem Temp
Temp = ""
Next I
List1.AddItem ""
End If
Reductive ' 還原
End If
End If
End Function
Function KillQueen(KX, KY) ' 跟自己八方被殺
QueenXY(KX, KY) = "Q"
For I = 0 To UBound(QueenXY)
For J = 0 To UBound(QueenXY)
If I = KX And J = KY Then
Else
If I = KX Or J = KY Then QueenXY(I, J) = 1 ' 四面
If (J - KY) <> 0 And (I - KX) <> 0 Then ' 不為 0 (自己)
If Abs((J - KY) / (I - KX)) = 1 Then QueenXY(I, J) = 1 ' 八方 (斜率絕對值 = 1)
End If
End If
Next J
Next I
End Function
Function BackupTemp() ' 備份
Temp = ""
For I = 0 To UBound(QueenXY)
For J = 0 To UBound(QueenXY)
Temp = Temp & QueenXY(I, J) & ","
Next J
Next I
TempQueenXY(TempNumber) = Temp
TempNumber = TempNumber + 1
End Function
Function Reductive() ' 還原
Temp = Split(TempQueenXY(TempNumber - 1), ",")
TempI = 0
For I = 0 To UBound(QueenXY)
For J = 0 To UBound(QueenXY)
QueenXY(I, J) = Temp(TempI)
TempI = TempI + 1
Next J
Next I
TempNumber = TempNumber - 1
End Function- 原始碼下載: N皇后(N Queen).rar
【本文作者為「廖憲得」,原文網址為: http://www.dotblogs.com.tw/0xde/archive/2013/11/11/127531.aspx ,由陳鍾誠編輯後納入本雜誌】
開放電腦計畫 (10) – J0C 編譯器:使用 node.js + javascript 實作 (作者:陳鍾誠)
在 開放電腦計畫的前九篇文章中,我們首先介紹了整體架構,接著設計出了 CPU0 的指令集,然後寫出了 AS0 組譯器與 VM0 虛擬機:
- 開放電腦計畫 (1) – 整體架構與 CPU0 處理器
- 開放電腦計畫 (2) – AS0 組譯器:使用 JavaScript+Node.js 實作
- 開放電腦計畫 (3) – VM0 虛擬機:使用 JavaScript+Node.js 實作
接著我們用 Verilog 設計了一連串的 CPU,主要包含 32 位元的 CPU0 與 16 位元的 MCU0 等處理器。
但是、直到目前為止,我們都還沒有為開放電腦計畫打造出「高階語言」,因此本文將設計出一個 名為 J0 的高階語言 (代表JavaScript 的精簡版),並採用 JavaScript 去實作,然後在 node.js 平台中執行。
有了 J0 語言與 J0C 編譯器之後,我們就可以創建出以下的工具鏈:
J0 語言 ( j0c 編譯器) => IR0 中間碼 (ir2as 轉換器) => CPU0 組合語言 (AS0 組譯器) => CPU0 機器碼 (VM0 虛擬機執行或 CPU0 FPGA 執行)
JavaScript 簡化版 -- J0 語言
以下是一個 J0 語言的程式範例,支援了 function, while, if, for 等語句,並且支援了「陣列與字典」等資料結構。
檔案:test.j0
s = sum(10);
function sum(n) {
s = 0;
i=1;
while (i<=10) {
s = s + i;
i++;
}
return s;
}
m = max(3,5);
function max(a, b) {
if (a > b)
return a;
else
return b;
}
function total(a) {
s = 0;
for (i in a) {
s = s + a[i];
}
return s;
}
a = [ 1, 3, 7, 2, 6];
t = total(a);
word = { e:"dog", c:"狗" };原始碼
接著我們用 node.js + javascript 實作出 j0c 編譯器,該編譯器可以將 J0 語言的程式,編譯成一種平坦化的中間碼格式,我們稱這種格式為 IR0,也就是 Intermediate Representation 0 的意思,以下是 j0c 編譯器的完整程式碼。
檔案:j0c.js
// j0c 編譯器,用法範例: node j0c test.j0
var fs = require("fs");
var util = require("util");
var log = console.log; // 將 console.log 名稱縮短一點
var format = util.format; // 字串格式化
var tokens = [];
var tokenIdx = 0;
var end = "$END";
var funcName = "main";
var funcStack = [ funcName ];
var irText = "";
var symTable = {};
symTable[funcName] = { type:"function", name:"main", pcodes:[] };
var scan=function(text) {
var re = new RegExp(/(\/\*[\s\S]*?\*\/)|(\/\/[^\r\n])|(".*?")|(\d+(\.\d*)?)|([a-zA-Z]\w*)|([>=<!\+\-\*\/&%|]+)|(\s+)|(.)/gm);
var types = [ "", "COMMENT", "COMMENT", "STRING", "INTEGER", "FLOAT", "ID", "OP2", "SPACE", "CH" ];
tokens = [];
tokenIdx = 0;
var lines = 1, m;
while((m = re.exec(text)) !== null) {
var token = m[0], type;
for (i=1; i<=9; i++) {
if (m[i] !== undefined)
type = types[i];
}
if (!token.match(/^[\s\r\n]/) && type!="COMMENT") {
tokens.push({ "token":token, "type":type, "lines":lines });
}
lines += token.split(/\n/).length-1;
}
tokens.push({ "token": end, "type":end, "lines":lines });
return tokens;
}
var error=function(expect) {
var token = tokens[tokenIdx];
log("Error: line=%d token (%s) do not match expect (%s)!", token.lines, token.token, expect);
log(new Error().stack);
process.exit(1);
}
var skip=function(o) { if (isNext(o)) next(o); }
var next=function(o) {
if (o==null || isNext(o)) {
return tokens[tokenIdx++].token;
}
error(o);
}
var isNext=function(o) {
if (tokenIdx >= tokens.length)
return false;
var token = tokens[tokenIdx].token;
if (o instanceof RegExp) {
return token.match(o);
} else
return (token == o);
}
var nextType=function(o) {
if (o==null || isNextType(o)) {
return tokens[tokenIdx++].token;
}
error(o);
}
var isNextType=function(pattern) {
var type = tokens[tokenIdx].type;
return (("|"+pattern+"|").indexOf("|"+type+"|")>=0);
}
var pcode=function(label, op, p, p1, p2) {
symTable[funcName].pcodes.push({"label":label, "op":op, "p":p, "p1":p1, "p2":p2});
var irCode = format("%s\t%s\t%s\t%s\t%s", label, op, p, p1, p2);
log(irCode);
irText += irCode+"\n";
}
var tempIdx = 1;
var nextTemp=function() {
var name="T"+tempIdx++;
symTable[name] = { type:"var", name:name };
return name;
}
var labelIdx = 1;
var nextLabel=function() { return "L"+labelIdx++; }
var elseIdx = 1;
var nextElse=function() { return "else"+elseIdx++; }
var compile=function(text) {
scan(text);
PROG();
}
// PROG = STMTS
var PROG=function() {
STMTS();
}
// STMTS = STMT*
var STMTS=function() {
while (!isNext("}") && !isNext(end))
STMT();
}
// BLOCK = { STMTS }
var BLOCK=function() {
next("{");
STMTS();
next("}");
}
// STMT = FOR | WHILE | IF | FUNCTION | return EXP ; | ASSIGN ; | BLOCK
var STMT=function() {
if (isNext("for")) {
FOR();
} else if (isNext("while")) {
WHILE();
} else if (isNext("if")) {
IF();
} else if (isNext("function")) {
FUNCTION();
} else if (isNext("return")) {
next("return");
var e = EXP();
pcode("", "return", e, "", "");
next(";");
} else if (isNext("{")) {
BLOCK();
} else {
ASSIGN();
next(";");
}
}
// FOR = for (ID in EXP) BLOCK
var FOR=function() {
var startLabel = nextLabel(), exitLabel = nextLabel();
next("for");
next("(");
var id = nextType("ID");
pcode("", "=", id, "0", "");
next("in");
var e=EXP();
next(")");
var t = nextTemp();
pcode(startLabel, "<", t, id, e+".length");
pcode("", "if0", t, exitLabel, "");
BLOCK();
pcode("", "goto", startLabel, "", "");
pcode(exitLabel, "", "", "", "");
}
// WHILE = while (EXP) BLOCK
var WHILE=function() {
var startLabel = nextLabel(), exitLabel=nextLabel();
pcode(startLabel, "", "", "", "");
next("while");
next("(");
var e = EXP();
next(")");
pcode("", "if0", e, exitLabel, "");
BLOCK();
pcode("", "goto", startLabel, "", "");
pcode(exitLabel, "", "", "", "");
}
// IF = if (EXP) STMT (else STMT)?
var IF=function() {
next("if");
next("(");
var e = EXP();
next(")");
var elseLabel = nextLabel();
pcode("", "if0", e, elseLabel, "");
STMT();
if (isNext("else")) {
next("else");
pcode(elseLabel, "", "", "", "");
STMT();
}
}
// ASSIGN = ID[++|--]?(=EXP?)?
var ASSIGN=function() {
var id, op, hasNext = false;
if (isNextType("ID")) {
id = nextType("ID");
symTable[id] = { type:"var", name:id };
if (isNext("++") || isNext("--")) {
var op = next(null);
pcode("", op, id, "", "");
}
hasNext = true;
}
if (isNext("=")) {
next("=");
var e = EXP();
if (id != undefined)
pcode("", "=", id, e, "");
hasNext = true;
}
if (!hasNext)
return EXP();
}
// EXP=TERM (OP2 TERM)?
var EXP=function() {
t1 = TERM();
if (isNextType("OP2")) {
var op2 = next(null);
t2 = TERM();
var t = nextTemp();
pcode("", op2, t, t1, t2);
t1 = t;
}
return t1;
}
// TERM=STRING | INTEGER | FLOAT | ARRAY | TABLE | ID (TERMS)? | ID [TERMS]?| ( EXP )
var TERM=function() {
if (isNextType("STRING|INTEGER|FLOAT")) {
return next(null);
} else if (isNext("[")) {
return ARRAY();
} else if (isNext("{")) {
return TABLE();
} else if (isNextType("ID")) { // function call
var id = next(null);
if (isNext("(")) {
next("(");
while (!isNext(")")) {
// TERM();
var arg = next(null);
pcode("", "arg", arg, "", "");
skip(",");
}
next(")");
var ret = nextTemp();
pcode("", "call", ret, id, "");
return ret;
}
var array = id;
if (isNext("[")) {
next("[");
while (!isNext("]")) {
var idx = TERM();
var t = nextTemp();
pcode("", "[]", t, array, idx);
skip(",");
array = t;
}
next("]");
return array;
}
return id;
} else if (isNext("(")) {
next("(");
var e = EXP();
next(")");
return e;
} else error();
}
// FUNCTION = function ID(ARGS) BLOCK
var FUNCTION = function() {
next("function");
funcName = nextType("ID");
funcStack.push(funcName);
symTable[funcName] = { type:"function", name:funcName, pcodes: [] };
pcode(funcName, "function", "", "", "");
next("(");
while (!isNext(")")) {
var arg=nextType("ID");
pcode("", "param", arg, "", "");
skip(",");
}
next(")");
BLOCK();
pcode("", "endf", "", "", "");
funcStack.pop();
funcName = funcStack[funcStack.length-1];
}
// ARRAY = [ TERMS ];
var ARRAY = function() {
next("[");
var array = nextTemp();
pcode(array, "array", "", "", "");
while (!isNext("]")) {
var t = TERM();
pcode("", "push", array, t, "");
skip(",");
}
next("]");
return array;
}
// TABLE = { (TERM:TERM)* }
var TABLE = function() {
next("{");
var table = nextTemp();
pcode(table, "table", "", "", "");
while (!isNext("}")) {
var key = TERM();
next(":");
var value = TERM();
skip(",");
pcode("", "map", table, key, value);
}
next("}");
return table;
}
var source = fs.readFileSync(process.argv[2], "utf8");
compile(source);執行結果
然後、我們可以用 node.js 來執行上述程式,並且編譯指定的 J0 程式檔,例如以下指令就用 j0c 編譯器去編譯了 test.j0 這個輸入檔,接著畫面上所輸出的就是 IR0 的中間碼。
D:\Dropbox\Public\web\oc\code\js>node j0c test.j0
arg 10
call T1 sum
= s T1
sum function
param n
= s 0
= i 1
L1
<= T2 i 10
if0 T2 L2
+ T3 s i
= s T3
++ i
goto L1
L2
return s
endf
arg 3
arg 5
call T4 max
= m T4
max function
param a
param b
> T5 a b
if0 T5 L3
return a
L3
return b
endf
total function
param a
= s 0
= i 0
L4 < T6 i a.length
if0 T6 L5
[] T7 a i
+ T8 s T7
= s T8
goto L4
L5
return s
endf
T9 array
push T9 1
push T9 3
push T9 7
push T9 2
push T9 6
= a T9
arg a
call T10 total
= t T10
T11 table
map T11 e "dog"
map T11 c "狗"
= word T11
結語
在開放電腦計劃中,我們希望透過 J0 語言,以及 j0c 編譯器,用簡易的程式揭露「高階語言與編譯器」的設計原理。
在下期中,我們將撰寫程式去將上述 IR0 中間碼轉換為 CPU0 的組合語言,這樣就可以接上先前所作的組譯器 AS0 與虛擬機 VM0,以形成一套簡易但完整的工具鏈。
透過這樣的工具鏈,我們希望能讓熟悉程式人輕易的學會「電腦軟硬體的設計原理」。
雜誌訊息
讀者訂閱
程式人雜誌是一個結合「開放原始碼與公益捐款活動」的雜誌,簡稱「開放公益雜誌」。開放公益雜誌本著「讀書做善事、寫書做公益」的精神,我們非常歡迎程式人認養專欄、或者捐出您的網誌,如果您願意成為本雜誌的專欄作家,請加入 程式人雜誌社團 一同共襄盛舉。
我們透過發行這本雜誌,希望讓大家可以讀到想讀的書,學到想學的技術,同時也讓寫作的朋友的作品能產生良好價值 – 那就是讓讀者根據雜誌的價值捐款給慈善團體。 讀雜誌做公益也不需要有壓力,您不需要每讀一本就急著去捐款,您可以讀了十本再捐,或者使用固定的月捐款方式,當成是雜誌訂閱費,或者是季捐款、一年捐一次等都 OK ! 甚至是單純當個讀者我們也都很歡迎!
本雜誌每期參考價:NT 50 元,如果您喜歡本雜誌,請將書款捐贈公益團體。例如可捐贈給「羅慧夫顱顏基金會 彰化銀行(009) 帳號:5234-01-41778-800」。(若匯款要加註可用「程式人雜誌」五個字)
投稿須知
給專欄寫作者: 做公益不需要有壓力。如果您願意撰寫專欄,您可以輕鬆的寫,如果當月的稿件出不來,我們會安排其他稿件上場。
給網誌捐贈者: 如果您沒時間寫專欄或投稿,沒關係,只要將您的網誌以 [創作共用的「姓名標示、非商業性、相同方式分享」授權] 並通知我們,我們會自動從中選取需要的文章進行編輯,放入適當的雜誌當中出刊。
給文章投稿者: 程式人雜誌非常歡迎您加入作者的行列,如果您想撰寫任何文章或投稿,請用 markdown 或 LibreOffice 編輯好您的稿件,並於每個月 25 日前投稿到程式人雜誌社團 的檔案區,我們會盡可能將稿件編入隔月1號出版程式人雜誌當中,也歡迎您到社團中與我們一同討論。
如果您要投稿給程式人雜誌,我們最希望的格式是採用 markdown 的格式撰寫,然後將所有檔按壓縮為 zip 上傳到社團檔案區給我們, 如您想學習 markdown 的撰寫出版方式,可以參考 看影片學 markdown 編輯出版流程 一文。
如果您無法採用 markdown 的方式撰寫,也可以直接給我們您的稿件,像是 MS. Word 的 doc 檔或 LibreOffice 的 odt 檔都可以,我們 會將這些稿件改寫為 markdown 之後編入雜誌當中。
參與編輯
您也可以擔任程式人雜誌的編輯,甚至創造一個全新的公益雜誌,我們誠摯的邀請您加入「開放公益出版」的行列,如果您想擔任編輯或創造新雜誌,也歡迎到 程式人雜誌社團 來與我們討論相關事宜。
公益資訊
| 公益團體 | 聯絡資訊 | 服務對象 | 捐款帳號 |
|---|---|---|---|
| 財團法人羅慧夫顱顏基金會 | http://www.nncf.org/ 02-27190408分機 232 |
顱顏患者 (如唇顎裂、小耳症或其他罕見顱顏缺陷) | 銀行:009彰化銀行民生分行 帳號:5234-01-41778-800 |
| 社團法人台灣省兒童少年成長協會 | http://www.cyga.org/ 04-23058005 |
單親、隔代教養.弱勢及一般家庭之兒童青少年 | 銀行:新光銀行 戶名:台灣省兒童少年成長協會 帳號:103-0912-10-000212-0 |