多層感知器與反傳遞演算法實作 - 使用 JavaScript+Node.js
前言
在前一篇文章中，我們討論了「單層感知器」的實作方式，然而單層感知器並沒有辦法處理像 XOR 這樣的函數。
為了提升「感知器」的能力，我們可以在輸入與輸出節點之間，再加入一些隱藏層，並透過這些隱藏層對整個學習空間進行更多次的分割，以便能處理 XOR 這類難以用單一線性函數分割的問題。
但是加入了隱藏層之後，感知器的學習與訓練就更為複雜了，這時必須有足夠的「數學理論」才能為「多層感知器」提供一個方向，而「反傳遞演算法」 (Back-Propagation) 正是這樣一個可以提供「多層感知器」學習方向的好東西，其數學基礎則是建構在多變數微分「梯度」概念之上的一種「梯度下降法」。
事實上、反傳遞演算法 (Back-Propagation) 的概念在 1974 年就由 Paul J. Werbos 所提出來了，但沒有受到重視，後來在 1986 年又被 Rumelhart 重新發明了出來，而且受到了廣泛的重視。
在本文中，我們將說明「多層感知器」與「反傳遞演算法」的概念，並用 Node.js+JavaScript 進行實作。
模型與數學原理
以下是本文程式所採用的一個「多層感知器」模型，其中包含「輸入層、隱藏層與輸出層」，這種多層感知器與上一篇「單層感知器」的一個明顯不同點，在於擁有一個隱藏層，因此其能力增強了很多。
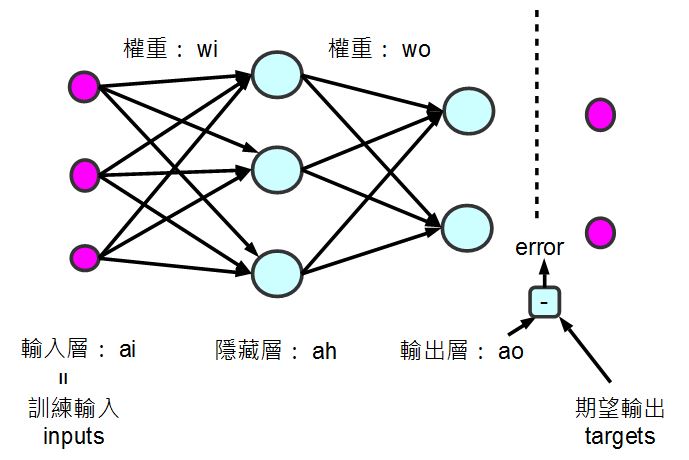
圖、多層感知器模型 (本圖含一個隱藏層)
既然反傳遞演算法是一種梯度下降法，那麼我們只要能計算出梯度的方向，就能讓「多層感知器」的權重朝著能量下降最快的方向前進。
但是、梯度要怎麼計算呢？先讓我們來看一張多變數的能量曲線圖。
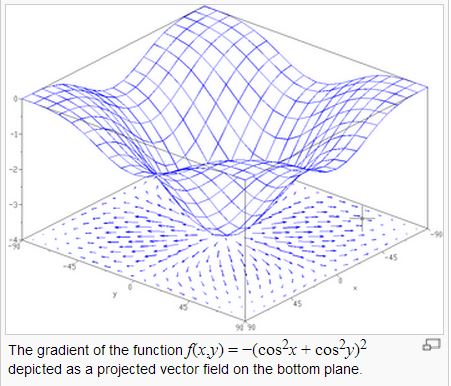
圖、曲面與每一點的梯度向量
在上圖中，底下的平面上所畫的向量，就是上面那個曲面在該點梯度的投影，指示了該平面最陡的下降方向。
在直覺概念上，曲面上某一點的梯度，其實是曲面在該點切平面的法向量，梯度的計算公式如下：
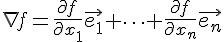
如果我們可以計算某函數之梯度的話，只要朝著梯度的方向走去，就是最快下降的道路了。
採用這種沿著梯度方向往下走的方法，就稱為「梯度下降法」(Gradient Descent)，這種方法可以說是一種「貪婪演算法」(Greedy Algorithm)，因為它每次都朝著最斜的方向走去，企圖得到最大的下降幅度。
為了要計算梯度，我們不能採用「單層感知器裏的那種不可微分的 sign() 步階函數」 (如下圖 a 所示)，因為這樣就不能用微積分的方式計算出梯度了，而必須改用可以微分的連續函數 sigmoid() (如下圖 b 所示)，這樣才能夠透過微分計算出梯度。
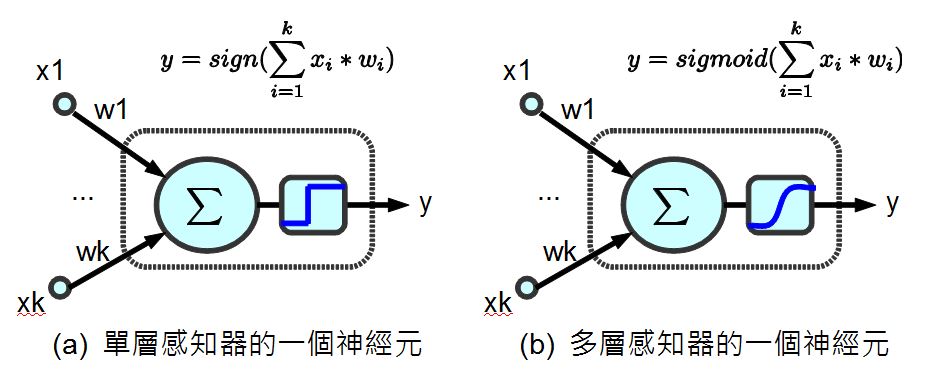
圖、兩種神經元之比較
當我們改成可微分的 sigmoid() 函數之後，就可以運用微積分公式，事先求出其微分函數 dsigmoid() 。舉例而言、在本文的程式中，我們就用了雙曲正切函數 tanh(x) 作為 sigmoid() 函數，其定義如下所示：
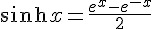
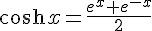
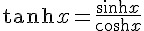
由於 tanh(x) 的微分是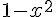 
，因此在下列這段程式中，我們定義了這些函數的計算方式。
var tanh=function(x) {
return (Math.exp(x) - Math.exp(-x)) / (Math.exp(x) + Math.exp(-x));
}
function sigmoid(x) {
return tanh(x); // 表現較好
}
function dsigmoid(x) {
return 1.0 - x*x;
}上述程式中 dsigmoid(y) 中的 1.0 - x*x 則是 y=tanh(x) 的微分式，對每個 y=tanh(x) 都取微分式的時候，其實就是梯度的方向。
(筆者註：有些實作會採用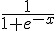 
作為 sigmoid() 函數，這與 tanh(x) 函數的形狀非常類似，也是一種可行的方法)。
程式碼
檔案：backprop.js
// Back-Propagation Neural Networks (JavaScript 版)
// 由陳鍾誠修改自 Neil Schemenauer 的 Python 版
// Python 程式網址為： http://arctrix.com/nas/python/bpnn.py
var log = console.log;
// 建立大小為 n 的陣列並填入初始值 fill
var makeArray=function(n, fill) {
var a = [];
for (var i=0; i<n; i++)
a.push(fill);
return a;
}
// 建立大小為 I*J 的矩陣並填入初始值 fill
var makeMatrix=function(I, J, fill) {
var m = [];
for (var i=0; i<I; i++)
m.push(makeArray(J, fill));
return m;
}
// numbersToStr():以精確度為 precision 個小數來輸出陣列 array
var numbersToStr=function(array, precision) {
var rzStr = "";
for (var i=0; i<array.length; i++) {
if (array[i]>=0)
rzStr+=" "+array[i].toFixed(precision)+" ";
else
rzStr+=array[i].toFixed(precision)+" ";
}
return rzStr;
}
// rand():取得 a 到 b 之間的一個隨機亂數
var rand=function(a, b) {
return (b-a)*Math.random() + a;
}
// sigmoid(x)=tanh(x)
function sigmoid(x) {
var tanh = (Math.exp(x) - Math.exp(-x)) / (Math.exp(x) + Math.exp(-x));
return tanh; // 雙曲正切函數
}
// dsigmoid(x)=1-x^2;
// 參考：http://pynopticon.googlecode.com/svn/trunk/src/vlfeat/toolbox/special/dsigmoid.m
// 參考：http://en.wikipedia.org/wiki/Sigmoid_function
function dsigmoid(x) {
return 1.0 - x*x;
}
function NeuralNet() {
// init()：設定網路結構與權重的隨機初始值的函數。
this.init=function(ni, nh, no) {
// number of input, hidden, and output nodes
this.ni = ni + 1; // +1 for bias node
this.nh = nh;
this.no = no;
// activations for nodes : 建立各層的節點陣列
this.ai = makeArray(this.ni, 1.0);
this.ah = makeArray(this.nh, 1.0);
this.ao = makeArray(this.no, 1.0);
// create weights : 建立權重矩陣
this.wi = makeMatrix(this.ni, this.nh, 0.0);
this.wo = makeMatrix(this.nh, this.no, 0.0);
// set them to random vaules : 隨機設定權重初始值。
for (var i=0; i<this.ni; i++)
for (var j=0; j<this.nh; j++)
this.wi[i][j] = rand(-0.2, 0.2);
for (var j=0; j<this.nh; j++)
for (var k=0; k<this.no; k++)
this.wo[j][k] = rand(-2.0, 2.0);
// last change in weights for momentum : 上一次的改變量矩陣，用來當動量以便爬過肩型區域。
this.ci = makeMatrix(this.ni, this.nh, 0.0);
this.co = makeMatrix(this.nh, this.no, 0.0);
return this;
}
// update() : 計算網路的輸出的函數
this.update=function(inputs) {
// input activations : 設定輸入值
for (var i=0; i<this.ni-1; i++)
this.ai[i] = inputs[i];
// hidden activations : 計算隱藏層輸出值 ah[j]
for (var j=0; j<this.nh; j++) {
var sum = 0.0;
for (var i=0; i<this.ni; i++)
sum = sum + this.ai[i] * this.wi[i][j];
this.ah[j] = sigmoid(sum);
}
// output activations : 計算輸出層輸出值 ao[k]
for (var k=0; k<this.no; k++) {
var sum = 0.0;
for (var j=0; j<this.nh; j++)
sum = sum + this.ah[j] * this.wo[j][k];
this.ao[k] = sigmoid(sum);
}
return this.ao; // 傳回輸出層輸出值 ao
}
// backPropagate()：反傳遞學習的函數 (重要)
this.backPropagate = function(targets, rate, moment) {
// calculate error terms for output : 計算輸出層誤差
var output_deltas = makeArray(this.no, 0.0);
for (var k=0; k<this.no; k++) {
var error = targets[k]-this.ao[k];
output_deltas[k] = dsigmoid(this.ao[k]) * error;
}
// calculate error terms for hidden : 計算隱藏層誤差
var hidden_deltas = makeArray(this.nh, 0.0);
for (var j=0; j<this.nh; j++) {
var error = 0.0;
for (var k=0; k<this.no; k++) {
// 注意、在此輸出層誤差 output_deltas 會反傳遞到隱藏層，因此才稱為反傳遞演算法。
error = error + output_deltas[k]*this.wo[j][k];
}
hidden_deltas[j] = dsigmoid(this.ah[j]) * error;
}
// update output weights : 更新輸出層權重
for (var j=0; j<this.nh; j++) {
for (var k=0; k<this.no; k++) {
var change = output_deltas[k]*this.ah[j];
this.wo[j][k] = this.wo[j][k] + rate*change + moment*this.co[j][k];
this.co[j][k] = change;
// print N*change, M*this.co[j][k]
}
}
// update input weights : 更新輸入層權重
for (var i=0; i<this.ni; i++) {
for (var j=0; j<this.nh; j++) {
var change = hidden_deltas[j]*this.ai[i];
this.wi[i][j] = this.wi[i][j] + rate*change + moment*this.ci[i][j];
this.ci[i][j] = change;
}
}
// calculate error : 計算輸出層誤差總合
var error = 0.0;
for (var k=0; k<targets.length; k++)
error = error + 0.5*Math.pow(targets[k]-this.ao[k],2);
return error;
}
// test() : 對真值表 (訓練樣本) 中的每個輸入都印出「網路輸出」與「期望輸出」，以便觀察學習結果是否都正確。
this.test = function(patterns) {
for (var p in patterns) {
var inputs = patterns[p][0];
var outputs= patterns[p][1];
log("%j -> [%s] [%s]", inputs, numbersToStr(this.update(inputs), 0), numbersToStr(outputs, 0));
// this.dump();
}
}
// train(): 主要學習函數，反覆呼叫反傳遞算法
// 參數：rate: learning rate (學習速率), moment: momentum factor (動量常數)
this.train=function(patterns, iterations, rate, moment) {
for (var i=0; i<iterations; i++) {
var error = 0.0;
for (var p in patterns) {
var pat=patterns[p];
var inputs = pat[0];
var targets = pat[1];
var outputs = this.update(inputs);
error = error + this.backPropagate(targets, rate, moment);
}
if (i % 100 == 0)
log('%d:error %j', i, error);
}
}
}
module.exports = NeuralNet; // 匯出 NeuralNet 物件。執行範例 1 : 學習 XOR 函數
檔案：backprop_xor.js
var NN = require("./backprop");
pat = [
[[0,0], [0]],
[[0,1], [1]],
[[1,0], [1]],
[[1,1], [0]]
];
// create a network with two input, two hidden, and one output nodes
nn = new NN().init(2, 2, 1);
// train it with some patterns
nn.train(pat, 1000, 0.5, 0.1);
// test it
nn.test(pat);執行結果：
D:\Dropbox\Public\web\ai\code\neural>node backprop_xor
0:error 1.1411586806597014
100:error 0.15669092345306487
200:error 0.0044566959936791035
300:error 0.0018489705409186357
400:error 0.0011477205633429219
500:error 0.0008277968129286529
600:error 0.0006456614467953627
700:error 0.005231441443909679
800:error 0.0004595906757934737
900:error 0.0003945408066808508
[0,0] -> [ 0 ] [ 0 ]
[0,1] -> [ 1 ] [ 1 ]
[1,0] -> [ 1 ] [ 1 ]
[1,1] -> [-0 ] [ 0 ]執行範例 2 : 學習七段顯示器函數
檔案：backprop_7seg.js
/* 七段顯示器排列圖示
A
F B
G
E C
D
*/
var NN = require("./backprop");
pat = [
// A B C D E F G
[[1,1,1,1,1,1,0], [0,0,0,0]], // 0
[[0,1,1,0,0,0,0], [0,0,0,1]], // 1
[[1,1,0,1,1,0,1], [0,0,1,0]], // 2
[[1,1,1,1,0,0,1], [0,0,1,1]], // 3
[[0,1,1,0,0,1,1], [0,1,0,0]], // 4
[[1,0,1,1,0,1,1], [0,1,0,1]], // 5
[[1,0,1,1,1,1,1], [0,1,1,0]], // 6
[[1,1,1,0,0,0,0], [0,1,1,1]], // 7
[[1,1,1,1,1,1,1], [1,0,0,0]], // 8
[[1,1,1,1,0,1,1], [1,0,0,1]] // 9
];
// create a network with 7 input, 5 hidden, and 4 output nodes
nn = new NN().init(7, 5, 4);
// train it with some patterns
nn.train(pat, 10000, 0.2, 0.01);
// test it
nn.test(pat);執行結果：
D:\Dropbox\Public\web\ai\code\neural>node backprop_7seg
0:error 21.80370718175807
100:error 3.0996784544877736
200:error 2.9554663137424373
300:error 2.9322332121195545
400:error 0.9175505320368402
500:error 0.5911840202045504
600:error 0.6702566860375645
700:error 0.6175745429758741
800:error 0.6073471516556047
900:error 0.601200049561361
1000:error 0.5810463514787689
1100:error 0.5364677212922591
1200:error 0.532025286869445
1300:error 0.46666848524996085
1400:error 0.48129628693742754
1500:error 0.8155362088747744
1600:error 0.5829386518767099
1700:error 0.6944742612114545
1800:error 0.49717362214697597
1900:error 0.40957109669176334
2000:error 0.5388564563993076
2100:error 0.3703582901903478
2200:error 0.5178647638260341
2300:error 0.1764373289120007
2400:error 0.25347246319196093
2500:error 0.33310966813566406
2600:error 0.17106878914718923
2700:error 0.1365002209754472
2800:error 0.1594051132697459
2900:error 0.3070991793860354
3000:error 0.3766039636947747
3100:error 0.3555367190225767
3200:error 0.11555541960454409
3300:error 0.11367500949340971
3400:error 0.12234128181753154
3500:error 0.1675446667610037
3600:error 0.09044262748000728
3700:error 0.08628776394501735
3800:error 0.27906234926518514
3900:error 0.04818459875532369
4000:error 0.062418918530088664
4100:error 0.2804289611800696
4200:error 0.13725495522690973
4300:error 0.12719742994691247
4400:error 0.07177660395615833
4500:error 0.08548411758763816
4600:error 0.03974217740792855
4700:error 0.09595126476746213
4800:error 0.03853494372617759
4900:error 0.06360901767700806
5000:error 0.07246959735102428
5100:error 0.05362418748287888
5200:error 0.04669033343340621
5300:error 0.03270696475959521
5400:error 0.03940008954106113
5500:error 0.047208537352753516
5600:error 0.049368429554604215
5700:error 0.042625347453785954
5800:error 0.056241589618292134
5900:error 0.016798400589135128
6000:error 0.03404851177897533
6100:error 0.028972975396903942
6200:error 0.01572555942490573
6300:error 0.048110746037786964
6400:error 0.039118552165591194
6500:error 0.03954060666366999
6600:error 0.047240563507126423
6700:error 0.013729342899560402
6800:error 0.03734015049471263
6900:error 0.04385222818693631
7000:error 0.038098235270263764
7100:error 0.014325393180305138
7200:error 0.039093361005808284
7300:error 0.011914229228792664
7400:error 0.012490068609142688
7500:error 0.010110888778014877
7600:error 0.017266400583083073
7700:error 0.037972260655506615
7800:error 0.010317947862704183
7900:error 0.02181165885044425
8000:error 0.033354842242808616
8100:error 0.033244707069915634
8200:error 0.02269772865101642
8300:error 0.008219315372175379
8400:error 0.03342460798252796
8500:error 0.008080093519395289
8600:error 0.02466937317542233
8700:error 0.03307092886686206
8800:error 0.033433889409569414
8900:error 0.031423007039930506
9000:error 0.018154152094468162
9100:error 0.008635680953338276
9200:error 0.030890671102892397
9300:error 0.009020762345545542
9400:error 0.015823853695083934
9500:error 0.029353956299920176
9600:error 0.03028116871034789
9700:error 0.03009059907189612
9800:error 0.025996249652393937
9900:error 0.009595759182954272
[1,1,1,1,1,1,0] -> [ 0 0 -0 -0 ] [ 0 0 0 0 ]
[0,1,1,0,0,0,0] -> [ 0 -0 -0 1 ] [ 0 0 0 1 ]
[1,1,0,1,1,0,1] -> [-0 -0 1 0 ] [ 0 0 1 0 ]
[1,1,1,1,0,0,1] -> [-0 0 1 1 ] [ 0 0 1 1 ]
[0,1,1,0,0,1,1] -> [ 0 1 -0 0 ] [ 0 1 0 0 ]
[1,0,1,1,0,1,1] -> [-0 1 -0 1 ] [ 0 1 0 1 ]
[1,0,1,1,1,1,1] -> [-0 1 1 0 ] [ 0 1 1 0 ]
[1,1,1,0,0,0,0] -> [-0 1 1 1 ] [ 0 1 1 1 ]
[1,1,1,1,1,1,1] -> [ 1 -0 -0 0 ] [ 1 0 0 0 ]
[1,1,1,1,0,1,1] -> [ 1 0 -0 1 ] [ 1 0 0 1 ]結語
您可以看到上述兩個訓練案例，都是完全正確的，這代表反傳遞演算法可以讓多層感知器學會 XOR 與七段顯示器的函數。
當然、多層感知器也可以學會更難的問題，像是手寫的數字與英文字辨認等等，手寫中文辨認和語音辨認當然也是可行的，只不過需要很多的訓練範例與節點，學習的效果才會夠好就是了！
參考文獻
【本文由陳鍾誠取材並修改自 維基百科，採用創作共用的 姓名標示、相同方式分享 授權】