前言
編輯小語
在本期的「程式人雜誌」中,聚焦的主題是「爬山演算法」。
「爬山演算法」在人工智慧領域是用來做優化 (最佳化) 的一種簡單演算法。這方法雖然簡單,但是卻非常好用,因此我常用「爬山演算法」來解各式各樣的優化問題。而且在「人工智慧」課程時用「爬山演算法」做為第一個學習的優化算法。
「模擬退火法」則是爬山演算法的一個變形,但在優化的想法上有點不同,爬山演算法顧名思義會不斷的往高處爬,而「模擬退火法」則會不斷的向著能量低的方向走。當我們把爬山的高度轉換成位能函數時,就變成了一種「流水下山演算法」,然後我們再加入用溫度控制的遷移機率之後,可以讓這個演算法有機會跳出谷底,找到另一個更好的解。
當然、本期不只有「爬山演算法」的相關文章,還有更精彩的 Arduino, VB, OpenCV 與擴增實境, 開放電腦計畫等內容,希望讀者會喜歡這期的「程式人雜誌」!
---- (程式人雜誌編輯 - 陳鍾誠)
授權聲明
本雜誌許多資料修改自維基百科,採用 創作共用:姓名標示、相同方式分享 授權,若您想要修改本書產生衍生著作時,至少應該遵守下列授權條件:
- 標示原作者姓名 (包含該文章作者,若有來自維基百科的部份也請一併標示)。
- 採用 創作共用:姓名標示、相同方式分享 的方式公開衍生著作。
另外、當本雜誌中有文章或素材並非採用 姓名標示、相同方式分享 時,將會在該文章或素材後面標示其授權,此時該文章將以該標示的方式授權釋出,請修改者注意這些授權標示,以避免產生侵權糾紛。
例如有些文章可能不希望被作為「商業性使用」,此時就可能會採用創作共用:姓名標示、非商業性、相同方式分享 的授權,此時您就不應當將該文章用於商業用途上。
最後、懇請勿移除公益捐贈的相關描述,以便讓愛心得以持續散播!
本期焦點
從爬山演算法到梯度下降法
爬山演算法 (Hill Climbing) 是一種最簡單的優化算法,該方法就像模擬人類爬山時的行為而設計的,因此稱為爬山演算法。
程式究竟要怎麼爬山呢?且讓我們用一張圖來看看。
假如我們在 Google 裏輸入一個算式,Google 會幫我們畫出該函數。舉例而言,如果我在 Google 輸入 x^2+3x+5 這個算式,您會看到下列圖形:
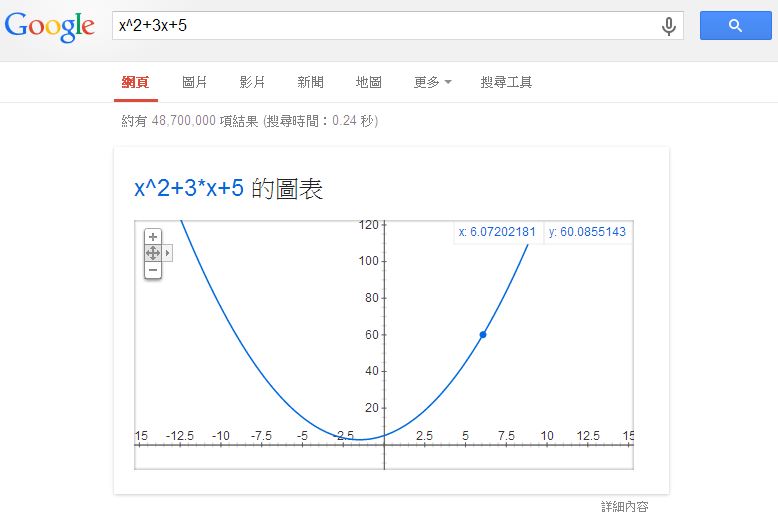
圖、在 Google 輸入 x^2+3x+5 後顯示的函數圖
這時您可以移動滑鼠,圖形會出現一個可移動的小藍點,該點會沿著曲線移動,上圖中 (x, y) 座標顯示為 x:6.07202181, y:60.0855143, 就是那個小藍點所在的位置。
如果我們想要寫程式尋找這個函數的最低點,那我們應該怎麼找呢?
其實方法很簡單,就是一直往低的地方走,一直走到最低點,然後你會看到左右兩邊都沒辦法更低了,於是就停止尋找,傳回該最低點作為答案。
這個方法,就像是水往低處流一樣,不斷的往更低的方向流,最後一定會流到一個山谷,然後就積成一個湖了。
但是、既然這樣,那為甚麼叫做爬山演算法,而不叫「流水下山演算法」呢?
其實、只要反過來看就行了,如果我們想要找的是最高點,而不是最低點,那整個行為就會像爬山一樣,只是最後爬到山頂就會停了。
採用這種想法,若我們想找 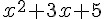 這個函數的最高,我們可以在 Google 輸入
這個函數的最高,我們可以在 Google 輸入 -(x^2+3x+5) 就可以看到那座山了,以下是 Google 顯示的結果:
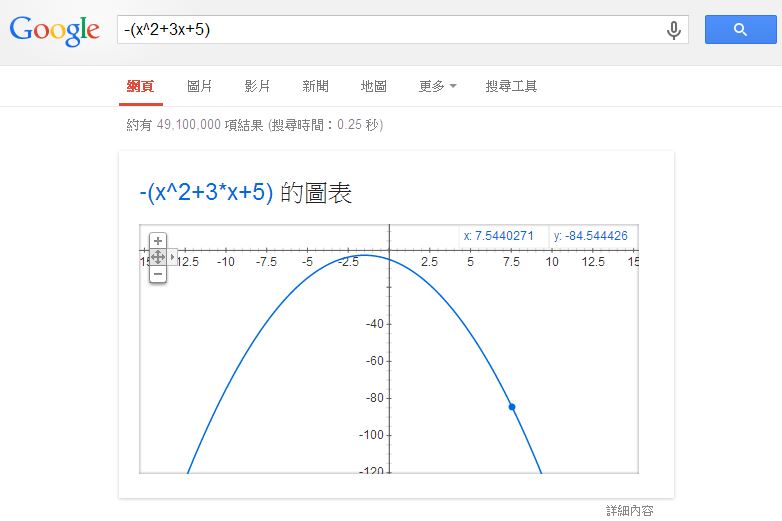
圖、在 Google 輸入 -(x^2+3x+5) 後顯示的函數圖
當然、如果函數有很多山峰,那這種方法只能走到小山丘就會停了。這時您可能會說,那為甚麼不再繼續往更高的山走去呢?
關於這點,並不是不行,只是程式沒有眼睛,也沒辦法一眼望去把所有的地形都給看光,然後知道更高的山峰在哪裡?
如果我們用上面水往低處流的想法,您就會清楚爬山演算法所遭遇的困難了。當您像水一樣往下流,到了谷底之後,由於四周都是山壁,所以您根本看不到更低的谷到底在哪裡,所以只好就停下來了。
此時、除非你爬出山谷,否則根本不可能找到更深的谷,這就是「流水下山演算法」所遭遇到的困難了。以下是我們用 Google 顯示 (x-5)*(x-3)*(2x+5)*(x+3) 這個具有兩個山谷的函數,所得到的圖形。
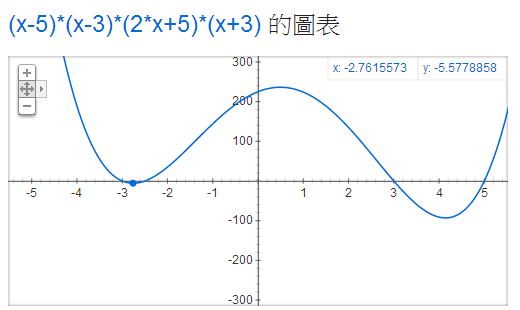
圖、兩個山谷的情況,如何找到最低的山谷呢?
假如我們在上圖中左邊的山谷,那麼怎麼能知道右邊還有一個更低的山谷呢?這就是「流水下山演算法」的困難之所在了!
當然、也有人試圖提出一些企圖找到更深的谷,或爬到更高的山的演算法,這些演算法往往是以爬山演算法為基礎,然後再作一些改良,像是「模擬退火演算法」(Simulated Annealing Algorithm) 或大洪水演算法 (Great Deluge algorithm) 等等,這些方法都是企圖讓「流水下山演算法」有機會跳出山谷而設計的方法。
當然、您也可以企圖加上「衝力」之類的想法讓「流水下山演算法」可以衝出低谷,但是到底要衝多久,還有該往哪個方向衝才對呢?那這種方法是否該改叫「衝山演算法」呢?
當然、我是沒有聽過這種名稱啦!
另外、對於上述的單變數函數而言,不是往左邊走就是往右邊走,但是如果有兩個變數,例如像 x^2+y^2+3x+5y+6 ,但是只有一個山谷,那麼我們該修改哪個變數呢?舉例而言,以下就是 Google 所畫出的 x^2+y^2+3x+5y+6 之圖形。
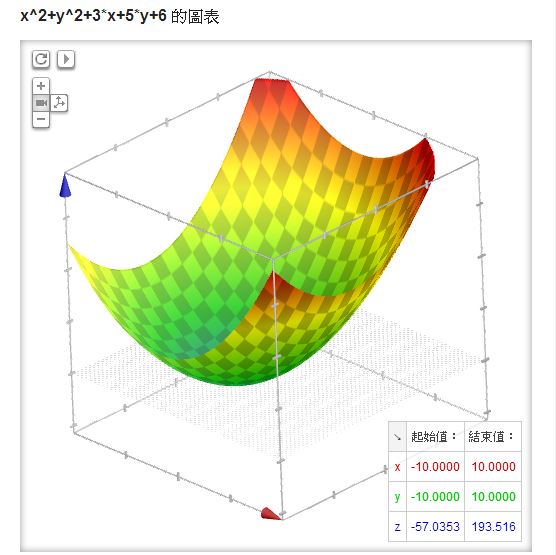
在上述的雙變數情形中,我們可以隨機的挑一個變數,然後向左或向右移動一小步,只要移動後的點更低就接受,如果連續很多次移動都沒辦法找到更低的點,就認為已經到達山谷,這樣的方法其實還蠻有效的,這種方法可以稱為「隨機下山演算法」 (反過來英文中以爬山的角度來看,所以稱為隨機爬山演算法 Stochastic Hill Climbing Algorithm)。
當然、隨機的方法有時會比較沒效率,如果我們可以很容易的透過微積分計算斜率 (導數) 的話,那麼不管幾個變數,我們都可以計算出山坡上最陡峭的那一個方向,這種微積分概念稱為「梯度」,如下圖所示:
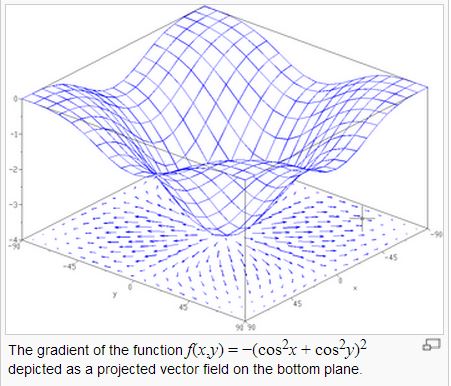
圖、曲面與每一點的梯度向量
在上圖中,底下的平面上所畫的向量,就是上面那個曲面在該點的梯度,換句話說某一點的梯度其實是一個向量。梯度的計算公式如下:
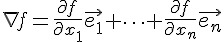
如果我們可以計算某函數之梯度的話,那麼就可以不用透過隨機的方式去亂走了,只要朝著梯度的方向走去,就是最快下降的道路了。
如果我們採用這種沿著梯度方向往下走的方法,就稱為「梯度下降法」(Gradient Descent),這種方法可以說是一種「貪婪演算法」(Greedy Algorithm),因為它每次都朝著最斜的方向走去,企圖得到最大的下降幅度。
在程式人雜誌上一期的焦點「神經網路」中的「反傳遞演算法」,其實就是一種梯度下降法,所以才會有下列這段程式:
function sigmoid(x) {
return ml.tanh(x);
}
function dsigmoid(y) {
return 1.0 - y*y;
}其中的 sigmoid(x) 設定為 tanh(x) 這個函數,tanh(x) 的數學定義如下:
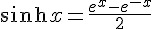
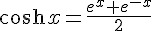
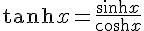
而 dsigmoid(y) 中的 1.0 - y*y 則是 y=tanh(x) 的微分式,對每個 y=tanh(x) 都取微分式的時候,其實就是梯度的方向,因此「反傳遞演算法」事實上是一種梯度下降法啊!
這時,或許各位會想起,「貪婪演算法」怎麼感覺有點熟悉,似乎在哪裡學過?
如果各位學過演算法課程,或許想起像「最小擴展樹」(Minimal Spanning Tree) 的演算法,您會想到這種方法也很貪婪,因為每次都找最小的邊來加入,那也是一種「貪婪演算法」,但這與此處的貪婪演算法之概念顯然有些差距了。
參考文獻
- Wikipedia:Hill climbing
- Wikipedia:Great Deluge algorithm
- Wikipedia:Simulated annealing
- Wikipedia:Stochastic hill climbing
- Wikipedia:Gradient descent
- Wikipedia:Greedy algorithm
- 維基百科:爬山演算法
- 維基百科:模擬退火
- 維基百科:梯度下降法
- 維基百科:貪心法
【本文由陳鍾誠取材並修改自 維基百科,採用創作共用的 姓名標示、相同方式分享 授權】
以爬山演算法尋找函數最高點 - 使用 JavaScript+Node.js 實作
簡介
以下是「爬山演算法」 (Hill-Climbing Algorithm) 的一個簡易版本,其方法超簡單,就是一直看旁邊有沒有更好的解,如果有就移過去。然後反覆的作這樣的動作,直到旁邊的解都比現在的更差時,程式就停止,然後將那個位於山頂的解傳回,就完成了。
Algorithm HillClimbing(f, x)
x = 隨意設定一個解。
while (x 有鄰居 x' 比 x 更高)
x = x';
end
return x;
end當然、這種演算法只能找到「局部最佳解」(local optimal),當整個空間有很多山頂的時候,這種方法會爬到其中一個山頂就停了,並不一定會爬到最高的山頂。
程式碼
檔案: HillClimbingSimple.js
var util = require("util");
var log = console.log;
function f(x) { return -1*(x*x+3*x+5); }
// function f(x) { return -1*Math.abs(x*x-4); }
var dx = 0.01;
function hillClimbing(f, x) {
while (true) {
log("f(%s)=%s", x.toFixed(4), f(x).toFixed(4));
if (f(x+dx) >= f(x))
x = x+dx;
else if (f(x-dx) >= f(x))
x = x-dx;
else
break;
}
}
hillClimbing(f, 0.0);執行結果
求解 : 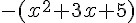 的最高點,也就是
的最高點,也就是 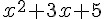 的最低點。
的最低點。
D:\Dropbox\Public\web\ai\code\optimize>node hillClimbingSimple
f(0.0000)=-5.0000
f(-0.0100)=-4.9701
f(-0.0200)=-4.9404
f(-0.0300)=-4.9109
f(-0.0400)=-4.8816
f(-0.0500)=-4.8525
...
f(-1.4500)=-2.7525
f(-1.4600)=-2.7516
f(-1.4700)=-2.7509
f(-1.4800)=-2.7504
f(-1.4900)=-2.7501
f(-1.5000)=-2.7500如果我們將上述程式的 f(x) 換成註解中的那個,也就是將 f(x) 換成如下版本:
function f(x) { return -1*Math.abs(x*x-4); }那麼就可以用來求解 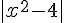 的最低點,也就是尋找 4 的平方根,以下是執行結果:
的最低點,也就是尋找 4 的平方根,以下是執行結果:
D:\Dropbox\Public\web\ai\code\optimize>node hillClimbingSimple
f(0.0000)=-4.0000
f(0.0100)=-3.9999
f(0.0200)=-3.9996
f(0.0300)=-3.9991
f(0.0400)=-3.9984
f(0.0500)=-3.9975
...
f(1.9500)=-0.1975
f(1.9600)=-0.1584
f(1.9700)=-0.1191
f(1.9800)=-0.0796
f(1.9900)=-0.0399
f(2.0000)=-0.0000您可以看到上述程式正確的找到 4 的平方根是 2,而我們所用的方法與求解 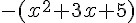 的最高點幾乎是一模一樣的,只是把函數換掉而已。
的最高點幾乎是一模一樣的,只是把函數換掉而已。
結語
您可以看到上述用爬山演算法尋找函數最高點或最低點的程式,其實非常的簡單,只不過是看看兩邊是否有更好的解,如果有就移過去罷了。
但是、這麼簡單的演算法,其實威力是非常強大的,這種方法可以求解的問題非常的多,很多人工智慧上非常重要的問題,其實都只不過是在進行函數優化的動作,也就是尋找某個函數的低點或高點而已,這些問題其實大部分都可以使用爬山演算法來求解。
當然、要能尋找更複雜函數的「區域最佳解」,還必須進一步的對上述程式進行封裝與抽象化,我們將在下一篇文章中解說將上述爬山程式抽象化後的版本,並用該程式來求更複雜函數的解。
參考文獻
【本文由陳鍾誠取材並修改自 維基百科,採用創作共用的 姓名標示、相同方式分享 授權】
通用的爬山演算法架構 - 使用 JavaScript+Node.js 實作
前言
在上一篇文章中,我們介紹了如何用 JavaScript 來尋找「單變數函數」的最高點。在這篇文章中,我們會將這個程式抽象化之後,成為一個通用的爬山演算法架構,以便能夠尋找任何函數的最高點。
通用的爬山演算法架構
檔案:HillClimbing.js
var hillClimbing = function() {} // 爬山演算法的物件模版 (類別)
hillClimbing.prototype.run = function(s, maxGens, maxFails) { // 爬山演算法的主體函數
console.log("s=%s", s); // 印出初始解
var fails = 0; // 失敗次數設為 0
// 當代數 gen<maxGen,且連續失敗次數 fails < maxFails 時,就持續嘗試尋找更好的解。
for (var gens=0; gens<maxGens && fails < maxFails; gens++) {
var snew = s.neighbor(); // 取得鄰近的解
var sheight = s.height(); // sheight=目前解的高度
var nheight = snew.height(); // nheight=鄰近解的高度
if (nheight >= sheight) { // 如果鄰近解比目前解更好
s = snew; // 就移動過去
console.log("%d: %s", gens, s); // 印出新的解
fails = 0; // 移動成功,將連續失敗次數歸零
} else // 否則
fails++; // 將連續失敗次數加一
}
console.log("solution: %s", s); // 印出最後找到的那個解
return s; // 然後傳回。
}
module.exports = hillClimbing; // 將爬山演算法的類別匯出。抽象的解答類別
檔案:solution.js
var Solution = function(v) { // 解答的物件模版 (類別)
this.v = v; // 參數 v 為解答的資料結構
}
Solution.prototype.step = 0.01; // 每一小步預設走的距離
Solution.prototype.height = function() { // 爬山演算法的高度函數
return -1*this.energy(); // 高度 = -1 * 能量
}
module.exports = Solution; // 將解答類別匯出。實例 1 :求解平方根
在此,我們將以求解 4 的平方根為例,測試一下上述演算法是否能夠找到正確的解答。
檔案:solutionNumber.js (單變數函數,求平方根)
var Solution = require("./solution"); // 引入解答類別
Solution.prototype.neighbor = function() { // 單變數解答的鄰居函數。
var x = this.v, dx=this.step; // x:解答 , dx : 移動步伐大小
var xnew = (Math.random() > 0.5)?x+dx:x-dx; // 用亂數決定向左或向右移動
return new Solution(xnew); // 建立新解答並傳回。
}
Solution.prototype.energy = function() { // 能量函數
var x = this.v; // x:解答
return Math.abs(x*x-4); // 能量函數為 |x^2-4|
}
Solution.prototype.toString = function() { // 將解答轉為字串,以供印出觀察。
return "energy("+this.v.toFixed(3)+")="+this.energy().toFixed(3);
}
module.exports = Solution; // 將解答類別匯出。檔案:hillClimbingNumber.js
var hillClimbing = require("./hillClimbing"); // 引入爬山演算法類別
var solutionNumber = require("./solutionNumber"); // 引入平方根解答類別
var hc = new hillClimbing(); // 建立爬山演算法物件
// 執行爬山演算法 (從「解答=0.0」開始尋找, 最多十萬代、失敗一千次就跳出。
hc.run(new solutionNumber(0.0), 100000, 1000);執行結果:
D:\Dropbox\Public\web\ai\code\optimize>node hillClimbingNumber.js
s=energy(0.000)=4.000
0: energy(-0.010)=4.000
2: energy(-0.020)=4.000
3: energy(-0.030)=3.999
10: energy(-0.040)=3.998
12: energy(-0.050)=3.998
....
366: energy(-1.910)=0.352
371: energy(-1.920)=0.314
375: energy(-1.930)=0.275
380: energy(-1.940)=0.236
382: energy(-1.950)=0.197
388: energy(-1.960)=0.158
389: energy(-1.970)=0.119
391: energy(-1.980)=0.080
392: energy(-1.990)=0.040
394: energy(-2.000)=0.000
solution: energy(-2.000)=0.000您可以看到上述程式最後找到 4 的平方根為 -2,這算是對的,因為我們在能量函數中沒有規定平方根必須是正的,如果要求要是正的,那就可以為負數加上一個懲罰函數就行了。
實例 2 :多變數函數的最佳化
在此,我們將以求解 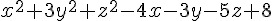 這個函數的最低點,看看上述演算法對多變數函數是否能正常運作。
這個函數的最低點,看看上述演算法對多變數函數是否能正常運作。
檔案:solutionArray.js
var Solution = require("./solution"); // 引入抽象的解答類別
Solution.prototype.neighbor = function() { // 多變數解答的鄰居函數。
var nv = this.v.slice(0); // nv=v.clone()=目前解答的複製品
var i = Math.floor(Math.random()*nv.length);// 隨機選取一個變數
if (Math.random() > 0.5) // 擲骰子決定要往左或往右移
nv[i] += this.step;
else
nv[i] -= this.step;
return new Solution(nv); // 傳回新建的鄰居解答。
}
Solution.prototype.energy = function() { // 能量函數
var x=this.v[0], y=this.v[1], z=this.v[2];
return x*x+3*y*y+z*z-4*x-3*y-5*z+8; // (x^2+3y^2+z^2-4x-3y-5z+8)
}
var numbersToStr=function(array, precision) { // 將數字陣列轉為字串的函數。
var rzStr = "";
for (var i=0; i<array.length; i++) {
if (array[i]>=0)
rzStr+=" "+array[i].toFixed(precision)+" ";
else
rzStr+=array[i].toFixed(precision)+" ";
}
return rzStr;
}
Solution.prototype.toString = function() { // 將解答轉為字串的函數,以供列印用。
return "energy("+numbersToStr(this.v, 3)+")="+this.energy().toFixed(3);
}
module.exports = Solution; // 將解答類別匯出。檔案: hillClimbingArray.js
var hillClimbing = require("./hillClimbing"); // 引入爬山演算法類別
var solutionArray = require("./solutionArray"); // 引入多變數解答類別 (x^2+3y^2+z^2-4x-3y-5z+8)
var hc = new hillClimbing(); // 建立爬山演算法物件
// 執行爬山演算法 (從「解答(x,y,z)=(1,1,1)」開始尋找, 最多十萬代、失敗一千次就跳出。
hc.run(new solutionArray([1,1,1]), 100000, 1000);執行結果
s=energy( 1.000 1.000 1.000 )=1.000
0: energy( 1.000 1.000 1.010 )=0.970
1: energy( 1.000 1.000 1.020 )=0.940
3: energy( 1.000 1.000 1.030 )=0.911
8: energy( 1.000 1.000 1.040 )=0.882
9: energy( 1.000 1.000 1.050 )=0.853
...
889: energy( 2.000 0.500 2.450 )=-2.998
894: energy( 2.000 0.500 2.460 )=-2.998
907: energy( 2.000 0.500 2.470 )=-2.999
917: energy( 2.000 0.500 2.480 )=-3.000
920: energy( 2.000 0.500 2.490 )=-3.000
924: energy( 2.000 0.500 2.500 )=-3.000
solution: energy( 2.000 0.500 2.500 )=-3.000您可以發現這個程式最後找到的解答是 (x, y, z)=(2, 0.5, 2.5),其能量值為 -3,也就是高度值為 3。
實例 3 :線性聯立方程組求解
本範例求解的線性聯立方程組,可以用矩陣描述如下:
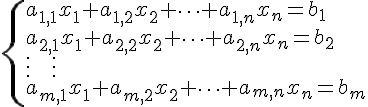
這種線性聯立方程組,可以寫為矩陣相乘的形式如下:
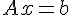
其中的 A 為矩陣、x 與 b 均為「列向量」。
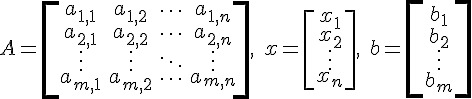
這類問題想要求的答案是 x 的值,也就是在 A 與 b 都已知的情況之下,求符合條件的 x 是多少?
我們使用的測試範例如下:
A=[[1,1],[1,-1]]
B=[[5][1]]也就是求下列方程組的解答。
x1+x2=5
x1-x2=1以下是我們表示解答的程式碼,其中引入了 matrix 這個矩陣相乘的函式庫。
檔案:solutionEquations.js
var Matrix = require("./matrix");
var Solution = require("./solution"); // 引入抽象的解答類別
// A X = B ,求 X 是多少?
// A=[[1,1],[1,-1]] B=[[5][1]],也就是求:
// x1+x2=5
// x1-x2=1
// 的解答
var A = new Matrix([[1,1],[1,-1]]);
var B = new Matrix([[5,1]]).transpose();
var log = console.log;
Solution.zero = function() {
return new Solution(Matrix.create(2,1,0));
}
Solution.prototype.neighbor = function() { // 多變數解答的鄰居函數。
var nx = new Matrix(this.v.m); // 複製目前解的矩陣
var i = Math.floor(Math.random()*nx.rows());// 隨機選取一個變數
if (Math.random() > 0.5) // 擲骰子決定要往左或往右移
nx.m[i][0] += this.step;
else
nx.m[i][0] -= this.step;
return new Solution(nx); // 傳回新建的鄰居解答。
}
Solution.prototype.energy = function() { // 能量函數:計算 ||AX-B||,也就是 ||Y-B||
var X = this.v;
var Y = A.mul(X);
return Y.sub(B).norm();
}
Solution.prototype.toString = function() { // 將解答轉為字串的函數,以供列印用。
return "energy("+this.v.transpose().toString().replace("\n", "")+")="+this.energy().toFixed(3);
}
module.exports = Solution; // 將解答類別匯出。接著是爬山演算法的主體,我們從解答 x=[0,0] 開始尋找:
檔案:hillClimbingEquations.js
var hillClimbing = require("./hillClimbing"); // 引入爬山演算法類別
var solutionEquations = require("./solutionEquations"); // 引入線性聯立方程組解答類別
var hc = new hillClimbing(); // 建立爬山演算法物件
// 執行爬山演算法 (從「解答 x=(0,0)」開始尋找, 最多十萬代、失敗一千次就跳出。
hc.run(solutionEquations.zero(), 100000, 1000);最後我們列出整個矩陣相乘的函數庫原始碼:
檔案:matrix.js
var log = console.log;
var Matrix=function(mat) {
var m = [];
for (var i=0; i<mat.length; i++) {
m[i] = mat[i].slice(0);
}
this.m = m;
}
Matrix.prototype.precision = 3;
Matrix.prototype.toStr=function(precision) {
var rzStr = "", m = this.m;
for (var i=0; i<m.length; i++) {
var rowStr = ""
for (var j=0; j<m[i].length; j++)
rowStr += m[i][j].toFixed(precision)+" ";
rzStr += "["+rowStr.trim()+"]\n";
}
return rzStr;
}
Matrix.prototype.rows=function() { return this.m.length; }
Matrix.prototype.cols=function() { return this.m[0].length; }
Matrix.prototype.toString=function() { return this.toStr(this.precision); }
Matrix.create=function(rows, cols, value) {
var m = [];
for (var i=0; i<rows; i++) {
m[i] = [];
for (var j=0; j<cols; j++)
m[i][j] = value;
}
return new Matrix(m);
}
Matrix.prototype.transpose=function() {
var m = this.m;
var r = Matrix.create(m[0].length, m.length, 0);
for (var i=0; i<m.length;i++) {
for (var j=0; j<m[i].length;j++)
r.m[j][i] = m[i][j];
}
return r;
}
Matrix.prototype.mul=function(mat2) {
var m = this.m, m2=mat2.m;
var r = Matrix.create(m.length, m2[0].length, 0);
for (var i=0; i<m.length;i++)
for (var j=0; j<m[i].length; j++)
for (var k=0; k<m2[j].length; k++)
r.m[i][k] += m[i][j]*m2[j][k];
return r;
}
Matrix.prototype.add=function(mat2) {
var m = this.m, m2 = mat2.m;
var r = Matrix.create(m.length, m[0].length, 0);
for (var i=0; i<m.length; i++)
for (var j=0; j<m[i].length; j++)
r.m[i][j] = m[i][j]+m2[i][j];
return r;
}
Matrix.prototype.sub=function(mat2) {
return this.add(mat2.neg());
}
Matrix.prototype.sum=function() {
var s=0;
for (var i=0; i<m.length; i++)
for (var j=0; j<m[i].length; j++)
s += m[i][j];
return s;
}
Matrix.prototype.norm=function() {
var s=0, m=this.m;
for (var i=0; i<m.length; i++)
for (var j=0; j<m[i].length; j++)
s += m[i][j]*m[i][j];
return s;
}
Matrix.prototype.neg=function() {
var r = Matrix.create(this.rows(), this.cols(), 0);
for (var i=0; i<r.m.length; i++)
for (var j=0; j<r.m[i].length; j++)
r.m[i][j] = -1*this.m[i][j];
return r;
}
Matrix.test=function() {
var m1=new Matrix([[1,1,1], [1,2,3]]);
var m2=m1.transpose();
Matrix.prototype.precision = 0;
log("=====m1========\n%s", m1);
log("=====m2========\n%s", m2);
log("=====m1+m1=====\n%s", m1.add(m1));
log("=====m1*m2=====\n%s", m1.mul(m2));
}
// Matrix.test();
module.exports = Matrix;執行結果如下:
s=energy([0.000 0.000])=26.000
1: energy([0.000 0.010])=25.920
5: energy([0.000 0.020])=25.841
6: energy([0.000 0.030])=25.762
7: energy([0.000 0.040])=25.683
9: energy([0.010 0.040])=25.563
...
655: energy([1.600 1.760])=4.035
656: energy([1.600 1.770])=4.026
659: energy([1.610 1.770])=3.970
660: energy([1.620 1.770])=3.915
661: energy([1.630 1.770])=3.860
664: energy([1.640 1.770])=3.805
665: energy([1.640 1.780])=3.796
666: energy([1.640 1.790])=3.787
...
1176: energy([2.970 2.000])=0.002
1184: energy([2.980 2.000])=0.001
1197: energy([2.990 2.000])=0.000
1205: energy([3.000 2.000])=0.000
solution: energy([3.000 2.000])=0.000您可以看到最後找到的解為 x=[3, 2] ,這個結果確實是下列方程組的解答:
x1+x2=5
x1-x2=1於是我們用這個爬山演算法的架構解決了線性聯立方程組的求解問題。
結語
當然、上述的架構不只可以解這些問題,甚至可以用來解像「線性規劃、神經網路優化....」等等各式各樣的問題,前提是您必須自行設計 solution 類別的 neighbor(), energy() 與 toString() 函數,然後寫個主程式呼叫爬山演算法就行了。
參考文獻
【本文由陳鍾誠取材並修改自 維基百科,採用創作共用的 姓名標示、相同方式分享 授權】
通用的「模擬退火法」架構 - 使用 JavaScript+Node.js 實作
前言
在上一篇文章中,我們介紹了一個通用的爬山演算法架構,而模擬退火法其實是爬山演算法的一個改良版,其設計理念是參考打鐵時金屬從高溫逐漸緩慢降溫,可以讓結構更緊緻的這種概念,在「流水下山演算法」上加入了溫度的概念。
當溫度很高的時候,模擬退火法基本上就像隨機亂走一樣,但是當溫度逐漸下降之後,模擬退火法就會逐漸凝固,只能朝著較好的解前進,向著較差解前進的機率會逐漸縮小。
當溫度幾乎降到零的時候,模擬退火法基本上就會退化成爬山演算法,於是最後還是會固定在某個「區域最佳解」上面。但是由於經過從高溫緩慢降溫的過程,所以模擬退火法比較有機會在高溫時跳出區域最佳解,然後找到更好的解,甚至是全域最佳解之後才凝固,這就是「模擬退火法」的設計原理了。
以下是模擬退火法的演算法的簡要寫法:
Algorithm SimulatedAnnealing(s)
while (溫度還不夠低,或還可以找到比 s 更好的解 s' 的時候)
根據能量差與溫度,用機率的方式決定是否要移動到新解 s'。
將溫度降低一些
end
end 在上述演算法中,所謂的機率的方式,是採用 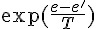 這個機率公式,去判斷是否要從 s 移動到 s',其中 e 是 s 的能量值,而 e' 是 s' 的能量值。
這個機率公式,去判斷是否要從 s 移動到 s',其中 e 是 s 的能量值,而 e' 是 s' 的能量值。
接著,就讓我們來實作一個通用的模擬退火法架構吧 (與前述爬山演算法共用的「解答表示」solution 部份,我們就不再重複貼出了)
通用的模擬退火法架構
檔案:simulatedAnnealing.js
var simulatedAnnealing = function() {} // 模擬退火法的物件模版 (類別)
simulatedAnnealing.prototype.P = function(e, enew, T) { // 模擬退火法的機率函數
if (enew < e)
return 1;
else
return Math.exp((e-enew)/T);
}
simulatedAnnealing.prototype.run = function(s, maxGens) { // 模擬退火法的主要函數
var sbest = s; // sbest:到目前為止的最佳解
var ebest = s.energy(); // ebest:到目前為止的最低能量
var T = 100; // 從 100 度開始降溫
for (var gens=0; gens<maxGens; gens++) { // 迴圈,最多作 maxGens 這麼多代。
var snew = s.neighbor(); // 取得鄰居解
var e = s.energy(); // e : 目前解的能量
var enew = snew.energy(); // enew : 鄰居解的能量
T = T * 0.999; // 每次降低一些溫度
if (this.P(e, enew, T) > Math.random()) { // 根據溫度與能量差擲骰子,若通過
s = snew; // 則移動到新的鄰居解
console.log("%d T=%s %s", gens, T.toFixed(3), s.toString()); // 印出觀察
}
if (enew < ebest) { // 如果新解的能量比最佳解好,則更新最佳解。
sbest = snew;
ebest = enew;
}
}
console.log("solution: %s", sbest.toString()); // 印出最佳解
return sbest; // 傳回最佳解
}
module.exports = simulatedAnnealing; // 將模擬退火演算法的類別匯出。實例:求解平方根
在此,我們將以求解 4 的平方根為例,測試一下上述演算法是否能夠找到正確的解答。
檔案:simulatedAnnealingNumber.js
var simulatedAnnealing = require("./simulatedAnnealing"); // 引入模擬退火法類別
var solutionNumber = require("./solutionNumber"); // 引入平方根解答類別
var sa = new simulatedAnnealing(); // 建立模擬退火法物件
// 執行模擬退火法 (從「解答=0.0」開始尋找, 最多一萬代。
sa.run(new solutionNumber(0.0), 10000);執行結果:
0 T=99.900 energy(-0.010)=4.000
1 T=99.800 energy(0.000)=4.000
...
12 T=98.708 energy(-0.010)=4.000
13 T=98.609 energy(-0.020)=4.000
14 T=98.510 energy(-0.030)=3.999
15 T=98.412 energy(-0.020)=4.000
16 T=98.314 energy(-0.030)=3.999
17 T=98.215 energy(-0.040)=3.998
18 T=98.117 energy(-0.050)=3.998
19 T=98.019 energy(-0.040)=3.998
...
5072 T=0.625 energy(1.250)=2.437
5073 T=0.624 energy(1.240)=2.462
5074 T=0.624 energy(1.230)=2.487
5075 T=0.623 energy(1.240)=2.462
5076 T=0.622 energy(1.250)=2.437
5077 T=0.622 energy(1.260)=2.412
5078 T=0.621 energy(1.270)=2.387
5079 T=0.620 energy(1.280)=2.362
...
6615 T=0.133 energy(1.950)=0.197
6617 T=0.133 energy(1.940)=0.236
6618 T=0.133 energy(1.930)=0.275
6619 T=0.133 energy(1.920)=0.314
6620 T=0.133 energy(1.930)=0.275
6621 T=0.133 energy(1.940)=0.236
6622 T=0.133 energy(1.930)=0.275
...
9377 T=0.008 energy(1.990)=0.040
9378 T=0.008 energy(2.000)=0.000
9396 T=0.008 energy(2.010)=0.040
9397 T=0.008 energy(2.000)=0.000
9528 T=0.007 energy(2.010)=0.040
9531 T=0.007 energy(2.000)=0.000
solution: energy(2.000)=0.000您可以看到上述模擬退火法程式,在一開始的時候幾乎都在亂走,因此浪費了很多時間,但也正是因為這種特性,模擬退火法比較有機會跳脫那些小山谷,而有機會找到更深的山谷,這正式模擬退火法的特性。
雖然花的比較多的時間,但是模擬退火法最後還是正確的找到了 4 的平方根,傳回了 2.000 的結果。
實例:多變數函數的最佳化
在此,我們將以求解 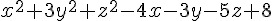 這個函數的最低點,看看上述演算法對多變數函數是否能正常運作。
這個函數的最低點,看看上述演算法對多變數函數是否能正常運作。
檔案:simulatedAnnealingArray.js
var simulatedAnnealing = require("./simulatedAnnealing"); // 引入模擬退火法類別
var solutionArray = require("./solutionArray"); // 引入多變數解答類別 (x^2+3y^2+z^2-4x-3y-5z+8)
var sa = new simulatedAnnealing(); // 建立模擬退火法物件
// 執行模擬退火法 (從「解答(x,y,z)=(1,1,1)」開始尋找, 最多執行 2 萬代。
sa.run(new solutionArray([1,1,1]), 20000);執行結果:
0 T=99.900 energy( 1.000 1.000 0.990 )=1.030
1 T=99.800 energy( 1.000 0.990 0.990 )=1.000
2 T=99.700 energy( 1.000 0.980 0.990 )=0.971
3 T=99.601 energy( 0.990 0.980 0.990 )=0.991
4 T=99.501 energy( 0.990 0.990 0.990 )=1.021
5 T=99.401 energy( 1.000 0.990 0.990 )=1.000
6 T=99.302 energy( 1.000 0.990 1.000 )=0.970
...
5985 T=0.251 energy( 0.870 1.260 1.770 )=0.543
5986 T=0.250 energy( 0.870 1.250 1.770 )=0.497
5987 T=0.250 energy( 0.870 1.250 1.760 )=0.512
5988 T=0.250 energy( 0.870 1.250 1.750 )=0.527
5989 T=0.250 energy( 0.870 1.250 1.760 )=0.512
5990 T=0.249 energy( 0.860 1.250 1.760 )=0.535
...
15036 T=0.000 energy( 2.000 0.500 2.510 )=-3.000
15038 T=0.000 energy( 2.000 0.500 2.500 )=-3.000
15173 T=0.000 energy( 2.010 0.500 2.500 )=-3.000
15174 T=0.000 energy( 2.000 0.500 2.500 )=-3.000
15261 T=0.000 energy( 2.000 0.500 2.490 )=-3.000
15265 T=0.000 energy( 2.000 0.500 2.500 )=-3.000
solution: energy( 2.000 0.500 2.500 )=-3.000您可以看到,上述的模擬退火法程式,總共花了一萬五千多代,終於找到了該多變數函數的谷底,雖然速度不快,但也總算是達成任務了。
結語
當然,模擬退火法雖然比較有機會跳脫小山谷,去找到更深的山谷,但這並不表示模擬退火法一定可以找到最深的山谷。
當溫度已經降到很低的時後,模擬退火法就會逐漸凝固,於是就會固定在某個山谷不出來了。
事實上、沒有任何一種優化方法可以在「多項式時間內」保證找到任何函數的最低點,否則「NP-Complete」問題不就被解掉了,而「NP-Complete」問題事實上在計算理論領域裡,一直還是個最困難的未解之謎啊!
參考文獻
【本文由陳鍾誠取材並修改自 維基百科,採用創作共用的 姓名標示、相同方式分享 授權】
程式人文集
Arduino入門教學(17) – 如何用 Arduino 燒錄 AVR 晶片 (作者:Cooper Maa)
第一部份:用一塊 Arduino 燒錄另一塊 Arduino
這篇教學教你怎麼把 Arduino 板子變成一個 AVR ISP 燒錄器(In-System Programmer),讓我們把它稱作 ArduinoISP。ArduinoISP 允許你用 Arduino 板子把 bootloader 燒錄到 AVR 晶片上,比如 Arduino 板子上所用的 ATmega168 或 ATmega328 晶片。

▲ Arduino Duemilanove w/ ATmega328
什麼是 Bootloader?

▲ AVR ISP
一般來說,要開發 AVR 晶片的程式,除了要有一張 AVR 開發板外,還需要準備一個像上圖一樣稱為 AVR ISP(In-System Programmer) 的特殊的裝置,這種裝置的用途主要是讓開發者可以用它把寫好的韌體上傳到晶片上。

▲ 標準 Arduino 板子上都有 ICSP 排針,AVR ISP 的傳輸線就接在這個位置
什麼是 bootloader 呢?簡單地說,bootloader 是一支程式,晶片上如果有 bootloader,便可以直接把韌體上傳到晶片上,你就不需要 AVR ISP 燒錄裝置了。我們買的 Arduino 板子上的 ATMega 晶片都預先燒錄了 bootloader。市面上也有在賣已經預先燒錄好 Arduino bootloader 的 ATmega 晶片。
平常在用 Arduino IDE 時候,我們既不用準備 AVR ISP,也沒有在 ICSP 介面上接任何連接線,而是直接走 USB 介面就可以上傳程式,之所以可以這麼方便,全都是因為有 bootloader 的關係。
什麼時候需要燒錄 bootloader 呢? 嗯,如果有一天你買了一些材料和全新的 ATmega 晶片,想 DIY 自己做 Arduino 板子的話,那麼就會需要燒錄 bootloader。
材料
- Arduino 板子 x 2
- 單心線 x N
- 全新的 DIP(Dual In-line Package) 包裝 ATmega168 或 ATmega328 晶片
為了方便說明,我們為這兩張 Arduino 板子取個名字,一個是燒錄用的板子,叫作 ArduinoISP,另一個是要被燒錄 bootloader 的板子,稱為 Target board。全新的 ATmega 晶片要放到 Target board 上。
注意:由於 Arduino UNO 目前還未支援,所以你不能把 Arduino UNO 當成 AVR ISP programmer 用。
最好順便準備一個 IC 夾,因為你可能會有需要把 ATmega 晶片從板子上拔起來的時候,使用 IC 夾拔 IC 可以避免接腳受損或折彎。

▲ IC 夾 (圖片來源: 台灣金電子)
Bootloader 燒錄步驟
- 首先,使用 USB cable 連接電腦與 ArduinoISP。啟動 Arduino IDE,點 File > Examples > ArduinoISP 並把程式上傳到 ArduinoISP 板子上。
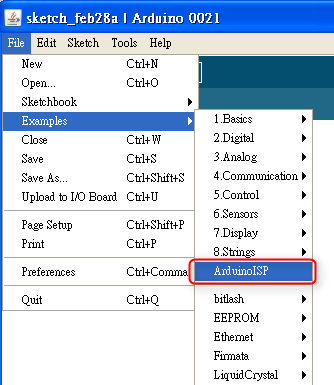
- 照著底下的接線圖把兩張 Arduino 板子接起來:
兩張板子的 pin 11 ~ pin 13 兩兩對接,pin 11 接 pin 11,pin 12 接 pin 12,pin 13 接 pin 13。 兩張板子的 5V 與 Gnd 也是兩兩對接,5V 接 5V,Gnd 接 Gnd。 最後,ArduinoISP 的 pin 10 接到 Target board 的 Reset pin。
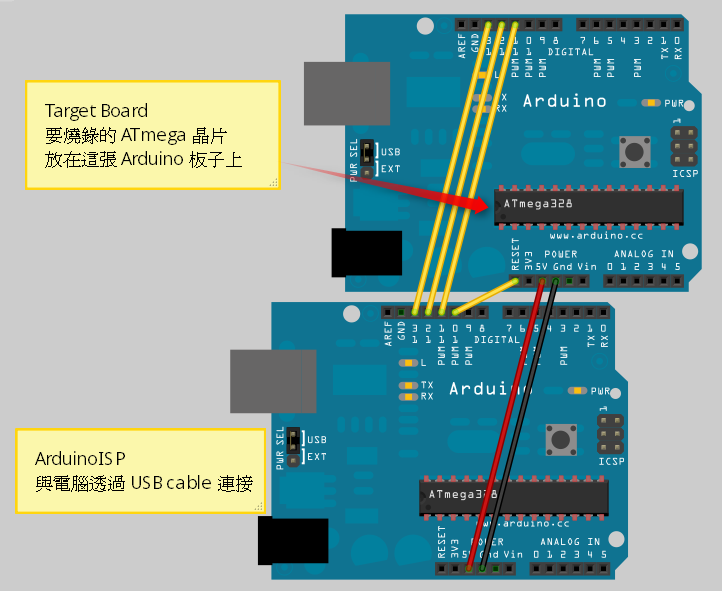
▲ 適用 Arduino Duemilanove 或 Diecimila 的線路接法
Arduino NG 或更早之前的板子因為沒有 reset pin,接法要稍做調整,必須把 ArduiniISP 的 pin 10 接到 Target board 上的 ATmega 晶片的 pin 1:

▲ 適用 Arduino NG 或更早期的板子的線路接法
- 從 Arduino IDE 的 Tools > Board 選單中挑選 Target Board 的 ATMega 晶片要燒錄的 bootloader 版本。
假如你買了一顆全新的 ATMega328 晶片,你想拿這顆晶片來製作 Arduino Duemilanove 相容的板子,那麼在這個地方你就要選擇 "Arduino Duemilanove or Nano w/ ATmega328" 這個選項:
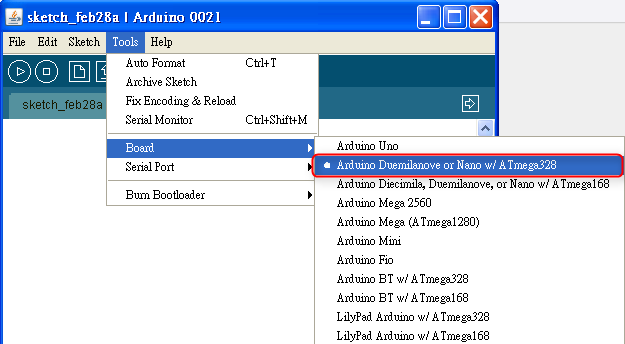
- 點選 Tools > Burn Bootloader > w/ Arduino as ISP 開始燒錄 bootloader。
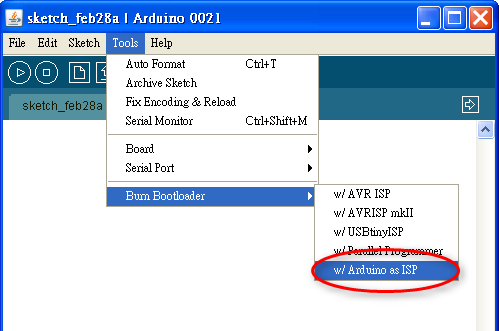
▲ 選 w/ Arduino as ISP
▲ 狀態列訊息: bootloader 燒錄中
▲ 狀態列訊息: bootloader 燒錄完畢
就這樣,當程式上傳完畢後,就完成了 bootloader 的燒錄工作。你可以試試看在 Target Board 上跑個 Blink 程式,看看晶片的運作是否正常。
底下是 bootloader 燒錄動作摘要:
點 File > Examples > ArduinoISP 並把程式上傳到 ArduinoISP 板子上。 照著接線圖連接兩張 Arduino 板子。 從 Tools > Board 選單中挑選 Target Board 的 ATMega 晶片要燒錄的 bootloader 版本。 點 Tools > Burn Bootloader > w/ Arduino as ISP 開始燒錄 bootloader。
第二部份:用一塊 Arduino 燒錄 bootloader 到 AVR 晶片
在第一部份中提到,用 Arduino 做 AVR ISP Programming,我們用了兩張 Arduino 板子,一個是燒錄用的板子,叫作 ArduinoISP,另一個是要被燒錄 bootloader 的板子,稱為 Target board。其實 Target board 不一定非得使用 Arduino 板子不可,你也可以用麵包板當作 Target Board。
用麵包板當作 Target Board 標準版
用麵包板做 Target Board,要準備的材料除了麵包板和 ATmega 晶片外,你還需要 4 個元件:
- 一個 16 MHz 的石英震盪器(Crystal)
- 一個 10k 歐姆電阻,以及
- 兩個 18 到 22 pF(picofarad) 的陶瓷電容
線路接法如下圖:
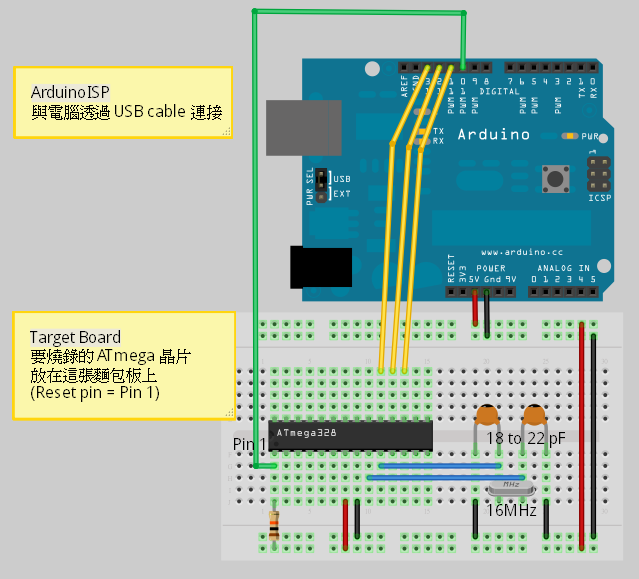
▲ 麵包板當作 Target Board 用,標準版本
用麵包板當作 Target Board 最低需求版
如果你沒有 16 MHz 的石英震盪器也沒有 18-22 pF 的陶瓷電容,那麼你可以設置 ATMega 晶片使用它內部的 8 MHz RC 震盪器當作時脈源。其實 Reset pin 上不放 10K pull up 電阻也沒有關係,所以也可以把它拿掉,這樣你就可以做個最低需求的麵包板 Target Board 了。
線路接法如下圖:
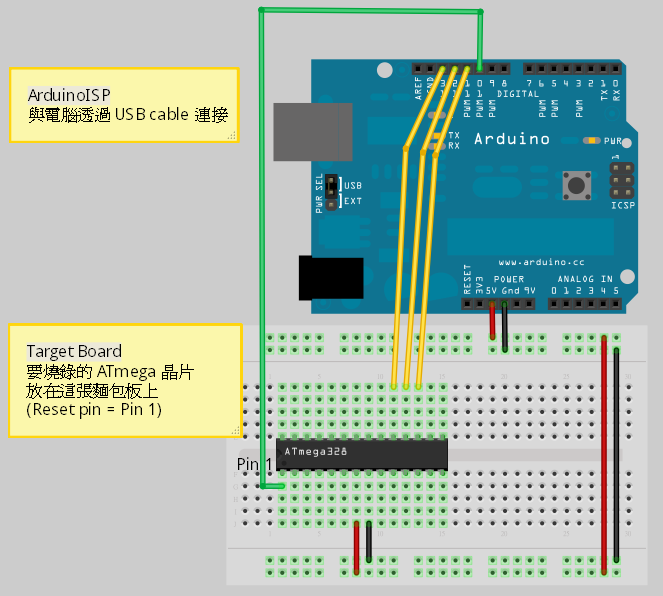
▲ 麵包板當作 Target Board 用,最低需求版本
要用這個最低需求麵包板的 Target Board,你得做一件事。首先打開 C:-00xx.txt (00xx 是你 Arduino IDE 的版本號碼),並將底下這段設定附加到 board.txt 檔案中:
##############################################################
atmega328bb.name=ATmega328 on a breadboard (8 MHz internal clock)
atmega328bb.upload.protocol=stk500
atmega328bb.upload.maximum_size=30720
atmega328bb.upload.speed=57600
atmega328bb.bootloader.low_fuses=0xE2
atmega328bb.bootloader.high_fuses=0xD9
atmega328bb.bootloader.extended_fuses=0x07
atmega328bb.bootloader.path=arduino:atmega
atmega328bb.bootloader.file=ATmegaBOOT_168_pro_8MHz.hex
atmega328bb.bootloader.unlock_bits=0x3F
atmega328bb.bootloader.lock_bits=0x0F
atmega328bb.build.mcu=atmega328p
atmega328bb.build.f_cpu=8000000L
atmega328bb.build.core=arduino:arduino接著重新啟動 Arduino IDE,在 Tools > Board 選單中應該就會看到多了一個 "ATmega328 on a breadboard (8 MHz internal clock)" 的選項:
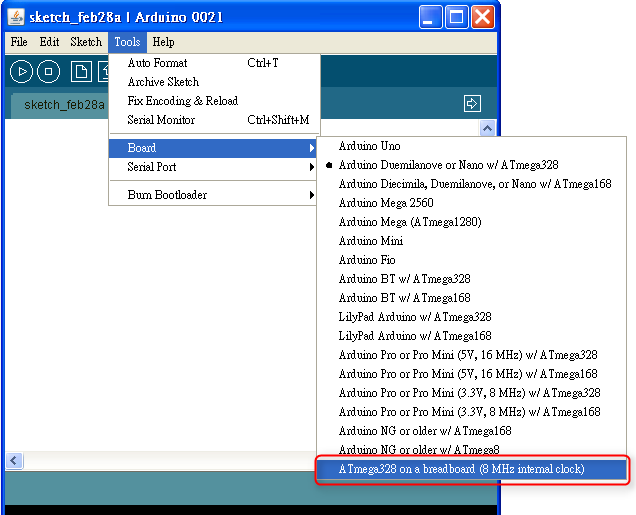
當你設定完成之後,就可以照前一篇的「Bootloader 燒錄步驟」把 bootloader 燒錄到 ATmega 晶片。在燒錄 bootloader 的時候,記得一定要選 "ATmega328 on a breadboard (8 MHz internal clock)" 這個選項,不然的話就沒效。
ATmega328 Pinout
下圖是 ATmega328 晶片的腳位排列圖(Pinout),在連接線路的時候可作為參考:
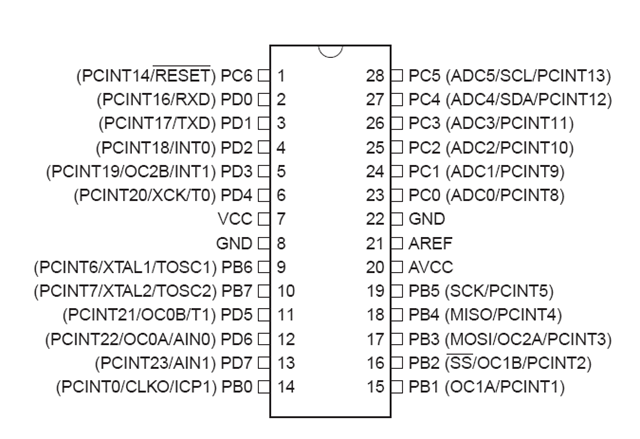
▲ 取自 ATmega328 datasheet
後記
這篇取材自 "From Arduino to a Microcontroller on a Breadboard" 一文,我做過實驗,標準版可以動(加了 16 MHz 石英震盪器的版本),但最低需求版的實驗沒有成功(使用內部 RC 震盪器),在點 Tools > Burn Bootloader > w/ Arduino as ISP 開始燒錄 bootloader 的時候,Arduino IDE 會丟出一個錯誤訊息: "avrdue: Yikes! Invalid device signature.":
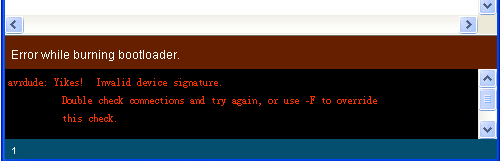
不曉得我哪邊的設定不正確? 我大膽猜測可能是 Fuses 的設定不對,不過 AVR Fues 要怎麼設我不懂,如果有網友試驗成功,還請不吝分享
第三部份:用一塊 Arduino 燒錄程式到 AVR 晶片
在前兩個部分中,我們介紹了 ArduinoISP 而且使用 ArduinoISP 燒錄 bootloader。這次要介紹的是用 ArduinoISP 來燒錄 Arduino 程式(Arduino Sketch)。這種做法是直接把 Arduino Sketch 燒錄到板子上,沒有用到 bootloader,這讓你得以使用 ATmega 晶片全部的程式空間(program space)。所以,原本 ATmega328 的 32 KB 之中有 2 KB 被 bootloader 拿去使用,現在你將可以完整使用這 32 KB 的空間而不再是 30 KB,ATmega168 將是 16 KB 而不再是 14 KB,而 ATmega8 則是 8 KB 而不再是 7 KB。另外,當板子重啟電源時,原本會有 bootloader 的開機延遲 (約 6 至 8 秒),這問題現在也一併避掉了。
使用 ArduinoISP 燒錄 Arduino Sketch
首先,先關掉 Arduino IDE
編輯 Arduino 的 preferences.txt
preferences.txt 可以在這個資料夾中找到:
Mac: /Users/<USERNAME>/Library/Arduino/preferences.txt
Windows: C:\Documents and Settings\<USERNAME>\Application Data\Arduino\preferences.txt
Linux: ~/.arduino/preferences.txt把 upload.using=bootloader 這行改成 upload.using=arduinoisp。
你也可以用其它 ISP,例如 AVR ISP, AVRISP mkII, USBtinyISP 或 Parallel Programmer,這些 ISP 的識別名稱可以在 hardware/programmer.txt 中找到,例如 avrispmkii。
如果只是某張特定的板子需要用 ISP,那麼你可以編輯 hardware.txt,把 <BOARDNAME>.upload.using=<ISPNAME> 這行加到 boards.txt 中。
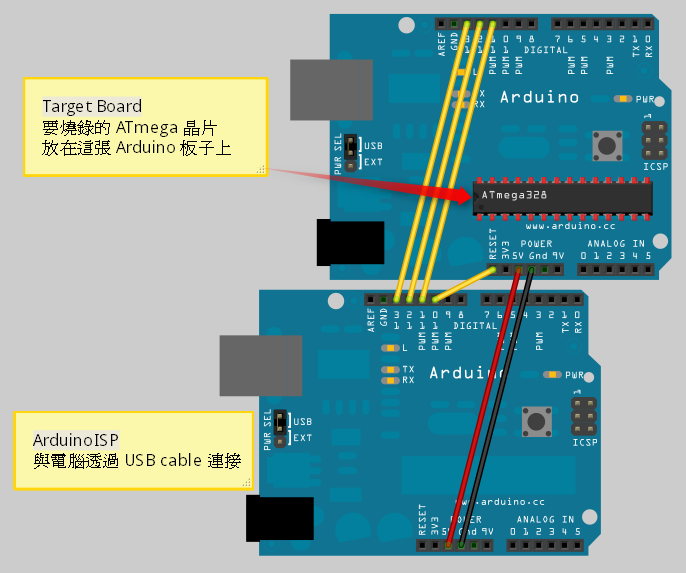
照底下的接線圖把 ArduinoISP 跟 Target Board 連接起來。記得要供電給 Target Board。
接著按照正常的程序,選擇所用的 Arduino 板子,然後按工具列的 Upload 鈕或選單的『File > Upload to I/O board』把 Arduino Sketch 上傳到板子上。
回到正常的 USB/serial 上傳模式
當你不再使用 ISP 燒錄程式時,記得要切換回正常的 USB/serial 上傳模式。你必須把 preferences.txt 的 upload.using 參數還原為 bootloader:
upload.using=bootloader
或是從 boards.txt 中把 <BOARDNAME>.upload.using=<ISPNAME> 這行刪除掉。
記得還得把 bootloader 給燒回 Arduino 板子上。
延伸閱讀
【本文作者為馬萬圳,原文分三篇,網址為: 1. http://coopermaa2nd.blogspot.tw/2011/03/arduino-avr-ispin-system-programmer-1.html , 2. http://coopermaa2nd.blogspot.tw/2011/03/arduino-avr-ispin-system-programmer-2.html, 3. http://coopermaa2nd.blogspot.tw/2011/05/arduino-avr-ispin-system-programmer-3.html ,由陳鍾誠編輯後納入本雜誌】
使用 OpenCV 實作 AR -- 概念篇 (作者: Heresy Ku )
擴增實境(Augmented Reality,簡稱 AR、 維基百科 )這個技術,主要的概念就是把攝影機實際拍到的畫面,在顯示出來的同時,根據畫面的內容,加上其他的資訊、畫面,讓虛擬的物體,可以和真實的廠景融合在一起顯示。
由於把虛擬和現實融合,算是一個相當有趣、而且也相當特別的應用,所以其實在這方面的應用、研究,也都算滿多的;再加上現在許多行動手持裝置,不但配備了小型化的攝影機,也都有足夠的計算能力了,所以在近年來,也算是越來越熱門。不過實際上,這種概念並不算非常地新,在 1994 年就已經有人提出來了~到目前為止,也算是發展好一段時間了。

而雖然 AR 的理想,是可以直接辨識畫面的內容,來做物體的辨識、定位,但是礙於實際上的計算效率、準確性,現階段比較普遍的應用,應該都還是需要特殊哪片、也就是需要「mark」來做辨識、定位的 AR。像上圖,就是一套算是相當成熟的 AR 開放原始碼函式庫、ARToolkit( 官網 、 維基百科 )的示意圖;裡面的人所拿著的,就是專門的 AR 卡片,上面就是即時辨識出這張卡片,並把虛擬人物放進去的效果。
不過,雖然說 ARToolKit 是一個相當成熟的函式庫,但是由於他已經沒有在繼續維護了(News 最後是 2007 年底、提供的 Windows 環境也是到 Visual Studio .Net 2003 而已),所以以現在的觀點來看,在使用上算是有相當地限制…像是他雖然是以 OpenGL 來做 3D 繪圖的函式庫,但是如果要和新的 Shader-based OpenGL 來做整合,似乎也有不少問題。所以當 Heresy 這邊要做 AR 相關的應用的時候,馬上就覺得他並不適和 Heresy 這邊的需求。
而 Heresy 後來使用的,則是使用以 OpenCV( 官網 )這套電腦視覺函式庫所提供的功能為基礎的方法;實作上,主要則是參考 OpenCV-AR( 首頁 )這個 SourceForge 上的開放原始碼專案,來修改而實作完成的。
在這個函式庫的實作裡面,他主要概念,是去偵測畫面中的四邊形、然後把抓到的四邊形影像,轉換成為正方形的圖片,根據指定的樣板進行辨識;如果辨識的相似度夠高,則就視為是要處理的 marker,根據四邊形的四個點來計算出所應對應的矩陣,讓顯示的程式可以透過這個矩陣,來把 3D 的物體畫在對應的位置上。
而由於他是基於四邊形偵測來做處理的,而且辨識的過程又是把影像轉換成正方形,所以它基本上能接受的 marker,就變成一定是要是有明確的四邊形外框的正方形影像了~下面兩張圖,就是這個函式庫所給的兩個範例的 marker:
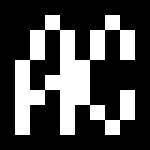
上面兩張圖,基本上是 OpenCV AR 能接受的兩種不同形式的 marker。 左邊的圖基本上是一種比較簡單的形式。他基本上是放大過的圖,原圖大小應該要是 10×10 個像素,每個像素都只有黑或白兩種可能;而由於實際上為了確保外圍的邊還是四邊形,所以外面是不能有白色的;也就是資訊都會記錄在裡面的 8×8、共有 64 個像素的矩形裡。(大小可以透過修改程式來調整) 右邊的則是一個黑底、再加上一般圖片,基本上只要確定黑底在外圍可以構成完整的四邊形、同時影像是方形的,就可以了~而雖然他是給彩色的圖片,不過為了減少環境光造成的影響、同時也減低計算量,所以實際上在內部處理的時候,都是轉換成灰階來做計算的。圖片的大小在程式中並沒有做額外的限制,但是由於圖片越大計算量會越多,所以建議不要用太大的圖檔當作 marker。
前者基本上比較單純,在程式裡面會轉換成編碼過的資料,直接進行比對;基本上不但效率比較好、準確性也比較高;但是相對的,可以變化的幅度就比較小了。
下方是在進行每一個畫面處理時,比較完整的流程圖:
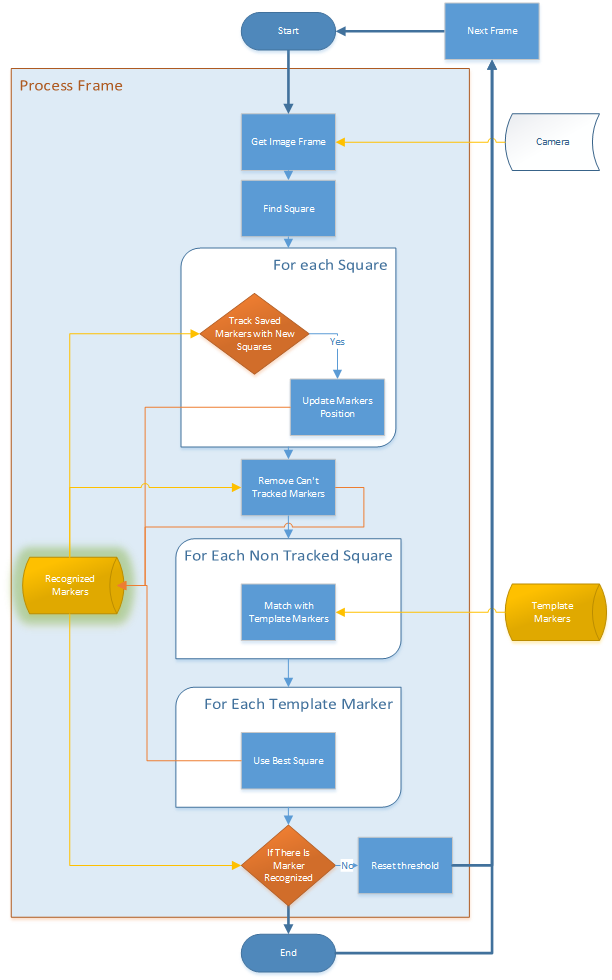
首先,右邊的「Template Markers」是在初始化階段,讀取進來的 marker 的資料,是用來做比對用的樣板(以下稱為 template marker)。而左邊的「Recognized Markers」則是用來記錄成功辨識到的 marker、以及其相對的位置資訊;這個資料在完成後並不會被清除,而是留給外部做存取、以及給下一個畫面做追蹤用的。
在開始後,他會從攝影機取得當下的畫面,做一些處理後,就開始在畫面中偵測四邊形、也就是上圖中「Find Square」的區塊。而在找到畫面中的四邊形後,針對每一個找到的四邊形,會去和之前找到的 marker(Recognized Markers)做比對,如果夠接近的話,就當作是同一個 Marker,然後直接更新它的位置;這基本上算是用追蹤位置的方法,來簡化整個流程的計算量。 而在做完這個動作後,則是會把其他沒有更新過的 Marker 從記錄中刪除,讓 Recognized Markers 裡面只保存在這個畫面,已經追蹤到的 marker。
接下來,則是針對剩下來、沒辦法用 track 來解決的四邊形、則是會把它轉換成正方形的影像後,針對 template markers 裡的所有樣板資料,一筆一筆去做比對,藉此來找出這個四邊形最像的 template marker;這也是整個流程裡面,計算量最大的地方。
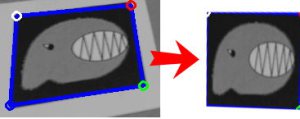
上圖就是這邊的示意圖,左邊的藍色框框,就是找到的四邊形,而強制把他轉換成正方形的影像後,就會像右邊的圖一樣;之後就是透過這個轉換後的影像,來進行比對的。而針對不同類型的 marker,其實也有不同的比對方法,這個就等之後講到這部分再來說了~ 而這樣找出來的結果,可能會有不同的四邊形,都對應到同一個 template marker;而為了避免這樣的問題,這裡則會再去針對每一個 template marker、都去做一次比較,來找出相似度最高的四變形,並以此為最終的結果,存入 Recognized Markers 中。 如果找完後,完全沒有找到四邊形的話,他會去修改進行 binary threshold 時的 threshold 值(他是用亂數產生),來試著讓程式可以在下一個畫面,找到更多四邊形進行測試。 最後,下面就是最後結果的示意圖。左邊是用來偵錯的畫面,裡面的藍色和紅色框框,就是有偵測到的四邊形;由於只是在偵測四邊形,所以可以看到,裡面的手指間,也被認為是一個四邊形了~=而其中藍色是代表有偵測到,但是沒有找到對應的 template marker,而紅色則是有找到對應的,所以可以看到在右邊的結果畫面裡,「Tw」這個 Maker 已經被一個台灣的 3D 物件取代了~

這篇基本上是概念和架構性的文章,大概就先到這邊了。之後有時間,再來寫實作的內容介紹吧~
【本文來自 Heresy's Space 的網誌,原文網址為: http://kheresy.wordpress.com/2012/12/27/ar-by-opencv/ ,由 Heresy 捐出網誌給程式人雜誌,經陳鍾誠編輯後納入雜誌】
亂數產生器 (作者:Bridan)
想過電腦中亂數產生器如何設計的嗎?
大多數亂數產生器採用 線性同餘法 設計 ( Linear Congruential Generator, LCG ),因為方法簡單以及亂數 均勻分佈 ( Uniform distribution )。
其原理為:
Xn = a Xn-1 + b 將一正整數乘以 a 常數再加上 b 常數,
0<= Xn<M 除 M 取餘數,這個 Xn 可重複代入上式計算下一個亂數。各位可以參考 EXCEL 檔 ,我選用 a = 49,b = 0,M = 215 = 32768,C 欄位就是亂數,介於零與一之間,從 E、F 欄位可以看出數值分部非常均勻。 另外,從 A 欄位會發現,每 2048 筆資料會重複循環,這裡所舉的例子是方便讀者明瞭原理,商用軟體至少用32 bits,並挑選合適的 a b 值,所以很難發現重複性。
通常均勻分佈的亂數產生器就夠用,不過與統計有關的程式還需要 常態分佈 ( Normal distribution ) 的亂數產生器,那如何設計呢?還記得 中央極限定理 ( Central limit theorem ) 吧!從未知分佈的母群體中抽樣,只要能計算出這群體平均數 μ 以及有限的變異數 σ2,那麼抽出 n 個隨機樣本取平均值,當 n 趨近無窮大,它的平均值抽樣分配將近似於常態分佈。再以 EXCEL 檔內容為例,一般程式計算時間有限不可能無窮計算下去,因此 只取連續六筆資料平均再正規化 ,原均勻分佈的 C 欄位值,經過計算後就成為 H 欄位常態分佈的亂數,請參考 J 欄位的機率分佈。
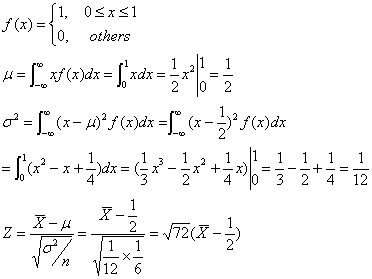
另外,常態分佈亂數方法二,請參考 http://4rdp.blogspot.com/2008/06/random-variable-of-normal-distribution.html 。
(本文來自「研發養成所」 Bridan 的網誌,原文網址為 http://4rdp.blogspot.tw/2008/06/blog-post_14.html ,由陳鍾誠編輯後納入程式人雜誌)
Visual Basic 6.0:奇數魔術方陣(Odd Magic Square) 詳細解法 (作者:廖憲得 0xde)
什麼是奇數魔術方陣 (?)
魔術方陣是許多人想要解決的一個古老的數學問題,您可能在一些雜誌上看過,也可能您的老師有介紹過。一個魔術方陣是在於安排數字在一矩陣[n x n]中,從1到n2, 每一數字僅出現一次, 而且,任一列、任一行或任一對角線的總和都相同。求總和的公式要證明為n [ ( n2 + 1) / 2 ],並不是很困難,若我們利用這個公式,對[5x5]矩陣而言,其總和為5 [ ( 52 + 1 ) / 2 ] = 65,其對應的魔術方陣輸出如下:
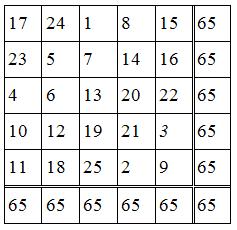
'# [Visual Basic 6.0] 奇數魔術方陣(Odd Magic Square)
'# 0xDe
Dim InputN
Dim Squate()
Private Sub Form_Activate()
'------------------------------
InputN = 3 ' 輸入 (必須為奇數)
'------------------------------
'------------------------------
If InputN Mod 2 = 0 Then Exit Sub ' 判斷是否為奇數
'------------------------------
ReDim Square(InputN - 1, InputN - 1)
'------------------------------
Print "N= " & InputN & "的奇數魔術方陣" & vbCrLf
Randomize Timer ' 亂數產生
TempX = Int(Rnd * InputN) ' 隨機起始 X
TempY = Int(Rnd * InputN) ' 隨機起始 Y
'------------------------------
Do Until N = (InputN ^ 2) ' 直到放滿
If Square(TempX, TempY) = "" Then
N = N + 1
Square(TempX, TempY) = N
TempX = TempX - 1 ' 向上移
If TempX < 0 Then TempX = InputN - 1
TempY = TempY + 1 ' 向右移
If TempY > InputN - 1 Then TempY = 0
Else
' 恢復原本的狀態往下
TempX = TempX + 1
If TempX > InputN - 1 Then TempX = 0
TempY = TempY - 1
If TempY < 0 Then TempY = InputN - 1
' 往下
TempX = TempX + 1
If TempX > InputN - 1 Then TempX = 0
End If
Loop
'------------------------------
For I = 0 To InputN - 1 ' 將結果輸出
For J = 0 To InputN - 1
Print Square(I, J);
Next J
Print
Next I
'------------------------------
End Sub【本文作者為「廖憲得」,原文網址為: http://www.dotblogs.com.tw/0xde/archive/2013/11/13/129187.aspx ,由陳鍾誠編輯後納入本雜誌】
開放電腦計畫 (11) – 中間碼轉組合語言編譯器:使用 node.js + javascript 實作 (作者:陳鍾誠)
前言
在上一期當中我們介紹了 j0c 這個編譯器的設計方式,並且設計了一種稱為 ir0 的中間碼格式,用來做為 j0c 編譯器的輸出格式。
在本文中,我們將介紹一個可以將中間碼 ir0 格式轉換成 CPU0 組合語言 (as0) 的程式,該程式稱為 ir2as0 ,這樣才能接上先前的 as0 組譯器,成為一套完整的工具鏈。
轉換程式
以下是這個轉換程式的原始碼,該程式會將 ir0 格式的中間碼,轉換成 as0 格式的組合語言。
檔案:ir2as.js
// ir2as0 中間碼轉換為組合語言,用法範例: node ir2as0 test.ir0 > test.as0
var fs = require("fs");
var util = require("util");
var format = util.format; // 字串格式化
var log = console.log; // 將 console.log 名稱縮短一點
// 讀入中間檔,並分割成一行一行的字串
var lines = fs.readFileSync(process.argv[2], "utf8").split("\n");
// 輸出組合語言
var asm=function(label, op, p, p1, p2) {
var asCode = format("%s\t%s\t%s\t%s\t%s", label, op, p, p1, p2);
log(asCode);
}
var cmpCount = 0; // 比較運算的標記不可重複,故加上一個 counter 以玆區分
// 將一行中間碼 line 轉換為組合語言
function ir2as(line) {
var tokens = line.split("\t"); // 將中間碼分割成一個一個的欄位
var label = tokens[0]; // 取出標記 label
var iop = tokens[1], aop=""; // 取出運算 iop
var p = tokens.slice(2); // 取出參數部份
if (label !== "") // 若有標記,直接輸出一行只含標記的組合語言
asm(label, "", "", "", "");
switch (iop) { // 根據運算 iop 的內容,決定要轉成甚麼組合語言
case "=": // 範例:= X Y 改為 LD R1, Y; ST R1, X
asm("", "LD", "R1", p[1], "");
asm("", "ST", "R1", p[0], "");
break;
// 範例: + X A B 改為 LD R1, A; LD R2, B; ADD R3, R1, R2; ST R3, X;
case "+": case "-": case "*": case "/": case "<<":
asm("", "LD", "R1", p[1], "");
asm("", "LD", "R2", p[2], "");
aop = {"+":"ADD", "-":"SUB", "*":"MUL", "/":"DIV"}[iop];
asm("", aop, "R3", "R1", "R2");
asm("", "ST", "R3", p[0], "");
break;
// 範例: ++ X 改為 LDI R1, 1; LD R2, X; ADD R2, R1, R2; ST R2, X;
case "++": case "--":
asm("", "LDI", "R1", "1", "");
asm("", "LD", "R2", p[0], "");
aop = {"++":"ADD", "--":"SUB" }[iop];
asm("", aop, "R2", "R1", "R2");
asm("", "ST", "R2", p[0]);
break;
// 範例: < X, A, B 改為 LD R1, A; LD R2, B; CMP R1, R2; JLT CSET0; LDI R1, 1; JMP EXIT0; CSET0: LDI R1, 0; CEXIT0: ST R1, X
case "<": case "<=": case ">": case ">=": case "==": case "!=":
asm("", "LD", "R1", p[1], "");
asm("", "LD", "R2", p[2], "");
asm("", "CMP", "R1", "R2", "");
aop = {"<":"JLT", "<=":"JLE", ">":"JGT", ">=":"JGE", "==":"JEQ", "!=":"JNE"}[iop];
asm("", aop, "CSET"+cmpCounter, "", "");
asm("", "LDI", "R1", "1", "");
asm("", "JMP", "CEXIT"+cmpCounter, "", "");
asm("CSET"+cmpCount, "LDI", "R1", "0", "");
asm("CEXIT"+cmpCount, "ST", "R1", p[0], "");
break;
// 範例: call X, F 改為 CALL F; ST R1, X;
case "call":
asm("", "CALL", p[1], "", "");
asm("", "ST", "R1", p[0], "");
break;
// 範例: arg X 改為 LD R1, X; PUSH R1;
case "arg":
asm("", "LD", "R1", p[0], "");
asm("", "PUSH","R1", "", "");
break;
case "function": // 範例: sum function 只生成標記 sum,沒有生成組合語言指令
break;
case "endf": // 函數結束,沒有生成組合語言指令
break;
case "param": // 範例: param X 改為 POP R1; ST R1, X;
asm("", "POP", "R1", "", "");
asm("", "ST", "R1", p[0], "");
break;
case "return": // 範例: return X 改為 LD R1, X; RET;
asm("", "LD","R1", p[0], "");
asm("", "RET","", "", "");
break;
case "if0": // 範例: if0 X Label 改為 CMP R0, X; JEQ Label;
asm("", "CMP","R0", p[0], "");
asm("", "JEQ",p[1], "", "");
break;
case "goto": // 範例: goto Label 改為 JMP label
asm("", "JMP", p[0], "", "");
break;
case "array": // 範例: X array 改為 LD R1, X; CALL ARRAY; (註: X=new array())
asm("", "LD", "R1", p[0], "");
asm("", "CALL", "ARRAY", "", "");
break;
case "[]": // 範例: [] X A i 改為 LD R1, A; LD R2, i; CALL AGET; ST R1, X (註: X=A[i])
asm("", "LD", "R1", p[1], "");
asm("", "LD", "R2", p[2], "");
asm("", "CALL", "AGET", "", "");
asm("", "ST", "R1", p[0], "");
break;
case "length": // 範例: length len, A 改為 LD R1, A; CALL ALEN; ST R1, len;
asm("", "LD", "R1", p[1], "");
asm("", "CALL", "ALEN", "", "");
asm("", "ST", "R1", p[0], "");
break;
case "apush": // 範例: apush A, X 改為 LD R1,A; LD R2, X; CALL APUSH
asm("", "LD", "R1", p[0], "");
asm("", "LD", "R2", p[1], "");
asm("", "CALL", "APUSH", "", "");
break;
case "table": // 範例: table T 改為 LD R1,T; CALL TABLE
asm("", "LD", "R1", p[0], "");
asm("", "CALL", "TABLE", "", "");
break;
case "map": // 範例: map table field value 改為 LD R1, table; LD R2, field; LD R3, value; CALL TMAP
asm("", "LD", "R1", p[0], "");
asm("", "LD", "R2", p[1], "");
asm("", "LD", "R3", p[2], "");
asm("", "CALL", "TMAP", "", "");
break;
case "":
break;
default:
log("Error : %s not found!", iop);
}
}
// 將所有中間碼都轉換為組合語言
for (var i in lines) {
if (lines[i].trim().length > 0) {
log("// %s", lines[i]);
ir2as(lines[i]);
}
}執行結果
首先我們要使用 j0c 編譯器將 j0 語言的程式,編譯為 ir0 的中間碼格式。然後再利用 ir2as0 將中間碼轉換成 CPU0 的組合語言,以下是一個將 test.j0 編譯 test.ir0 中間檔,然後再利用 ir2as0 將中間檔轉換為 test.as0 組合語言的過程。
C:\Dropbox\Public\web\oc\code\js>node j0c test.j0 > test.ir0
C:\Dropbox\Public\web\oc\code\js>node ir2as0 test.ir0 > test.as0以下是 test.j0 => test.ir0 => test.as0 這個編譯轉換過程當中的檔案內容。
高階語言檔: test.j0
s = sum(10);
function sum(n) {
s = 0;
i=1;
while (i<=10) {
s = s + i;
i++;
}
return s;
}
m = max(3,5);
function max(a, b) {
if (a > b)
return a;
else
return b;
}
function total(a) {
s = 0;
for (i in a) {
s = s + a[i];
}
return s;
}
a = [ 1, 3, 7, 2, 6];
t = total(a);
word = { e:"dog", c:"狗" };中間碼檔案: test.ir0
arg 10
call T1 sum
= s T1
sum function
param n
= s 0
= i 1
L1
<= T2 i 10
if0 T2 L2
+ T3 s i
= s T3
++ i
goto L1
L2
return s
endf
arg 3
arg 5
call T4 max
= m T4
max function
param a
param b
> T5 a b
if0 T5 L3
return a
L3
return b
endf
total function
param a
= s 0
= i 0
L4 length T6 a
< T7 i T6
if0 T7 L5
[] T8 a i
+ T9 s T8
= s T9
goto L4
L5
return s
endf
array T10
apush T10 1
apush T10 3
apush T10 7
apush T10 2
apush T10 6
= a T10
arg a
call T11 total
= t T11
table T12
map T12 e "dog"
map T12 c "狗"
= word T12 組合語言檔: test.as0
// arg 10
LD R1 10
PUSH R1
// call T1 sum
CALL sum
ST R1 T1
// = s T1
LD R1 T1
ST R1 s
// sum function
sum
// param n
POP R1
ST R1 n
// = s 0
LD R1 0
ST R1 s
// = i 1
LD R1 1
ST R1 i
// L1
L1
// <= T2 i 10
LD R1 i
LD R2 10
CMP R1 R2
JLE CSET0
LDI R1 1
JMP CEXIT0
CSET0 LDI R1 0
CEXIT0 ST R1 T2
// if0 T2 L2
CMP R0 T2
JEQ L2
// + T3 s i
LD R1 s
LD R2 i
ADD R3 R1 R2
ST R3 T3
// = s T3
LD R1 T3
ST R1 s
// ++ i
LDI R1 1
LD R2 i
ADD R2 R1 R2
ST R2 i undefined
// goto L1
JMP L1
// L2
L2
// return s
LD R1 s
RET
// endf
// arg 3
LD R1 3
PUSH R1
// arg 5
LD R1 5
PUSH R1
// call T4 max
CALL max
ST R1 T4
// = m T4
LD R1 T4
ST R1 m
// max function
max
// param a
POP R1
ST R1 a
// param b
POP R1
ST R1 b
// > T5 a b
LD R1 a
LD R2 b
CMP R1 R2
JGT CSET0
LDI R1 1
JMP CEXIT0
CSET0 LDI R1 0
CEXIT0 ST R1 T5
// if0 T5 L3
CMP R0 T5
JEQ L3
// return a
LD R1 a
RET
// L3
L3
// return b
LD R1 b
RET
// endf
// total function
total
// param a
POP R1
ST R1 a
// = s 0
LD R1 0
ST R1 s
// = i 0
LD R1 0
ST R1 i
// L4 length T6 a
L4
LD R1 a
CALL ALEN
ST R1 T6
// < T7 i T6
LD R1 i
LD R2 T6
CMP R1 R2
JLT CSET0
LDI R1 1
JMP CEXIT0
CSET0 LDI R1 0
CEXIT0 ST R1 T7
// if0 T7 L5
CMP R0 T7
JEQ L5
// [] T8 a i
LD R1 a
LD R2 i
CALL AGET
ST R1 T8
// + T9 s T8
LD R1 s
LD R2 T8
ADD R3 R1 R2
ST R3 T9
// = s T9
LD R1 T9
ST R1 s
// goto L4
JMP L4
// L5
L5
// return s
LD R1 s
RET
// endf
// array T10
LD R1 T10
CALL ARRAY
// apush T10 1
LD R1 T10
LD R2 1
CALL APUSH
// apush T10 3
LD R1 T10
LD R2 3
CALL APUSH
// apush T10 7
LD R1 T10
LD R2 7
CALL APUSH
// apush T10 2
LD R1 T10
LD R2 2
CALL APUSH
// apush T10 6
LD R1 T10
LD R2 6
CALL APUSH
// = a T10
LD R1 T10
ST R1 a
// arg a
LD R1 a
PUSH R1
// call T11 total
CALL total
ST R1 T11
// = t T11
LD R1 T11
ST R1 t
// table T12
LD R1 T12
CALL TABLE
// map T12 e "dog"
LD R1 T12
LD R2 e
LD R3 "dog"
CALL TMAP
// map T12 c "狗"
LD R1 T12
LD R2 c
LD R3 "狗"
CALL TMAP
// = word T12
LD R1 T12
ST R1 word 結語
截至目前為止,我們已經為開放電腦計畫實作了一組簡單的工具鏈,包含用 node.js + javascript 設計的 j0c 編譯器、ir2as0 中間碼轉換器、 as0 組譯器、vm0 虛擬機、以及用 Verilog 設計的 CPU0, MCU0 處理器等等。
這套工具鏈的設計都是以「簡單易懂」為原則,採用 Keep It Simple and Stupid (KISS) 的原則,希望能透過這樣的方式,揭露電腦的各個設計層面,讓讀者可以透過開放電腦計畫理解電腦從軟體到硬體的設計原理。
不過、我們還沒有完成整個計畫,開放電腦計畫顯然還有些缺憾,像是我們還沒有設計作業系統 (OS),也沒有用 Verilog 設計開放電腦的週邊裝置電路,另外在 FPGA 實際燒錄也只有很簡單的範例程式,還沒辦法形成一套從軟體到硬體串接的很完整的系統。
因此、我們打算在 2014 年暑假在成大與蘇文鈺老師一起舉辦一個「開放FPGA電腦創世紀黑客松」,我們已經為這個活動建立了一個 facebook 社團,歡迎對「開放電腦計畫」或 FPGA 有興趣的朋友們,一起來參與這個活動,以下是該社團的網址:
歡迎大家一同來參加!
Z > b 還是 Z < b (作者:Wush Wu)
最近"Z"和"b"的比較鬧得沸沸揚揚,身為R的重度使用者,當然也要來好好的探討一下這個問題。立馬來試試看:
"Z" > "b"## [1] TRUE沒錯,R語言在這兩者的比較上是支持 Z大於b 的!
作者我呢也對此抱持著堅定不移的信念,直到某天我在linux上使用crontab跑的R程式出現了Bug。
這個Bug非常的隱晦,最困難的地方在於,當我開Rstudio or R console來跑的時候,結果是正確的,但是當我把它丟到crontab下跑的時候,結果卻完全不同。
經過層層追尋之後,我發現問題就在 Z大於b 上啊。在crontab裡, Z小於b !
這是怎麼回事?原來這和locale有關。根據?Comparison的描述:
The collating sequence of locales such as en_US is normally different from C (which should use ASCII) and can be surprising.也就是說,當locale(語系)這個環境變數不同的時候,R在做字母的比較是不同的。當語系設定為如"en_US"或"zh_TW"的時候,大小順序應是: A > B > ... > Z > a > b > ... > z,但是當語系設為"C"的時候,R 會把字元轉成對應的ASCII的整數做比較而此時Z是0x5a,b是0x62,所以Z > b就錯了。
眼就為憑,我們馬上做點實驗:
Sys.setlocale(locale = "zh_TW")## [1] "zh_TW/zh_TW/zh_TW/C/zh_TW/zh_TW.UTF-8""Z" > "b"## [1] TRUESys.setlocale(locale = "C")## [1] "C/C/C/C/C/zh_TW.UTF-8""Z" > "b"## [1] FALSE而一般我們裝R之後,預設會使用如en_US或zh_TW等語系,但是crontab這類環境卻是使用C這個語系。
也因此,我們可以得出結論:
Z大於b不一定是對的,一切都要看你身處的環境啊!
作者 : Wush Wu ()
- Taiwan R User Group Organizer
- R 相關著作:
- 研究領域:Large Scale Learning,Text Mining和Uncertain Time Series
雜誌訊息
讀者訂閱
程式人雜誌是一個結合「開放原始碼與公益捐款活動」的雜誌,簡稱「開放公益雜誌」。開放公益雜誌本著「讀書做善事、寫書做公益」的精神,我們非常歡迎程式人認養專欄、或者捐出您的網誌,如果您願意成為本雜誌的專欄作家,請加入 程式人雜誌社團 一同共襄盛舉。
我們透過發行這本雜誌,希望讓大家可以讀到想讀的書,學到想學的技術,同時也讓寫作的朋友的作品能產生良好價值 – 那就是讓讀者根據雜誌的價值捐款給慈善團體。 讀雜誌做公益也不需要有壓力,您不需要每讀一本就急著去捐款,您可以讀了十本再捐,或者使用固定的月捐款方式,當成是雜誌訂閱費,或者是季捐款、一年捐一次等都 OK ! 甚至是單純當個讀者我們也都很歡迎!
本雜誌每期參考價:NT 50 元,如果您喜歡本雜誌,請將書款捐贈公益團體。例如可捐贈給「羅慧夫顱顏基金會 彰化銀行(009) 帳號:5234-01-41778-800」。(若匯款要加註可用「程式人雜誌」五個字)
投稿須知
給專欄寫作者: 做公益不需要有壓力。如果您願意撰寫專欄,您可以輕鬆的寫,如果當月的稿件出不來,我們會安排其他稿件上場。
給網誌捐贈者: 如果您沒時間寫專欄或投稿,沒關係,只要將您的網誌以 [創作共用的「姓名標示、非商業性、相同方式分享」授權] 並通知我們,我們會自動從中選取需要的文章進行編輯,放入適當的雜誌當中出刊。
給文章投稿者: 程式人雜誌非常歡迎您加入作者的行列,如果您想撰寫任何文章或投稿,請用 markdown 或 LibreOffice 編輯好您的稿件,並於每個月 25 日前投稿到程式人雜誌社團 的檔案區,我們會盡可能將稿件編入隔月1號出版程式人雜誌當中,也歡迎您到社團中與我們一同討論。
如果您要投稿給程式人雜誌,我們最希望的格式是採用 markdown 的格式撰寫,然後將所有檔按壓縮為 zip 上傳到社團檔案區給我們, 如您想學習 markdown 的撰寫出版方式,可以參考 看影片學 markdown 編輯出版流程 一文。
如果您無法採用 markdown 的方式撰寫,也可以直接給我們您的稿件,像是 MS. Word 的 doc 檔或 LibreOffice 的 odt 檔都可以,我們 會將這些稿件改寫為 markdown 之後編入雜誌當中。
參與編輯
您也可以擔任程式人雜誌的編輯,甚至創造一個全新的公益雜誌,我們誠摯的邀請您加入「開放公益出版」的行列,如果您想擔任編輯或創造新雜誌,也歡迎到 程式人雜誌社團 來與我們討論相關事宜。
公益資訊
| 公益團體 | 聯絡資訊 | 服務對象 | 捐款帳號 |
|---|---|---|---|
| 財團法人羅慧夫顱顏基金會 | http://www.nncf.org/ 02-27190408分機 232 |
顱顏患者 (如唇顎裂、小耳症或其他罕見顱顏缺陷) | 銀行:009彰化銀行民生分行 帳號:5234-01-41778-800 |
| 社團法人台灣省兒童少年成長協會 | http://www.cyga.org/ 04-23058005 |
單親、隔代教養.弱勢及一般家庭之兒童青少年 | 銀行:新光銀行 戶名:台灣省兒童少年成長協會 帳號:103-0912-10-000212-0 |