從爬山演算法到梯度下降法
爬山演算法 (Hill Climbing) 是一種最簡單的優化算法,該方法就像模擬人類爬山時的行為而設計的,因此稱為爬山演算法。
程式究竟要怎麼爬山呢?且讓我們用一張圖來看看。
假如我們在 Google 裏輸入一個算式,Google 會幫我們畫出該函數。舉例而言,如果我在 Google 輸入 x^2+3x+5 這個算式,您會看到下列圖形:
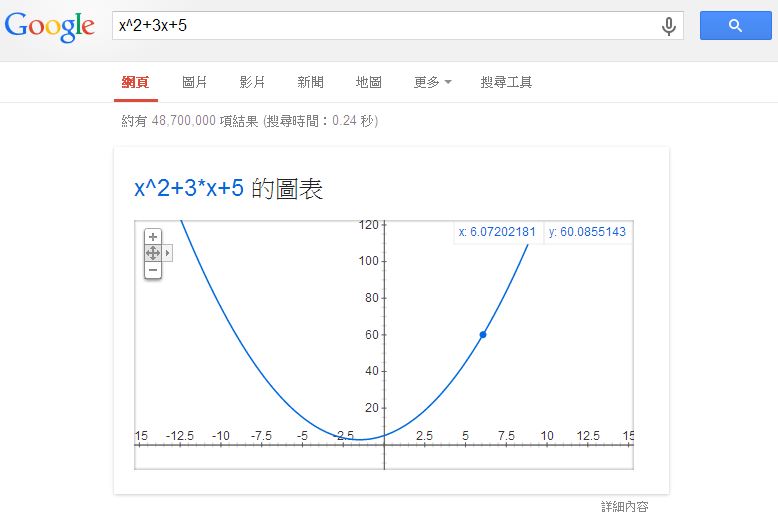
圖、在 Google 輸入 x^2+3x+5 後顯示的函數圖
這時您可以移動滑鼠,圖形會出現一個可移動的小藍點,該點會沿著曲線移動,上圖中 (x, y) 座標顯示為 x:6.07202181, y:60.0855143, 就是那個小藍點所在的位置。
如果我們想要寫程式尋找這個函數的最低點,那我們應該怎麼找呢?
其實方法很簡單,就是一直往低的地方走,一直走到最低點,然後你會看到左右兩邊都沒辦法更低了,於是就停止尋找,傳回該最低點作為答案。
這個方法,就像是水往低處流一樣,不斷的往更低的方向流,最後一定會流到一個山谷,然後就積成一個湖了。
但是、既然這樣,那為甚麼叫做爬山演算法,而不叫「流水下山演算法」呢?
其實、只要反過來看就行了,如果我們想要找的是最高點,而不是最低點,那整個行為就會像爬山一樣,只是最後爬到山頂就會停了。
採用這種想法,若我們想找 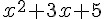 這個函數的最高,我們可以在 Google 輸入
這個函數的最高,我們可以在 Google 輸入 -(x^2+3x+5) 就可以看到那座山了,以下是 Google 顯示的結果:
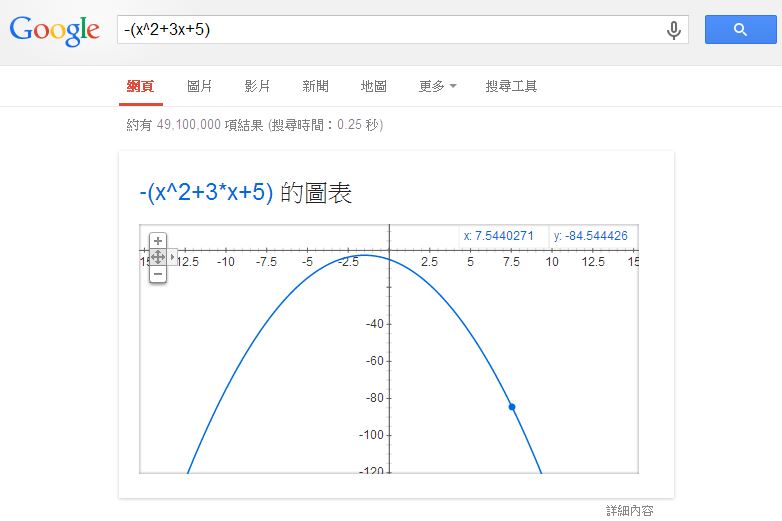
圖、在 Google 輸入 -(x^2+3x+5) 後顯示的函數圖
當然、如果函數有很多山峰,那這種方法只能走到小山丘就會停了。這時您可能會說,那為甚麼不再繼續往更高的山走去呢?
關於這點,並不是不行,只是程式沒有眼睛,也沒辦法一眼望去把所有的地形都給看光,然後知道更高的山峰在哪裡?
如果我們用上面水往低處流的想法,您就會清楚爬山演算法所遭遇的困難了。當您像水一樣往下流,到了谷底之後,由於四周都是山壁,所以您根本看不到更低的谷到底在哪裡,所以只好就停下來了。
此時、除非你爬出山谷,否則根本不可能找到更深的谷,這就是「流水下山演算法」所遭遇到的困難了。以下是我們用 Google 顯示 (x-5)*(x-3)*(2x+5)*(x+3) 這個具有兩個山谷的函數,所得到的圖形。
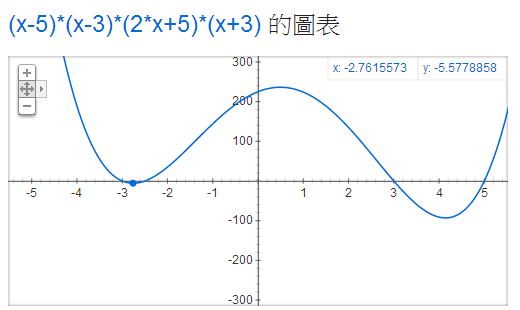
圖、兩個山谷的情況,如何找到最低的山谷呢?
假如我們在上圖中左邊的山谷,那麼怎麼能知道右邊還有一個更低的山谷呢?這就是「流水下山演算法」的困難之所在了!
當然、也有人試圖提出一些企圖找到更深的谷,或爬到更高的山的演算法,這些演算法往往是以爬山演算法為基礎,然後再作一些改良,像是「模擬退火演算法」(Simulated Annealing Algorithm) 或大洪水演算法 (Great Deluge algorithm) 等等,這些方法都是企圖讓「流水下山演算法」有機會跳出山谷而設計的方法。
當然、您也可以企圖加上「衝力」之類的想法讓「流水下山演算法」可以衝出低谷,但是到底要衝多久,還有該往哪個方向衝才對呢?那這種方法是否該改叫「衝山演算法」呢?
當然、我是沒有聽過這種名稱啦!
另外、對於上述的單變數函數而言,不是往左邊走就是往右邊走,但是如果有兩個變數,例如像 x^2+y^2+3x+5y+6 ,但是只有一個山谷,那麼我們該修改哪個變數呢?舉例而言,以下就是 Google 所畫出的 x^2+y^2+3x+5y+6 之圖形。
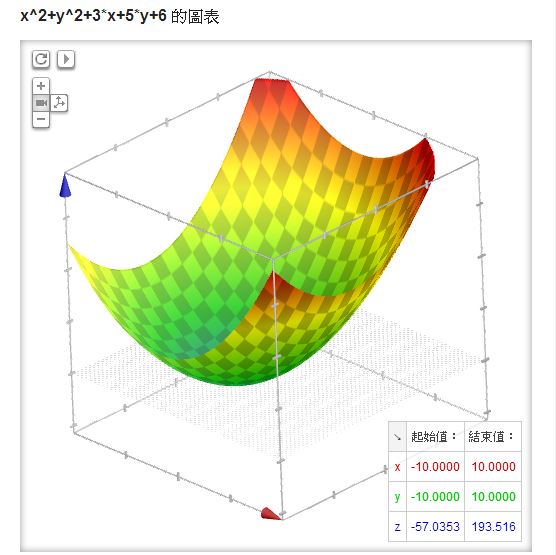
在上述的雙變數情形中,我們可以隨機的挑一個變數,然後向左或向右移動一小步,只要移動後的點更低就接受,如果連續很多次移動都沒辦法找到更低的點,就認為已經到達山谷,這樣的方法其實還蠻有效的,這種方法可以稱為「隨機下山演算法」 (反過來英文中以爬山的角度來看,所以稱為隨機爬山演算法 Stochastic Hill Climbing Algorithm)。
當然、隨機的方法有時會比較沒效率,如果我們可以很容易的透過微積分計算斜率 (導數) 的話,那麼不管幾個變數,我們都可以計算出山坡上最陡峭的那一個方向,這種微積分概念稱為「梯度」,如下圖所示:
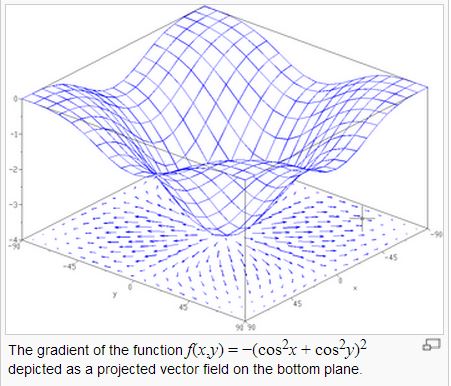
圖、曲面與每一點的梯度向量
在上圖中,底下的平面上所畫的向量,就是上面那個曲面在該點的梯度,換句話說某一點的梯度其實是一個向量。梯度的計算公式如下:
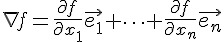
如果我們可以計算某函數之梯度的話,那麼就可以不用透過隨機的方式去亂走了,只要朝著梯度的方向走去,就是最快下降的道路了。
如果我們採用這種沿著梯度方向往下走的方法,就稱為「梯度下降法」(Gradient Descent),這種方法可以說是一種「貪婪演算法」(Greedy Algorithm),因為它每次都朝著最斜的方向走去,企圖得到最大的下降幅度。
在程式人雜誌上一期的焦點「神經網路」中的「反傳遞演算法」,其實就是一種梯度下降法,所以才會有下列這段程式:
function sigmoid(x) {
return ml.tanh(x);
}
function dsigmoid(y) {
return 1.0 - y*y;
}其中的 sigmoid(x) 設定為 tanh(x) 這個函數,tanh(x) 的數學定義如下:
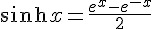
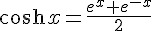
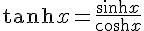
而 dsigmoid(y) 中的 1.0 - y*y 則是 y=tanh(x) 的微分式,對每個 y=tanh(x) 都取微分式的時候,其實就是梯度的方向,因此「反傳遞演算法」事實上是一種梯度下降法啊!
這時,或許各位會想起,「貪婪演算法」怎麼感覺有點熟悉,似乎在哪裡學過?
如果各位學過演算法課程,或許想起像「最小擴展樹」(Minimal Spanning Tree) 的演算法,您會想到這種方法也很貪婪,因為每次都找最小的邊來加入,那也是一種「貪婪演算法」,但這與此處的貪婪演算法之概念顯然有些差距了。
參考文獻
- Wikipedia:Hill climbing
- Wikipedia:Great Deluge algorithm
- Wikipedia:Simulated annealing
- Wikipedia:Stochastic hill climbing
- Wikipedia:Gradient descent
- Wikipedia:Greedy algorithm
- 維基百科:爬山演算法
- 維基百科:模擬退火
- 維基百科:梯度下降法
- 維基百科:貪心法
【本文由陳鍾誠取材並修改自 維基百科,採用創作共用的 姓名標示、相同方式分享 授權】