前言
編輯小語
在本期的「程式人雜誌」中，聚焦的主題是「電腦下棋」，除了探討電腦下棋的歷史、Min-Max 對局搜尋法與 Alpha-Beta Cut 等修剪法等理論之外，我們還設計了一個只採用盤面評估函數，沒有採用任何搜尋法的五子棋實作，希望能以程式人的角度清楚的說明「電腦下棋」程式的原理。
在程式與科學裏，我們對最近網路上一則宣稱「圖靈測試」已經被通過的訊息，進行了深入的探討。透過這個探討，也能順便理解「不正確的科學傳播」是如何造成的，並且回顧一下何謂圖靈測試。
另外、還有 Arduino, GoogleMap API, 對數的電腦計算方法等，還有在「開放電腦計畫」中我們採用「硬體導向」的方式重新設計了 MCU0 微控制器的迷你版等內容，希望您會喜歡這期的「程式人雜誌」！
---- （程式人雜誌編輯 - 陳鍾誠）
授權聲明
本雜誌許多資料修改自維基百科，採用 創作共用：姓名標示、相同方式分享 授權，若您想要修改本書產生衍生著作時，至少應該遵守下列授權條件：
- 標示原作者姓名 (包含該文章作者，若有來自維基百科的部份也請一併標示)。
- 採用 創作共用：姓名標示、相同方式分享 的方式公開衍生著作。
另外、當本雜誌中有文章或素材並非採用 姓名標示、相同方式分享 時，將會在該文章或素材後面標示其授權，此時該文章將以該標示的方式授權釋出，請修改者注意這些授權標示，以避免產生侵權糾紛。
例如有些文章可能不希望被作為「商業性使用」，此時就可能會採用創作共用：姓名標示、非商業性、相同方式分享 的授權，此時您就不應當將該文章用於商業用途上。
最後、懇請勿移除公益捐贈的相關描述，以便讓愛心得以持續散播！
本期焦點
電腦下棋簡介
自從有了電腦之後，人們就一直想讓電腦「學會」下棋的能力。事實上、遠在 1952 年，那時的電腦雖然還不具備下棋的能力，但是資訊領域的理論派大師圖靈 (Alan Turing) 就已經在構思如何寫「電腦下棋」的程式了，以下是節錄自維基百科的一段描述：
1952年，圖靈寫了一個西洋棋程式。可是，當時沒有一台電腦有足夠的運算能力去執行這個程式，他就模仿電腦，每走一步要用半小時。他與一位同事下了一盤，結果程式輸了。
後來美國新墨西哥州洛斯阿拉莫斯國家實驗室的研究群根據圖靈的理論，在ENIAC上設計出世界上第一個電腦程式的象棋－洛斯阿拉莫斯象棋。
世界上有很多種棋類遊戲，對於台灣人而言，最常下的幾種棋類，大至上包含「圍棋、象棋、五子棋、西洋棋」等等。
圍棋的英文名稱為 GO，起源於中國，推測起源時間為大約公元前6世紀。傳說堯的兒子丹朱頑劣，堯發明圍棋以教育丹朱，陶冶其性情。目前圍棋的最早可靠記載見於春秋時期的《左傳》，戰國時期的弈秋是見於史籍的第一位棋手，最早的圍棋文物可以追溯到戰國時期。漢朝時棋盤為17路，南北朝時候，棋盤定型為現在的19道棋盤，傳入朝鮮半島，並且出現了評定棋手水平的圍棋九品制。圍棋逐漸成為中國古代知識階層修身養性的一項必修課目，為「琴棋書畫」四藝之一。
圍棋在公元7世紀傳入日本，很快就流行於宮廷和貴族之中。戰國末期，豐臣秀吉設立棋所。德川幕府時代，出現了在天皇或將軍面前對弈的「御城棋」，日本圍棋逐漸興盛，出現了本因坊、安井、井上、林等圍棋世家。其中坊門尤其人才輩出，先後出現了道策、丈和、秀和、秀策、秀甫、秀榮等傑出棋士。日本圍棋由於廢除了中國古代圍棋的座子制（古代中國圍棋是放四個座子，就是兩黑兩白放在對角星的位置上，雙方在這個基礎上開始布局），布局理論得以極大發展。
明治維新以後，棋手失去幕府支援，開始謀求新的謀生手段，導致了新聞棋戰和現代段位制的出現，並創立了全國性的日本棋院。昭和時代，吳清源和木谷實共同掀起了「新布局」的潮流，開始了現代圍棋的時代。其後日本棋界一流棋手輩出，如坂田榮男，藤澤秀行，高川格，及後來的大竹英雄，武宮正樹，小林光一，石田芳夫等。
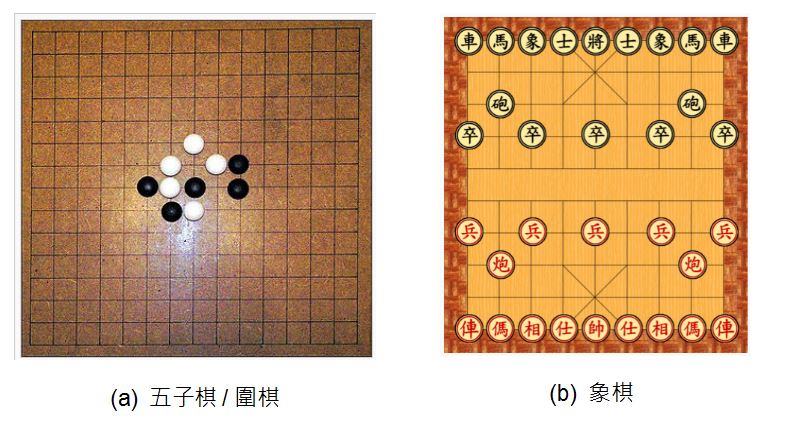
五子棋的英文名稱為 GOMOKU，在日本平安時代就有，是日本人頗受歡迎的棋類。自1899年日本棋士黒岩涙香證明了原始規則的五子棋先下必勝後，五子棋邁入一條不斷改良的道路，經過數十年的修改、驗證、再修改，最終發展出加入禁手的五子棋，並經過公開徵名，稱為連珠（RENJU），因此規則在日本成型，又稱為日式規則或連珠規則。
西洋棋的英文就是 chess，又稱歐洲象棋或國際象棋，一般被認爲源自一種印度的遊戲——恰圖蘭卡，7世紀時流傳至波斯成為波斯象棋。穆斯林統治波斯後，它被帶到伊斯蘭的國家。九世紀傳入南歐，10世紀時傳到西班牙，11世紀傳到英國。15世紀末，現代西洋棋的規則逐漸成形。現代的玩法與19世紀時的大致相同。由於流傳已久，因此在各地與各時期產生不少的西洋棋變體規則。
相信大部分的人對以上棋類都相當熟悉，也都知曉這些棋類的遊戲規則了，現在、就讓我們大致介紹一下如何撰寫「電腦下棋」的程式好了。
要寫下棋程式，大致有三個關鍵技巧，第一個是盤面的表達，第二個是評估函數，第三個是搜尋技巧。
- 盤面表達：通常我們可以用一個陣列代表盤面。舉例而言、在支援 Unicode 的系統中，我們可以用字元陣列代表棋盤，對於圍棋或五子棋而言，我們可以用 O 代表白子、 X 代表黑子，然後用空白字元代表該位置還沒有任何子。同樣的、我們可以用中文字的「將士象車馬砲卒」與「帥仕相俥傌炮兵」來代表象棋的子，對於西洋棋也可以如法炮製，只要對每個棋子都取一個中文名字或代號就行了。
- 評估函數：接著我們可以寫一個函數來評估某個盤面的分數，舉例而言、對於五子棋而言，我方連五子得 100 分，對方連五子則扣 100 分，我方連四子得 30 分，對方連四子則扣 30 分， ......，我方連兩子得 2 分，對方連兩子則扣兩分。而對象棋而言，則可以對每一子的重要性計分，例如將算 100 分，車算 50 分，砲算 30 分等等。
- 搜尋策略：對於比較複雜的棋類，我們通常需要事先設想後面好幾步的情況，能夠想得越周全且越遠的人，通常就會越厲害。電腦下棋也是如此，由於現在電腦的速度非常快，因此往往可以利用 Min-Max 演算法搜尋兩三層，甚至到五六層。而且、只要加上 Alpha-Beta Cut 修剪法，有時甚至可以搜尋到十幾層，這樣的能力往往可以超過人類，因此現在電腦在「象棋、西洋棋、五子棋」上的棋力通常很強，即使職業的棋手也未必能夠打贏電腦。(不過圍棋目前還是人類較強，電腦還沒辦法下贏職業棋手)。
在 1997 年的時候，IBM 曾經用他的「深藍」(Deep Blue) 電腦與當時的世界西洋棋王「卡斯巴羅夫」公開對戰，結果「卡斯巴羅夫」在第一盤勝利之後，卻連續輸了兩盤，於是敗給了「深藍電腦」。雖然這場棋賽引起了一些爭議，但是電腦在西洋棋上的棋力，應該已經確定不亞於職業棋手，甚至是有過之而無不及了。
我們將在以下的幾篇文章中，進一步討論電腦下棋的方法，並且實作出一個「五子棋」的「電腦自動下棋」程式。
參考文獻
- Wikipedia:Computer chess
- 維基百科:電腦象棋
- Wikipedia:Deep Blue
- 維基百科:深藍
- 維基百科:西洋棋
- 維基百科:圍棋
- http://chessprogramming.wikispaces.com/Learning
【本文由陳鍾誠取材並修改自 維基百科，採用創作共用的 姓名標示、相同方式分享 授權】
五子棋程式 -- 以 JavaScript+Node.js 實作 (作者：陳鍾誠)
簡介
在本文中，我們設計了一個完全只是依賴「盤面評估函數」的五子棋程式，這個程式並沒有採用「Min-Max 對局搜尋法」，更沒有採用「Alpha-Beta 修剪法」，但是已經能夠與一般人對戰，有時候還可以贏得棋局。
以下是這個程式執行的一個畫面，我們採用命令列的設計方式，使用者下子時必須輸入格子的座標，該座標由兩個 16 進位字母組成，例如圖中的 62 代表下在第六列第二行的位置。
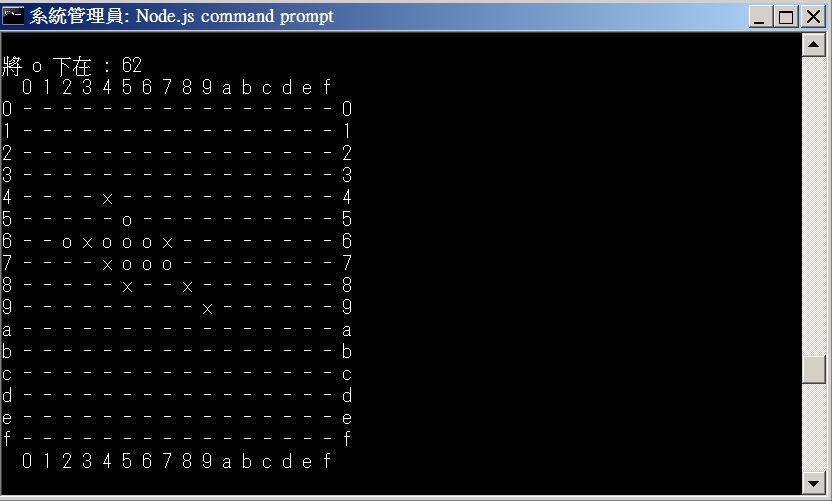
圖、五子棋程式的一個對局畫面
程式實作
整個程式的實作只包含以下這個 chess.js 檔案，完整原始碼如下。
檔案：chess.js
// 五子棋遊戲，單機命令列版
// 人對人下：node chess P2P
// 人對電腦：node chess P2C
// 作者：陳鍾誠
var util = require("util");
var log = console.log;
var r = require('readline').createInterface(process.stdin, process.stdout);
// 印出訊息，並取得輸入。
var prompt = function(turn) {
var msg = format('將 %s 下在 : ', turn);
r.setPrompt(msg);
r.prompt();
}
var format = function() { // 字串格式化
return util.format.apply(null, arguments);
}
// 棋盤物件
var Board = function() {
this.m = [];
for (var r=0; r<16; r++) {
this.m[r] = [];
for (var c=0; c<16; c++)
this.m[r][c] = '-';
}
}
// 將棋盤格式化成字串
Board.prototype.toString = function() {
var str = " 0 1 2 3 4 5 6 7 8 9 a b c d e f\n";
for (var r=0; r<16; r++) {
str += r.toString(16)+" "+this.m[r].join(" ")+" "+r.toString(16)+"\n";
}
str += " 0 1 2 3 4 5 6 7 8 9 a b c d e f\n";
return str;
}
// 顯示棋盤
Board.prototype.show = function() {
log(this.toString());
}
// 以下為遊戲相關資料與函數
// var zero = [ 0, 0, 0, 0, 0];
// var inc = [-2,-1, 0, 1, 2];
// var dec = [ 2, 1, 0,-1,-2];
var z9 = [ 0, 0, 0, 0, 0, 0, 0, 0, 0];
var i9 = [-4,-3,-2,-1, 0, 1, 2, 3, 4];
var d9 = [ 4, 3, 2, 1, 0,-1,-2,-3,-4];
var z5 = [ 0, 0, 0, 0, 0];
var i2 = i9.slice(2,-2);
var d2 = d9.slice(2,-2);
// 檢查在 (r, c) 這一格，規則樣式 (dr, dc) 是否被滿足
// dr, dc 的組合可用來代表「垂直 | , 水平 - , 下斜 \ , 上斜 /」。
var patternCheck=function(board, turn, r, c, dr, dc) {
for (var i = 0; i < dr.length; i++) {
var tr = Math.round(r+dr[i]);
var tc = Math.round(c+dc[i]);
if (tr<0 ||tr > 15 || tc<0 || tc>15)
return false;
var v = board.m[tr][tc];
if (v != turn) return false;
}
return true;
}
// 檢查是否下 turn 這個子的人贏了。
var winCheck = function(board, turn) {
var win = false;
for (var r=0; r<16; r++) {
for (var c=0; c<16; c++) {
if (patternCheck(board, turn, r, c, z5, i2)) // 垂直 | ;
win = true;
if (patternCheck(board, turn, r, c, i2, z5)) // 水平 - ;
win = true;
if (patternCheck(board, turn, r, c, i2, i2)) // 下斜 \ ;
win = true;
if (patternCheck(board, turn, r, c, i2, d2)) // 上斜 / ;
win = true;
}
}
if (win) {
log("%s 贏了！", turn); // 如果贏了就印出贏了
process.exit(0); // 然後離開。
}
return win;
}
var peopleTurn = function(board, turn, line) {
var r = parseInt(line[0], 16); // 取得下子的列 r (row)
var c = parseInt(line[1], 16); // 取得下子的行 c (column)
if (r<0 || r>15 || c<0 || c>15) // 檢查是否超出範圍
throw "(row, col) 超出範圍!"; // 若超出範圍就丟出例外，下一輪重新輸入。
if (board.m[r][c] != '-') // 檢查該位置是否已被佔據
throw format("(%s%s) 已經被佔領了!", line[0], line[1]); // 若被佔據就丟出例外，下一輪重新輸入。
board.m[r][c] = turn; // 否則、將子下在使用者輸入的 (r,c) 位置
}
var P2P=function(b, turn, line) {
peopleTurn(b, turn, line);
b.show(); // 顯示棋盤現況
winCheck(b, turn);
return (turn == 'o')?'x':'o'; // 換對方下了。
}
var attackScores = [ 0, 3, 10, 30, 100, 500 ];
var guardScores = [ 0, 2, 9, 25, 90, 400 ];
var attack=1, guard=2;
var getScore = function(board, r, c, turn, mode) {
var score = 0;
var mScores = (mode === attack)?attackScores:guardScores;
board.m[r][c] = turn;
for (var start = 0; start <= 4; start++) {
for (var len = 5; len >= 1; len--) {
var end = start+len;
var zero = z9.slice(start, start+len);
var inc = i9.slice(start, start+len);
var dec = d9.slice(start, start+len);
if (patternCheck(board, turn, r, c, zero, inc)) // 攻擊：垂直 | ;
score += mScores[len];
if (patternCheck(board, turn, r, c, inc, zero)) // 攻擊：水平 - ;
score += mScores[len];
if (patternCheck(board, turn, r, c, inc, inc)) // 攻擊：下斜 \ ;
score += mScores[len];
if (patternCheck(board, turn, r, c, inc, dec)) // 攻擊：上斜 / ;
score += mScores[len];
}
}
board.m[r][c] = '-';
return score;
}
var computerTurn = function(board, turn) {
var best = { r:0, c:0, score:-1 };
for (var r=0; r<=15; r++) {
for (var c=0; c<=15; c++) {
if (board.m[r][c] !== '-')
continue;
var attackScore = getScore(board, r, c, 'x', attack); // 攻擊分數
var guardScore = getScore(board, r, c, 'o', guard); // 防守分數
var score = attackScore+guardScore;
if (score > best.score) {
best.r = r;
best.c = c;
best.score = score;
}
}
}
log("best=%j", best);
board.m[best.r][best.c] = turn; // 否則、將子下在使用者輸入的 (r,c) 位置
}
var P2C=function(b, turn, line) {
peopleTurn(b, 'o', line);
b.show(); // 顯示棋盤現況
winCheck(b, 'o'); // 檢查下了這子之後是否贏了！
computerTurn(b, 'x', line);
b.show();
winCheck(b, 'x');
return 'o';
}
var chess=function(doLine) {
// 主程式開始
var b = new Board(); // 建立棋盤
b.show(); // 顯示棋盤
var turn = 'o'; // o 先下
prompt(turn); // 提示要求下子訊息，並接受輸入。
r.on('line', function(line) { // 每當讀到一個字串時。
try {
turn = doLine(b, turn, line);
} catch (err) { // 若有丟出例外
log(err); // 則印出錯誤訊息。
}
prompt(turn); // 提示要求下子訊息，並接受輸入。
}).on('close', function() { // 輸入結束了
process.exit(0); // 程式結束。
});
}
if (process.argv[2] === "P2P") // 人對人下
chess(P2P);
else if (process.argv[2] === "P2C") // 人對電腦下
chess(P2C);
else { // 命令下錯，提示訊息！
log("人對人下：node chess P2P\n人對電腦：node chess P2C");
process.exit(0);
}執行結果
以下是一場對局的過程片段，您可以看到最後是 x 贏了，也就是人類贏了。
C:\Dropbox\Public\web\ai\code\chess>node chess P2C
0 1 2 3 4 5 6 7 8 9 a b c d e f
0 - - - - - - - - - - - - - - - - 0
1 - - - - - - - - - - - - - - - - 1
2 - - - - - - - - - - - - - - - - 2
3 - - - - - - - - - - - - - - - - 3
4 - - - - - - - - - - - - - - - - 4
5 - - - - - - - - - - - - - - - - 5
6 - - - - - - - - - - - - - - - - 6
7 - - - - - - - - - - - - - - - - 7
8 - - - - - - - - - - - - - - - - 8
9 - - - - - - - - - - - - - - - - 9
a - - - - - - - - - - - - - - - - a
b - - - - - - - - - - - - - - - - b
c - - - - - - - - - - - - - - - - c
d - - - - - - - - - - - - - - - - d
e - - - - - - - - - - - - - - - - e
f - - - - - - - - - - - - - - - - f
0 1 2 3 4 5 6 7 8 9 a b c d e f
將 o 下在 : 66
0 1 2 3 4 5 6 7 8 9 a b c d e f
0 - - - - - - - - - - - - - - - - 0
1 - - - - - - - - - - - - - - - - 1
2 - - - - - - - - - - - - - - - - 2
3 - - - - - - - - - - - - - - - - 3
4 - - - - - - - - - - - - - - - - 4
5 - - - - - - - - - - - - - - - - 5
6 - - - - - - o - - - - - - - - - 6
7 - - - - - - - - - - - - - - - - 7
8 - - - - - - - - - - - - - - - - 8
9 - - - - - - - - - - - - - - - - 9
a - - - - - - - - - - - - - - - - a
b - - - - - - - - - - - - - - - - b
c - - - - - - - - - - - - - - - - c
d - - - - - - - - - - - - - - - - d
e - - - - - - - - - - - - - - - - e
f - - - - - - - - - - - - - - - - f
0 1 2 3 4 5 6 7 8 9 a b c d e f
best={"r":6,"c":7,"score":31}
0 1 2 3 4 5 6 7 8 9 a b c d e f
0 - - - - - - - - - - - - - - - - 0
1 - - - - - - - - - - - - - - - - 1
2 - - - - - - - - - - - - - - - - 2
3 - - - - - - - - - - - - - - - - 3
4 - - - - - - - - - - - - - - - - 4
5 - - - - - - - - - - - - - - - - 5
6 - - - - - - o x - - - - - - - - 6
7 - - - - - - - - - - - - - - - - 7
8 - - - - - - - - - - - - - - - - 8
9 - - - - - - - - - - - - - - - - 9
a - - - - - - - - - - - - - - - - a
b - - - - - - - - - - - - - - - - b
c - - - - - - - - - - - - - - - - c
d - - - - - - - - - - - - - - - - d
e - - - - - - - - - - - - - - - - e
f - - - - - - - - - - - - - - - - f
0 1 2 3 4 5 6 7 8 9 a b c d e f
...
best={"r":6,"c":3,"score":144}
0 1 2 3 4 5 6 7 8 9 a b c d e f
0 - - - - - - - - - - - - - - - - 0
1 - - - - - - - - - - - - - - - - 1
2 - - - - - - - - - - - - - - - - 2
3 - - - - - - - - - - - - - - - - 3
4 - - - - x - - - - - - - - - - - 4
5 - - - - - o - - - - - - - - - - 5
6 - - - x o o o x - - - - - - - - 6
7 - - - - - - - o - - - - - - - - 7
8 - - - - - - - - x - - - - - - - 8
9 - - - - - - - - - x - - - - - - 9
a - - - - - - - - - - - - - - - - a
b - - - - - - - - - - - - - - - - b
c - - - - - - - - - - - - - - - - c
d - - - - - - - - - - - - - - - - d
e - - - - - - - - - - - - - - - - e
f - - - - - - - - - - - - - - - - f
0 1 2 3 4 5 6 7 8 9 a b c d e f
...
0 1 2 3 4 5 6 7 8 9 a b c d e f
0 - - - - - - - - - - - - - - - - 0
1 - - - - - - - - - - - - - - - - 1
2 - - - - - - - - - - - - - - - - 2
3 - - - - - - - - - - - - - - - - 3
4 - - - - x - - - - - - - - - - - 4
5 - - o - - o - - - - - - - - - - 5
6 - - o x o o o x - - - - - - - - 6
7 - - - - x o o o - - - - - - - - 7
8 - - - - - x - - x - - - - - - - 8
9 - - - - - - x - - x - - - - - - 9
a - - - - - - - x - - - - - - - - a
b - - - - - - - - - - - - - - - - b
c - - - - - - - - - - - - - - - - c
d - - - - - - - - - - - - - - - - d
e - - - - - - - - - - - - - - - - e
f - - - - - - - - - - - - - - - - f
0 1 2 3 4 5 6 7 8 9 a b c d e f
x 贏了！參考文獻
電腦下棋的關鍵： Min-Max 對局搜尋與 Alpha-Beta 修剪算法
前言
雖然我們在前文設計五子棋程式時單純使用了盤面評估函數就已經設計出了「具備自動下棋能力的電腦程式」，但是這種設計方法是不夠強大的。
電腦下棋要夠強大，通常必須採用「Min-Max 對局搜尋法」，如果能夠搜尋得愈深，電腦的棋力通常就會越高。
但是、對於電腦而言，每一層都有很多可能的下法，對手也可能會有很多的回應方式，這樣一層一層下去會有組合爆炸的問題。
舉例而言，假如對上文中有 256 格的棋盤而言，第一子的下法有 256 種，第二子的下法就有 255 種，....
因此若我們要進行 n 層的徹底搜尋，那在下第一步之前就必須探詢 256255...*(256-n+1) 這麼多種可能性，當 n 超過 10 層時，幾乎任何電腦都不可能在短短數秒內完成這樣的搜尋。
於是我們就必須減少蒐尋的可能性，這時我們可以採用著名的「 Alpha-Beta Cut」修剪法來減少蒐尋的空間大小。
讓我們先來瞭解一下何謂 「Min-Max 對局搜尋法」。
Min-Max 對局搜尋法
在下棋的時候，如果要打敗對手，必須考量讓自己得分最多，且讓對手得分最少，Min-Max 正是根據這樣的想法而設計出來的。
必須注意的是，當電腦要下一子之前，當然會下讓自己得分最多的那一格，但是這很容易會落入對手的陷阱，因為得分最多的那一格很可能接下來失分更多。
於是、一個合理的想法是將所有層次分為「敵我雙方」兩類，我方下的那層得分越多越好，而對方下的那層失分越少越好。
而且、我們不能假設對方是個笨蛋，因此在每一層上，我們都必須認為「對方可能會下出讓我們失分最多的一步」，而我們必須盡可能選擇「最大失分最小化」的策略，這種想法就導出了「Min-Max 對局搜尋法」，以下是一個範例。
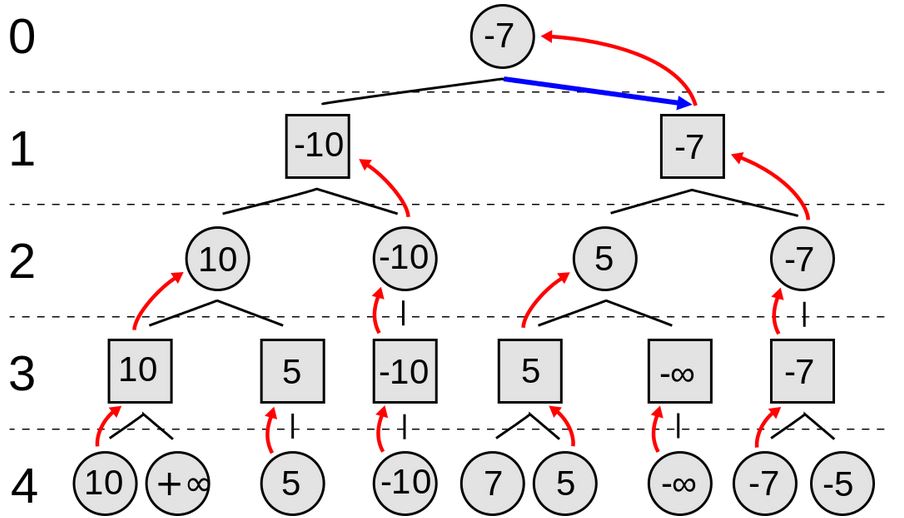
圖、Min-Max 對局搜尋法的範例
在上圖中、由於第 0 層代表我方下，所以我們取在第一層失分少的步驟，而第 1 層代表敵方下，所以假設他們也會採取對他們最有利的下法 (也就是對我們最不利的、讓我們失分多的) ，整張圖的推論邏輯就在這種 Min-Max 的過程中完成了。
必須補充說明的是，圖中的 -∞ 與 +∞ 通常代表該節點為樹葉節點，也就是整盤棋已經結束。換句話說、有人輸了或贏了。
演算法： Min-Max 對局搜尋
function minimax(node, depth, maximizingPlayer)
if depth = 0 or node is a terminal node
return the heuristic value of node
if maximizingPlayer
bestValue := -∞
for each child of node
val := minimax(child, depth - 1, FALSE))
bestValue := max(bestValue, val);
return bestValue
else
bestValue := +∞
for each child of node
val := minimax(child, depth - 1, TRUE))
bestValue := min(bestValue, val);
return bestValue
(* Initial call for maximizing player *)
minimax(origin, depth, TRUE)Alpha-Beta 修剪法
您可以看到 Min-Max 對每個節點都進行遞迴展開，這種展開的數量是很龐大的，因此即使電腦非常快也展開不了幾層，所以我們必須透過「Alpha-Beta 修剪法」減少展開的數量，以下是一個範例。
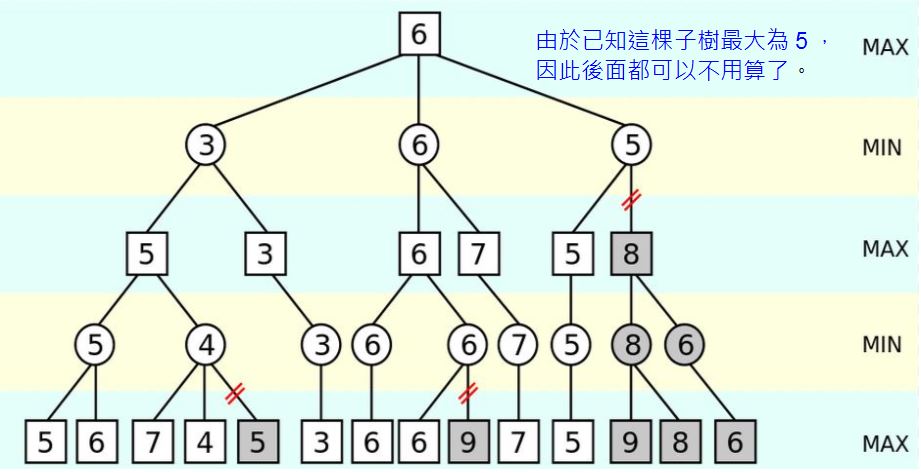
圖、 Alpha-Beta 修剪法的範例
在上圖中，請注意上面 Min 層的 5 節點，您可以看到當該節點最左邊子樹的分數 5 已經計算出來後，由於 5 比 8 還小，因此不管後面的節點分數為多少，都不可能讓其父節點變得比 5 還要大，所以右邊的子樹都可以不用再計算了，這就是 Alpha-Beta 修剪法的原理。
「Alpha-Beta 修剪法」其實是「Min-Max 對局搜尋法」的一個修改版，主要是在 Min-Max 當中加入了 α 與 β 兩個紀錄值，用來做為是否要修剪的參考標準，演算法如下所示。
function alphabeta(node, depth, α, β, maximizingPlayer)
if depth = 0 or node is a terminal node
return the heuristic value of node
if maximizingPlayer
for each child of node
α := max(α, alphabeta(child, depth - 1, α, β, FALSE))
if β ≤ α
break (* β cut-off *)
return α
else
for each child of node
β := min(β, alphabeta(child, depth - 1, α, β, TRUE))
if β ≤ α
break (* α cut-off *)
return β
(* Initial call for maximizing player *)
alphabeta(origin, depth, -∞, +∞, TRUE)結語
當然、 Alpha-Beta 修剪法並不保證能將對局樹修剪得非常小，而且樹的大小會與拜訪的順序有關，如果希望樹可以比較小的話，應當從「對我方分數最高、對敵方分數最低」的節點開始處理，這樣才能有效的降低整棵對局搜尋樹的大小。
參考文獻
【本文由陳鍾誠取材並修改自 維基百科，採用創作共用的 姓名標示、相同方式分享 授權】
程式與科學
Eugene Goostman 程式真的通過了圖靈測試嗎？ (作者：陳鍾誠)
前言
2014 年 6 月 9 日，我看到 inside 網站中有人發布了一個訊息 「電腦首度通過圖靈測試(36kr.com)」。 我的直覺反應是，這件事情勢必有假，於是一路追了下去。
Inside 的訊息其實是轉貼自 36氪這個來自中國的網站， 36氪網站的文章標是 「计算机首次通过图灵测试」 。
不仔細看文章的人，很可能會被誤導，認為電腦已經可以成功得欺騙人類，讓人以為他是一個真人，而且比率達到和真人一樣的水準，也就是「人類已經無法正確區分文字交談的對象到底是電腦還是人類了」。
但是、這樣的想法是錯的，文章中所說的 Eugene Goostman 這個軟體其實並沒有達到「完全能欺騙人類」的水準，因為他們所說的圖靈測試，和我所認知的圖靈測試，根本就是不同的東西。
圖靈測試是甚麼？
36氪文章中所說的 「图灵测试」 ，其實有連結到百度百科。百度百科裏對圖靈測試的描述如下：
图灵测试是测试人在与被测试者(一个人和一台机器)隔开的情况下，通过一些装置（如键盘）向被测试者随意提问。问过一些问题后，如果被测试者超过30%的答复不能使测试人确认出哪个是人、哪个是机器的回答，那么这台机器就通过了测试，并被认为具有人类智能。
但是、我所認知的圖靈測試，並不是採用 30% 誤判率為基準的，而是應該達到「和人類被誤判為電腦」一樣的水準。換句話說，假如程式偽裝的和真人一樣好的話，那麼應該要符合下列的表格要求。
| 判斷者的決定 | 交談對象為人類 | 交談對象為電腦程式 |
|---|---|---|
| 判斷為人 | 比率為 P (正確判斷) | 比率大於或等於為 P (欺騙成功) |
| 判斷為電腦 | 比率為 1-P (誤判人為電腦) | 比率小於或等於為 1-P (欺騙失敗) |
因此、對於上述新聞中所說的，「计算机首次通过图灵测试」 這件事情，其實是採用 30% 的欺騙成功率，這是我們認為該宣稱有問題的關鍵原因。
但是、為甚麼測試單位「英國雷丁大學」要採用 30% 做為圖靈測試是否通過的標準呢？我想原因應該來自於「圖靈」本人在那篇名為 「COMPUTING MACHINERY AND INTELLIGENCE 」的文章中所提到的一個預估，原文如下：
I believe that in about fifty years' time it will be possible to programme computers, with a storage capacity of about 10^9, to make them play the imitation game so well that an average interrogator will not have more than 70 percent chance of making the right identification after five minutes of questioning. … I believe that at the end of the century the use of words and general educated opinion will have altered so much that one will be able to speak of machines thinking without expecting to be contradicted.
在上文當中「圖靈」預估 50 年後電腦就可以讓不超過 70% 的人做正確的決定。換句話說，就是成功的欺騙過 30% 的人。於是「英國雷丁大學」就把這個預估當成圖靈測試的基準了。
但是、這只是圖靈的一個預估，並不代表圖靈測試就應該定為成功的欺騙過 30% 的人啊！ (而且這也不是學術界對圖靈測試的一個共識)。
測試單位的英文公告
36氪的 「计算机首次通过图灵测试」 一文中指出了訊息來源為「英國雷丁大學的新聞稿」，連結如下：
該新聞稿提到 Eugene Goostman 這個程式通過圖靈測試的語句如下：
The 65 year-old iconic Turing Test was passed for the very first time by supercomputer Eugene Goostman during Turing Test 2014 held at the renowned Royal Society in London on Saturday.
但新聞稿的後面有寫出測試方法的描述：
- Simultaneous tests as specified by Alan Turing
- Each judge was involved in five parallel tests - so 10 conversations
- 30 judges took part
- In total 300 conversations
- In each five minutes a judge was communicating with both a human and a machine
- Each of the five machines took part in 30 tests
- To ensure accuracy of results, Test was independently adjudicated by Professor John Barnden, University of Birmingham, formerly head of British AI Society
我對這個測試方法的解讀如下：
- 圖靈測試：電腦程式是否能成功的透過文字交談欺騙人類，偽裝自己是個人。
- 每個「判斷者」都會分別判斷五組「人+電腦」的配對，也就是總共進行 10 次的對話。
- 總共有 30 位判斷者參與。
- 總共有 30*10=300 場的交談。
- 在五分鐘內，「判斷者」會與一組「人和機器」分別交談。
- 五組「電腦程式」都會與 30 位「判斷者」談過一次。
- 為了確認「判斷者」判斷結果為正確或錯誤， John Barnden 教授會監控並確認結果。
問題在哪裡？
我認為「英國雷丁大學發布的新聞稿」用詞有欠妥當，主要是因為下列語句實在是太過強烈：
The 65 year-old iconic Turing Test was passed for the very first time by supercomputer Eugene Goostman during Turing Test 2014 held at the renowned Royal Society in London on Saturday.
雖然新聞稿後面有交代 Eugene Goostman 程式成功的欺騙過 33% 的判斷者，但是沒有看完全文的人還是很容易被誤導的。
If a computer is mistaken for a human more than 30% of the time during a series of five minute keyboard conversations it passes the test. No computer has ever achieved this, until now. Eugene managed to convince 33% of the human judges (30 judges took part - see more details below) that it was human.
而 36氪網站直接把 「计算机首次通过图灵测试」 拿來當標題，則是進一步的誤導了大家， 雖然 36氪有超連結指向 百度的圖靈測試定義 ，但是這個定義顯然與一般人的認知不同，應該要強調一下才對，不應該企圖用聳動性的標題吸引目光。
最後、 inside 的轉載 「電腦首度通過圖靈測試(36kr.com)」 這篇，雖然有指出來源的 36氪網站文章，不過我想轉貼的人或許沒有仔細想過到底文章中的「通過圖靈測試」到底是甚麼意義，也沒想過這樣可能會誤導讀者，造成錯誤科學訊息的傳播問題。
以前的程式表現如何？
事實上、能夠成功欺騙人類，讓某些人認為對方是真人的交談程式，在人工智慧的歷史上很早就出現過了。
遠在 1966 年時，Joseph Weizenbaum 就曾經創造出一個稱為 ELIZA 的程式，該程式採用了非常簡單的字串比對方法，結果竟然讓不少交談者認為 ELIZA 是個真人，以下是維基百科對 Eliza 程式的描述網址。
在 2013 年 8 月號的程式人雜誌當中，筆者也在文章中展示了一個自己寫的「中文版 Eliza 聊天程式」，有興趣的朋友也可以閱讀該文章順便瞭解這種程式是怎麼做的。
另外、在 2011 年時有一個稱為 Cleverbot 的程式 曾經創造過成功欺騙 60% 判斷者的紀錄，這個紀錄比這次比賽第一名的 Eugene Goostman 程式還要高。因此我們真的很難用「電腦首度通過圖靈測試」這樣的語句來描述這次比賽的結果，甚至這次比賽到底是否有創了什麼記錄都是很難確定的。
所以、我真的覺得這樣的訊息是過於聳動了，因此特別寫了這篇文章來提醒大家，避免很多人會被這些訊息誤導。
我的感想
從這個案例中，我們可以看到在網路訊息發達的今天，要能夠不被誤導，恐怕必須要有很強的判斷力與追根究柢的精神，但是在這個訊息多如牛毛的世界中，錯誤與聳動的訊息往往傳播的特別快，這恐怕是網路世界亟待解決的問題之一啊！
最後、我上 g0v 的新聞小幫手 去檢舉了這個新聞，希望能讓誤導的情況稍微降低一下，檢舉網址如下：
參考文獻
- http://en.wikipedia.org/wiki/ELIZA
- JavaScript (8) – 中文版 Eliza 聊天程式
- http://en.wikipedia.org/wiki/Cleverbot
- 36氪網站:「计算机首次通过图灵测试」 -- http://www.36kr.com/p/212680.html
- 百度百科：「图灵测试」 -- http://baike.baidu.com/view/94296.htm
- Inside 網站：「電腦首度通過圖靈測試(36kr.com)」 -- http://share.inside.com.tw/posts/5079
- TURING TEST SUCCESS MARKS MILESTONE IN COMPUTING HISTORY
- http://en.wikipedia.org/wiki/Turing_test
- http://www.wired.com/2014/06/turing-test-not-so-fast/
- http://plato.stanford.edu/entries/turing-test/
- 資訊科學到底算不算是科學呢？ -- http://pansci.tw/archives/44422
- COMPUTING MACHINERY AND INTELLIGENCE , By A. M. Turing -- http://www.csee.umbc.edu/courses/471/papers/turing.pdf
- 图灵测试，测的到底是什么？ -- http://www.guokr.com/article/438573/
程式人文集
從 Arduino 到 AVR 晶片(2) -- Interrupts 中斷處理 (作者：Cooper Maa)
什麼是 Interrupts?
當你在工作的時候，突然電話鈴聲響起，於是你把手邊工作停下來、接電話、講電話，然後回來繼續剛剛工作 －－ 這就是所謂的中斷 (Interrupt)，而電話便是中斷源。
在微控制器中，中斷的來源有很多，諸如 Reset, 外部中斷, Timer, USART, EEPROM, ADC 等。比如，當 Timer Overflow 時可以引發中斷，當 USART 收到資料或資料傳輸完畢時可以引發中斷…
跟人一樣，在遇到中斷的時候，微控制器的 CPU 也會把手邊的工作停下來，然後跳到預設的位址 (接電話)，接著執行一段程式 (講電話)，執行完後回來繼續進行剛剛的工作。
在發生中斷的時候，CPU 會老老實實的做這幾個動作：
- 執行當前的指令
- 把下一個指令的位址 push 到 stack 上，停止程式的正常流程，然後
- 跳到預設的位址，這個位址稱為中斷向量表，是由 MCU 製造商預先定義好的。 在中斷向量表中，每個中斷都有一個 entry，就看發生什麼中斷，CPU 就跳到哪個 entry。通常每個 entry 裏只是一條 JMP xxxx 的指令，會讓 CPU 輾轉跳到一段稱為中斷服務函式 (Interrupt Service Routine, ISR) 的副程式。
- 接著執行中斷服務函式
- 當執行完中斷服務函式後，再從 stack 上 pop 出指令的位址，並從它離開的地方繼續執行程式
電腦比人強的地方，在於它的記憶力好，沒健忘症，當 CPU 處理完中斷後，一定會回去進行原來的工作，除非程式開發者疏忽了把 ISR 寫成跳不出來的無窮迴圈。
Interrupt vectors
底下這張是 ATmega328 的中斷向量表：
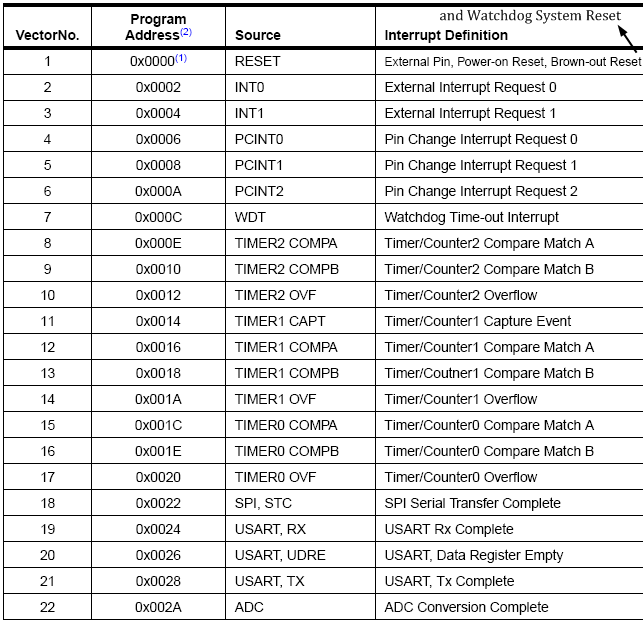
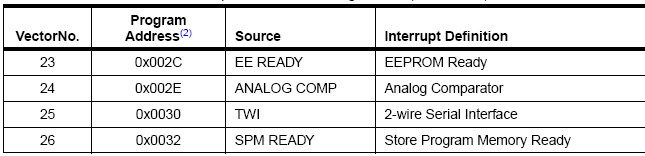
當中斷觸發時，CPU 會跳到預設的位址，例如當 ADC 轉換完成時會引發 ADC 中斷，CPU 這時就會跳到 0x002A 這個位址 (vector 22 所在的位址) 去執行指令。如前面說的，通常中斷向量表的每個 entry 裏只是一條 JMP xxxx 的指令，會讓 CPU 輾轉跳到中斷服務函式 (ISR)。
底下是中斷向量表典型的設定:
Address Labels Code Comments
0x0000 jmp RESET ; Reset Handler
0x0002 jmp EXT_INT0 ; IRQ0 Handler
0x0004 jmp EXT_INT1 ; IRQ1 Handler
0x0006 jmp PCINT0 ; PCINT0 Handler
0x0008 jmp PCINT1 ; PCINT1 Handler
0x000A jmp PCINT2 ; PCINT2 Handler
0x000C jmp WDT ; Watchdog Timer Handler
0x000E jmp TIM2_COMPA ; Timer2 Compare A Handler
0x0010 jmp TIM2_COMPB ; Timer2 Compare B Handler
0x0012 jmp TIM2_OVF ; Timer2 Overflow Handler
0x0014 jmp TIM1_CAPT ; Timer1 Capture Handler
0x0016 jmp TIM1_COMPA ; Timer1 Compare A Handler
0x0018 jmp TIM1_COMPB ; Timer1 Compare B Handler
0x001A jmp TIM1_OVF ; Timer1 Overflow Handler
0x001C jmp TIM0_COMPA ; Timer0 Compare A Handler
0x001E jmp TIM0_COMPB ; Timer0 Compare B Handler
0x0020 jmp TIM0_OVF ; Timer0 Overflow Handler
0x0022 jmp SPI_STC ; SPI Transfer Complete Handler
0x0024 jmp USART_RXC ; USART, RX Complete Handler
0x0026 jmp USART_UDRE ; USART, UDR Empty Handler
0x0028 jmp USART_TXC ; USART, TX Complete Handler
0x002A jmp ADC ; ADC Conversion Complete Handler
0x002C jmp EE_RDY ; EEPROM Ready Handler
0x002E jmp ANA_COMP ; Analog Comparator Handler
0x0030 jmp TWI ; 2-wire Serial Interface Handler
0x0032 jmp SPM_RDY ; Store Program Memory Ready Handler
;
0x0033RESET: ldi r16, high(RAMEND); Main program start
0x0034 out SPH,r16 ; Set Stack Pointer to top of RAM
0x0035 ldi r16, low(RAMEND)
0x0036 out SPL,r16
0x0037 sei ; Enable interrupts
0x0038 <instr> xxx以上面的程式為例，當發生 reset 中斷時，MCU 執行的第一條指令是 jmp RESET，因此會跳到 0x0033 的位址，亦即主程式的起始位置。假如是 ADC 中斷，MCU 會先跳到中斷向量表 0x002A 的位址，之後輾轉跳到 ADC 這個中斷服務函式。
Interrupt Service Routine (ISR)
在 Arduino 的程式中，要寫 ISR 是很簡單的一件事。你不需要自己設定中斷向量表，只要會使用 ISR() 這個巨集指令就可以了，例如:
ISR(ADC_vect)
{
// Your code here
}這表示這個是處理 ADC 轉換的中斷服務函式，將來當 ADC 轉換完成時會引發中斷，CPU 就會來執行這個中斷服務函式。
底下這張表列出了 ATmega328 的所有中斷向量，可在
| Vector | 說明 |
|---|---|
| INT0_vect | External Interrupt Request 0 |
| INT1_vect | External Interrupt Request 1 |
| PCINT0_vect | Pin Change Interrupt Request 0 |
| PCINT1_vect | Pin Change Interrupt Request 1 |
| PCINT2_vect | Pin Change Interrupt Request 2 |
| WDT_vect | Watchdog Time-out Interrupt |
| TIMER2_COMPA_vect | Timer/Counter2 Compare Match A |
| TIMER2_COMPB_vect | Timer/Counter2 Compare Match B |
| TIMER2_OVF_vect | Timer/Counter2 Overflow |
| TIMER1_CAPT_vect | Timer/Counter1 Capture Event |
| TIMER1_COMPA_vect | Timer/Counter1 Compare Match A |
| TIMER1_COMPB_vect | Timer/Counter1 Compare Match B |
| TIMER1_OVF_vect | Timer/Counter1 Overflow |
| TIMER0_COMPA_vect | TimerCounter0 Compare Match A |
| TIMER0_COMPB_vect | TimerCounter0 Compare Match B |
| TIMER0_OVF_vect | Timer/Couner0 Overflow |
| SPI_STC_vect | SPI Serial Transfer Complete |
| USART_RX_vect | USART Rx Complete |
| USART_UDRE_vect | USART, Data Register Empty |
| USART_TX_vect | USART Tx Complete |
| ADC_vect | ADC Conversion Complete |
| EE_READY_vect | EEPROM Ready |
| ANALOG_COMP_vect | Analog Comparator |
| TWI_vect | Two-wire Serial Interface |
| SPM_READY_vect | Store Program Memory Read |
外部中斷實驗 (External Interrupts)
實驗目的
練習處理外部中斷。在這個實驗中，你將利用 ISR() 巨集指令設定中斷服務函式 (Interrupt Service Routine, ISR)，讓程式在 pin 2 產生外部中斷時自動執行 ISR。
材料
- Arduino 主板 x 1
- LED x 1
- Pushbutton x 1
- 10K 歐姆電阻 x 1
- 麵包板 x 1
- 單心線 x N
接線
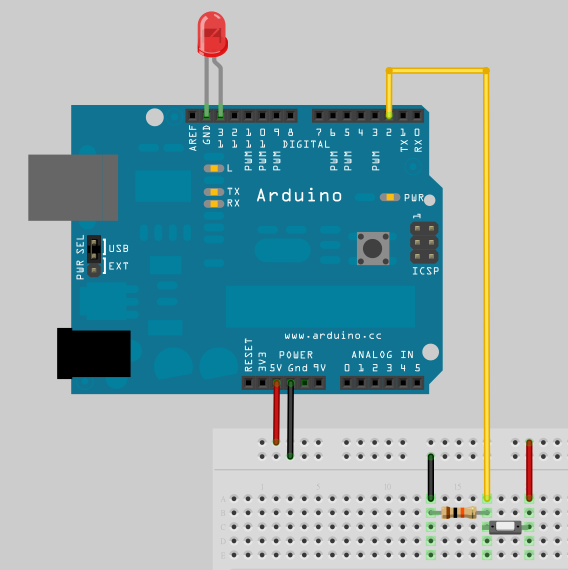
把 LED 接到 pin13，長腳 (陽極) 接到 pin13，短腳 (陰極) 接到 GND 把 pushbutton 一支腳接到 +5V，另一支腳接到 pin 2 同時接一顆 10K 電阻連到 GND
INT0 與 INT1 外部中斷
如下圖所示，ATmega328 有兩個外部中斷，編號 0 (INT0) 在 pin 2 上，而編號 1 (INT1) 在 pin 3 上:
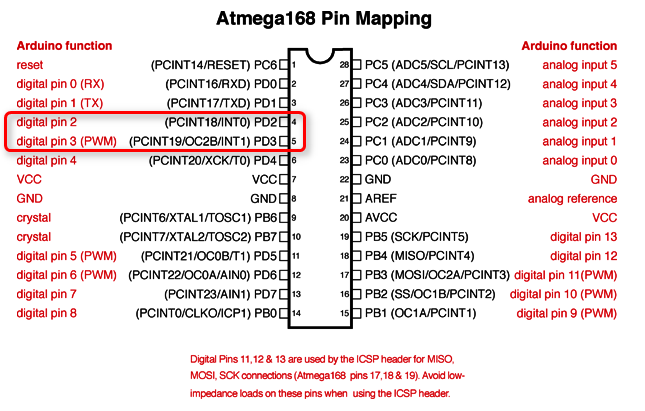
我們可以決定什麼時候要觸發 INT0 和 INT1 外部中斷，一共有四種狀況可以選擇:
- LOW: 當 pin 為 LOW 時觸發中斷
- CHANGE: 當 pin 狀態改變時觸發中斷，不管是從 HIGH 到 LOW 或從 LOW 到 HIGH
- FALLING: 當 pin 狀態從 HIGH 到 LOW 時觸發中斷，又稱負緣觸發
- RISING: 當 pin 狀態從 LOW 到 HIGH 時觸發中斷，又稱正緣觸發
選擇的方法是透過 ECIRA (External Interrupt Control Register A) 這個暫存器:
▲ 資料來源: ATmega168/328 Datasheet
以 INT0 外部中斷為例，假如我們希望 pin 2 狀態一有改變就觸發中斷，那麼就要把 ISC01 和 ISC00 設成 01:
EICRA &= ~_BV(ISC01); // pin 狀態改變時觸發中斷
EICRA |= _BV(ISC00); 除此以外，我們還要設定 EIMSK (External Interrupt Mask Register) 暫存器以啟用 INT0 或 INT1 中斷:
以 INT0 外部中斷為例，要啟用 INT0 外部中斷，得把 INT0 這個位元設成 1:
EIMSK |= _BV(INT0); // enable INT0程式
先來看使用 attachInterrupt() 函式的版本(attachInterrupt.pde)，這我們在「 attachInterrupt() 與外部中斷 」一文中介紹過，程式的邏輯是，當按鍵被按下時打開 LED 燈號，在按鍵放開時關閉 LED 燈號:
/*
* attachInterrupt.pde: attachInterrupt() 與外部中斷
*/
const int interruptNumber = 0; // Interrupt 0 在 pin 2 上
const int buttonPin = 2; // 按鈕(pushbutton)
const int ledPin = 13; // LED
volatile int buttonState; // 用來儲存按鈕狀態
void setup() {
pinMode(ledPin, OUTPUT); // 把 ledPin 設置成 OUTPUT
pinMode(buttonPin, INPUT); // 把 buttonPin 設置成 INPUT
// 把外部中斷(interrupt 0)連接到 buttonStateChanged() 函式
// CHANGE 是指當 pin 狀態改變時就觸發中斷，不管是從 HIGH 到 LOW 或從 LOW 到 HIGH
attachInterrupt(interruptNumber, buttonStateChanged, CHANGE);
}
void loop() {
// do nothing
}
// Interrupt 0 的中斷處理函式
// 讀取 buttonPin 的狀態，並反應到 ledPin 上
void buttonStateChanged() {
buttonState = digitalRead(buttonPin);
digitalWrite(ledPin, buttonState);
}要特別注意是，程式裏的 buttonState 變數是宣告成 volatile，這樣做的目的是告訴 Compiler 不要做最佳化，避免變數狀態不同步。給你一個建議，程式主體跟 ISR 都會用到的變數，盡可能把它宣告成 volatile。
接下來是改成用 EICRA 和 EIMSK 暫存器和 ISR() 巨集指令的版本:
/*
* externalInterrupt.pde: INT 0 外部中斷
*/
const int interruptNumber = 0; // Interrupt 0 在 pin 2 上
const int buttonPin = 2; // 按鈕(pushbutton)
const int ledPin = 13; // LED
volatile int buttonState; // 用來儲存按鈕狀態
void setup() {
pinMode(ledPin, OUTPUT); // 把 ledPin 設置成 OUTPUT
pinMode(buttonPin, INPUT); // 把 buttonPin 設置成 INPUT
EIMSK |= _BV(INT0); // enable INT 0
EICRA &= ~_BV(ISC01); // pin 狀態改變時觸發中斷
EICRA |= _BV(ISC00);
}
void loop() {
// do nothing
}
// 讀取 buttonPin 的狀態，並反應到 ledPin 上
void buttonStateChanged() {
buttonState = digitalRead(buttonPin);
digitalWrite(ledPin, buttonState);
}
// Interrupt 0 的中斷處理函式
ISR(INT0_vect) {
buttonStateChanged();
}簡單的說，要處理 INT0 外部中斷，有三個步驟要做:
- 用 ISR() 巨集指令定義中斷服務函式
- 設定 EIMSK 暫存器啟用 INT0 中斷
- 設定 EICRA 暫存器決定什麼時候該觸發中斷
_BV() 巨集我們在「2.2) Blink part2」一文中已經介紹過，如果不想使用 _BV()，這樣寫也是可以的:
EIMSK |= (1 << INT0); // enable INT 0
EICRA |= (1 << ISC00); // pin 狀態改變時觸發中斷
EICRA &= ~(1 << ISC01);另外，ISR() 巨集指令也可以改用 SIGNAL() 巨集指令，SIGNAL() 是早期寫 ISR 的巨集指令。建議你盡可能使用 ISR() 巨集指令，因為 ISR() 比較直覺，只不過你必須知道 SIGNAL() 和 ISR() 幾乎是一樣的東西，而且很多前輩留下的 AVR 程式是用 SIGNAL() 巨集指令。
延伸閱讀
【本文作者為馬萬圳，原文網址為： http://coopermaa2nd.blogspot.tw/2011/04/3-interrupts.html , http://coopermaa2nd.blogspot.tw/2011/07/31-external-interrupts.html ，由陳鍾誠編輯後納入本雜誌】
對數 (logarithm) (作者：Bridan)
以前曾經寫文說明 開根號 的數學計算，今天就說明工程計算機另一重要計算功能 ─ 對數 。
對數的發明，是因為數學家想簡化算數乘除計算的繁瑣，對數的方法於1614年被約翰·納皮爾 (John Napier) 在 Mirifici Logarithmorum Canonis Descriptio (Description of the Wonderful Rule of Logarithms) 書中首次公開，而對數符號 log 來自拉丁文 logarithm，是由義大利數學家卡瓦列里 (Cavalieri，1598 - 1647) 所提出。
對數的觀念簡單的說，把數值乘除轉換成數值加減，在計算機發明前需要查表換算，加減計算後再反查表求出最後答案，因此有人發明 計算尺 ，解決查表換算問題。
log(X*Y) = log(X) + log(Y)
log(X/Y) = log(X) - log(Y)
log(Xa) = a * log(X)另外，為了區別以 10 為基底及 超越數 e (Euler's number) 為基底的對數，數學習慣分別表示為 log(X)和 ln(X)，而計算機語言喜歡用 log10(X)及 log(X)表示。在日常應用方面，由於人類對外界感覺的魯鈍，也運用了許多對數的觀念，例如，聲音用分貝、地震用芮氏規模、天文觀測用星等，意思是訊號要變化很大，人們才會有所感覺。
回歸主題，本文的要點為計算機如何計算對數值？在 資料型態認識─浮點數 (single ＆ double) 一文提到，任何正實數可以表示為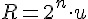 
， 是整數， 
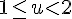，那
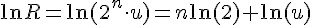
接下來就要思考如何計算 ln(u)，這需要 從等比級數和說起，令 Y 為等比級數和，將它減掉與 x 相乘的值等於 1，因此 Y 可得一個生成函數 1/(1-x)。
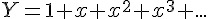
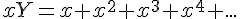
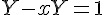
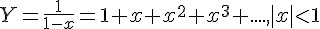
如果要讓等比級數和 Y 收斂等於生成函數，其要件為 |x|＜1。然後將 Y 對 x 積分可得，
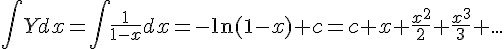
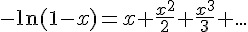
將上式 x 改以 -x 代入
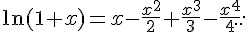
然後兩式合併
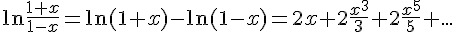
可能有人看到這裡，覺得越搞越複雜，其實這是計算機快速收斂最好的方法，因為計算 ln(1+x)將需要計算更多項次才能達到更好的精確度， 如果要精確到小數第 n 位，必須算到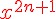 
。那如何求出 x，令
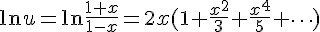
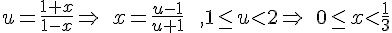
以上是超越數 e 為基底的對數計算，若想計算以 10 為基底的對數可以利用下列公式換算
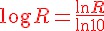
(本文來自「研發養成所」 Bridan 的網誌，原文網址為 http://4rdp.blogspot.tw/2014/06/logarithm.html ，由陳鍾誠編輯後納入程式人雜誌)
[PhoneGap] Google Map (作者：廖憲得 0xde)
<!DOCTYPE html>
<html>
<head>
<meta http-equiv="content-type" content="text/html; charset=UTF-8" />
<script
src="http://maps.googleapis.com/maps/api/js?key=AIzaSyDY0kkJiTPVd2U7aTOAwhc9ySH6oHxOIYM&sensor=false">
</script>
<script>
var map;
function initialize()
{
var mapOpt = {
center:new google.maps.LatLng(24.150026,120.683868),
zoom:15,
mapTypeId:google.maps.MapTypeId.ROADMAP,
mapTypeControl: false,
navigationControl : false,
scaleControl : false,
streetViewControl: false
};
map=new google.maps.Map(document.getElementById("googleMap"),mapOpt);
}
function Reinitialize(MapX,MapY)
{
var mapOpt = {
center:new google.maps.LatLng(MapX,MapY),
zoom:15,
mapTypeId:google.maps.MapTypeId.ROADMAP,
mapTypeControl: false,
navigationControl : false,
scaleControl : false,
streetViewControl: false
};
map=new google.maps.Map(document.getElementById("googleMap"),mapOpt);
}
google.maps.event.addDomListener(window, 'load',initialize);
</script>
</head>
<body>
<button onclick="map.setMapTypeId(google.maps.MapTypeId.ROADMAP);">道路地圖</button>
<button onclick="map.setMapTypeId(google.maps.MapTypeId.SATELLITE);">衛星地圖</button>
<button onclick="map.setMapTypeId(google.maps.MapTypeId.HYBRID);">混合地圖</button>
<button onclick="map.setMapTypeId(google.maps.MapTypeId.TERRAIN);">實際地圖</button>
請輸入經緯度：
<input id="XX" type="text" style="width:80px" >
<input ID="YY" type="text" style="width:80px" >
<button onclick="Reinitialize(XX.value,YY.value)">搜尋經緯度</button>
<div id="googleMap" style="width:400px;height:300px;"></div>
</body>
</html>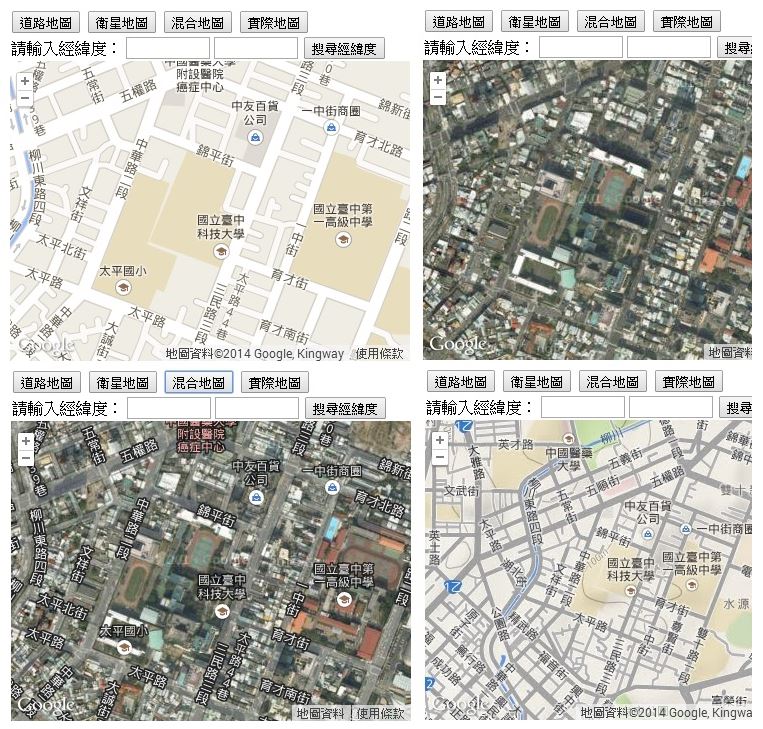
【本文作者為「廖憲得」，原文網址為： http://www.dotblogs.com.tw/0xde/archive/2014/06/27/145727.aspx ，由陳鍾誠編輯後納入本雜誌】
開放電腦計畫 (12) – 使用區塊式方法設計 MCU0 的 Verilog 程式 (作者：陳鍾誠)
前言
我們曾經在下列文章中設計出了 MCU0 迷你版這個只有六個指令的微控制器，整個實作只有 51 行。
但是、上述程式雖然簡單，但卻是採用流程式的寫法。雖然、筆者不覺得流程式的寫法有甚麼特別的缺陷，但是對那些習慣採用硬體角度設計 Verilog 程式的人而言，似乎採用「區塊式的設計方式」才是正統，所以、筆者將於本文中採用「區塊式的方式重新設計」MCU0 迷你版，以便能學習「硬體設計者」的思考方式。
MCU0 迷你版的指令表
為了方便讀者閱讀，不需要查閱前文，我們再次列出了 MCU0 迷你版的指令表如下：
| OP | name | 格式 意 | 義 |
|---|---|---|---|
| 0 | LD | LD C | A = [C] |
| 1 | ADD | ADD C | A = A + [C] |
| 2 | JMP | JMP C | PC = C |
| 3 | ST | ST C | [C] = A |
| 4 | CMP | CMP C | SW = A CMP [C] |
| 5 | JEQ | JEQ C | if SW[30]=Z=1 then PC = C |
MCU0 迷你版的區塊設計圖
在MCU0 迷你版裏，總共有三個暫存器，分別是 A, PC 與 SW，一個具有兩組讀取 (i1/d1, i2/d2) 與一組寫入的記憶體 (wi/wd)，還有一個算術邏輯單元 ALU，這個電路的設計圖如下。
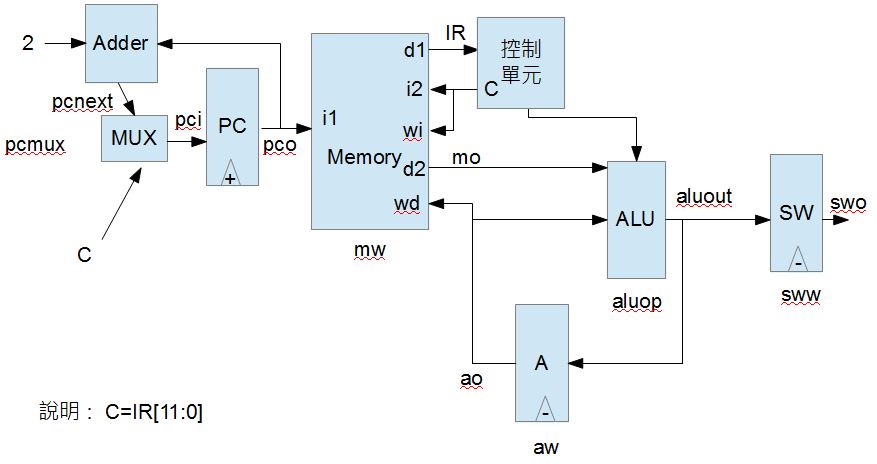
圖、MCU0bm 的區塊設計圖
由於筆者不熟悉數位電路設計的繪圖軟體，因此就簡單的用 LibreOffice 的 Impress 繪製了上圖，純粹採用區塊表達法，並沒有使用標準的數位電路設計圖示。
原始碼
根據上圖，我們設計出了下列 Verilog 程式，您應該可以很清楚的找出程式與圖形之間的對應關係。
module memory(input w, input [11:0] wi, input [15:0] wd, input [11:0] i1, output [15:0] d1, input [11:0] i2, output [15:0] d2);
integer i;
reg [7:0] m[0:2**12-1];
initial begin
$readmemh("mcu0m.hex", m);
for (i=0; i < 32; i=i+2) begin
$display("%x: %x", i, {m[i], m[i+1]});
end
end
assign d1 = {m[i1], m[i1+1]};
assign d2 = {m[i2], m[i2+1]};
always @(w) begin
if (w) {m[wi], m[wi+1]} = wd;
end
endmodule
module adder#(parameter W=16)(input [W-1:0] a, input [W-1:0] b, output [W-1:0] c);
assign c = a + b;
endmodule
module register#(parameter W=16)(input clock, w, input [W-1:0] ri, output [W-1:0] ro);
reg [W-1:0] r;
always @(posedge clock) begin
if (w) r = ri;
end
assign ro=r;
endmodule
module alu(input [3:0] op, input [15:0] a, input [15:0] b, output reg [15:0] c);
parameter [3:0] ZERO=4'h0, ADD=4'h1, CMP=4'he, APASS=4'hf;
always @(*) begin
case (op)
ADD: c = a+b;
CMP: begin c[15]=(a < b); c[14]=(a==b); c[13:0]=14'h0; end
APASS: c = a;
default: c = 0;
endcase
end
endmodule
module mux#(parameter W=16)(input sel, input [W-1:0] i0, i1, output [W-1:0] o);
assign o=(sel)?i1:i0;
endmodule
`define OP ir[15:12]
`define C ir[11:0]
`define N SW.r[15]
`define Z SW.r[14]
module mcu(input clock);
parameter [3:0] LD=4'h0,ADD=4'h1,JMP=4'h2,ST=4'h3,CMP=4'h4,JEQ=4'h5;
reg mw, aw, pcmux, sww;
reg [3:0] aluop;
wire [11:0] pco, pci, pcnext;
wire [15:0] aluout, ao, swo, ir, mo;
register#(.W(12)) PC(clock, 1, pci, pco);
adder#(.W(12)) adder0(2, pco, pcnext);
memory mem(mw, `C, ao, pco[11:0], ir, `C, mo);
register#(.W(16)) A(~clock, aw, aluout, ao);
register#(.W(16)) SW(~clock, sww, aluout, swo);
alu alu0(aluop, mo, ao, aluout);
mux#(.W(12)) muxpc(pcmux, pcnext, `C, pci);
initial begin
PC.r = 0; SW.r = 0; mw = 0; aw = 0; pcmux=0; sww=0; aluop=alu0.ZERO;
end
always @(ir or mo or A.r) begin
mw = 0;
aw = 0;
sww = 0;
pcmux = 0;
aluop = alu0.ZERO;
case (`OP)
LD: begin aw=1; aluop=alu0.APASS; end // LD C
ST: mw=1; // ST C
JMP: pcmux=1; // JMP C
JEQ: if (`Z) pcmux=1; // JEQ C
CMP: begin sww=1; aluop = alu0.CMP; end // CMP C
ADD: begin aw=1; aluop=alu0.ADD; end // ADD C
endcase
end
endmodule
module main; // 測試程式開始
reg clock; // 時脈 clock 變數
mcu mcu0(clock);
initial begin
clock = 0;
$monitor("%4dns pc=%x ir=%x mo=%x sw=%x a=%d mw=%b aluout=%x", $stime, mcu0.PC.r, mcu0.ir, mcu0.mo, mcu0.SW.r, mcu0.A.r, mcu0.mw, mcu0.aluout);
#1000 $finish;
end
always #5 begin
clock=~clock; // 每隔 5ns 反相，時脈週期為 10ns
end
endmodule輸入的機器碼 mcu0m.hex
為了測試上述程式，我們同樣採用了計算 SUM=1+2+...+10 的這個程式作為輸入，以下是機器碼與對應的組合語言程式。
00 16 // 00 LOOP: LD I
40 1A // 02 CMP N
50 12 // 04 JEQ EXIT
10 18 // 06 ADD K1
30 16 // 08 ST I
00 14 // 0A LD SUM
10 16 // 0C ADD I
30 14 // 0E ST SUM
20 00 // 10 JMP LOOP
20 12 // 12 EXIT: JMP EXIT
00 00 // 14 SUM: WORD 0
00 00 // 16 I: WORD 0
00 01 // 18 K1: WORD 1
00 0A // 1A N: WORD 10 執行結果
編寫完成之後，我們就可以測試整個 mcu0bm.v 程式了，其執行結果如下所示。
C:\Dropbox\Public\web\oc\code\mcu0>iverilog mcu0bm.v -o mcu0bm
C:\Dropbox\Public\web\oc\code\mcu0>vvp mcu0bm
WARNING: mcu0bm.v:5: $readmemh(mcu0m.hex): Not enough words in the file for the
requested range [0:4095].
00000000: 0016
00000002: 401a
00000004: 5012
00000006: 1018
00000008: 3016
0000000a: 0014
0000000c: 1016
0000000e: 3014
00000010: 2000
00000012: 2012
00000014: 0000
00000016: 0000
00000018: 0001
0000001a: 000a
0000001c: xxxx
0000001e: xxxx
0ns pc=000 ir=0016 mo=0000 sw=0000 a= 0 mw=0 aluout=0000
5ns pc=002 ir=401a mo=000a sw=0000 a= 0 mw=0 aluout=0000
15ns pc=004 ir=5012 mo=2012 sw=0000 a= 0 mw=0 aluout=0000
25ns pc=006 ir=1018 mo=0001 sw=0000 a= 0 mw=0 aluout=0001
30ns pc=006 ir=1018 mo=0001 sw=0000 a= 1 mw=0 aluout=0002
35ns pc=008 ir=3016 mo=0001 sw=0000 a= 1 mw=1 aluout=0000
45ns pc=00a ir=0014 mo=0000 sw=0000 a= 1 mw=0 aluout=0000
50ns pc=00a ir=0014 mo=0000 sw=0000 a= 0 mw=0 aluout=0000
55ns pc=00c ir=1016 mo=0001 sw=0000 a= 0 mw=0 aluout=0001
60ns pc=00c ir=1016 mo=0001 sw=0000 a= 1 mw=0 aluout=0002
65ns pc=00e ir=3014 mo=0001 sw=0000 a= 1 mw=1 aluout=0000
75ns pc=010 ir=2000 mo=0016 sw=0000 a= 1 mw=0 aluout=0000
85ns pc=000 ir=0016 mo=0001 sw=0000 a= 1 mw=0 aluout=0001
95ns pc=002 ir=401a mo=000a sw=0000 a= 1 mw=0 aluout=0000
105ns pc=004 ir=5012 mo=2012 sw=0000 a= 1 mw=0 aluout=0000
115ns pc=006 ir=1018 mo=0001 sw=0000 a= 1 mw=0 aluout=0002
120ns pc=006 ir=1018 mo=0001 sw=0000 a= 2 mw=0 aluout=0003
125ns pc=008 ir=3016 mo=0002 sw=0000 a= 2 mw=1 aluout=0000
135ns pc=00a ir=0014 mo=0001 sw=0000 a= 2 mw=0 aluout=0001
140ns pc=00a ir=0014 mo=0001 sw=0000 a= 1 mw=0 aluout=0001
145ns pc=00c ir=1016 mo=0002 sw=0000 a= 1 mw=0 aluout=0003
150ns pc=00c ir=1016 mo=0002 sw=0000 a= 3 mw=0 aluout=0005
155ns pc=00e ir=3014 mo=0003 sw=0000 a= 3 mw=1 aluout=0000
165ns pc=010 ir=2000 mo=0016 sw=0000 a= 3 mw=0 aluout=0000
175ns pc=000 ir=0016 mo=0002 sw=0000 a= 3 mw=0 aluout=0002
180ns pc=000 ir=0016 mo=0002 sw=0000 a= 2 mw=0 aluout=0002
185ns pc=002 ir=401a mo=000a sw=0000 a= 2 mw=0 aluout=0000
195ns pc=004 ir=5012 mo=2012 sw=0000 a= 2 mw=0 aluout=0000
205ns pc=006 ir=1018 mo=0001 sw=0000 a= 2 mw=0 aluout=0003
210ns pc=006 ir=1018 mo=0001 sw=0000 a= 3 mw=0 aluout=0004
215ns pc=008 ir=3016 mo=0003 sw=0000 a= 3 mw=1 aluout=0000
225ns pc=00a ir=0014 mo=0003 sw=0000 a= 3 mw=0 aluout=0003
235ns pc=00c ir=1016 mo=0003 sw=0000 a= 3 mw=0 aluout=0006
240ns pc=00c ir=1016 mo=0003 sw=0000 a= 6 mw=0 aluout=0009
245ns pc=00e ir=3014 mo=0006 sw=0000 a= 6 mw=1 aluout=0000
255ns pc=010 ir=2000 mo=0016 sw=0000 a= 6 mw=0 aluout=0000
265ns pc=000 ir=0016 mo=0003 sw=0000 a= 6 mw=0 aluout=0003
270ns pc=000 ir=0016 mo=0003 sw=0000 a= 3 mw=0 aluout=0003
275ns pc=002 ir=401a mo=000a sw=0000 a= 3 mw=0 aluout=0000
285ns pc=004 ir=5012 mo=2012 sw=0000 a= 3 mw=0 aluout=0000
295ns pc=006 ir=1018 mo=0001 sw=0000 a= 3 mw=0 aluout=0004
300ns pc=006 ir=1018 mo=0001 sw=0000 a= 4 mw=0 aluout=0005
305ns pc=008 ir=3016 mo=0004 sw=0000 a= 4 mw=1 aluout=0000
315ns pc=00a ir=0014 mo=0006 sw=0000 a= 4 mw=0 aluout=0006
320ns pc=00a ir=0014 mo=0006 sw=0000 a= 6 mw=0 aluout=0006
325ns pc=00c ir=1016 mo=0004 sw=0000 a= 6 mw=0 aluout=000a
330ns pc=00c ir=1016 mo=0004 sw=0000 a= 10 mw=0 aluout=000e
335ns pc=00e ir=3014 mo=000a sw=0000 a= 10 mw=1 aluout=0000
345ns pc=010 ir=2000 mo=0016 sw=0000 a= 10 mw=0 aluout=0000
355ns pc=000 ir=0016 mo=0004 sw=0000 a= 10 mw=0 aluout=0004
360ns pc=000 ir=0016 mo=0004 sw=0000 a= 4 mw=0 aluout=0004
365ns pc=002 ir=401a mo=000a sw=0000 a= 4 mw=0 aluout=0000
375ns pc=004 ir=5012 mo=2012 sw=0000 a= 4 mw=0 aluout=0000
385ns pc=006 ir=1018 mo=0001 sw=0000 a= 4 mw=0 aluout=0005
390ns pc=006 ir=1018 mo=0001 sw=0000 a= 5 mw=0 aluout=0006
395ns pc=008 ir=3016 mo=0005 sw=0000 a= 5 mw=1 aluout=0000
405ns pc=00a ir=0014 mo=000a sw=0000 a= 5 mw=0 aluout=000a
410ns pc=00a ir=0014 mo=000a sw=0000 a= 10 mw=0 aluout=000a
415ns pc=00c ir=1016 mo=0005 sw=0000 a= 10 mw=0 aluout=000f
420ns pc=00c ir=1016 mo=0005 sw=0000 a= 15 mw=0 aluout=0014
425ns pc=00e ir=3014 mo=000f sw=0000 a= 15 mw=1 aluout=0000
435ns pc=010 ir=2000 mo=0016 sw=0000 a= 15 mw=0 aluout=0000
445ns pc=000 ir=0016 mo=0005 sw=0000 a= 15 mw=0 aluout=0005
450ns pc=000 ir=0016 mo=0005 sw=0000 a= 5 mw=0 aluout=0005
455ns pc=002 ir=401a mo=000a sw=0000 a= 5 mw=0 aluout=0000
465ns pc=004 ir=5012 mo=2012 sw=0000 a= 5 mw=0 aluout=0000
475ns pc=006 ir=1018 mo=0001 sw=0000 a= 5 mw=0 aluout=0006
480ns pc=006 ir=1018 mo=0001 sw=0000 a= 6 mw=0 aluout=0007
485ns pc=008 ir=3016 mo=0006 sw=0000 a= 6 mw=1 aluout=0000
495ns pc=00a ir=0014 mo=000f sw=0000 a= 6 mw=0 aluout=000f
500ns pc=00a ir=0014 mo=000f sw=0000 a= 15 mw=0 aluout=000f
505ns pc=00c ir=1016 mo=0006 sw=0000 a= 15 mw=0 aluout=0015
510ns pc=00c ir=1016 mo=0006 sw=0000 a= 21 mw=0 aluout=001b
515ns pc=00e ir=3014 mo=0015 sw=0000 a= 21 mw=1 aluout=0000
525ns pc=010 ir=2000 mo=0016 sw=0000 a= 21 mw=0 aluout=0000
535ns pc=000 ir=0016 mo=0006 sw=0000 a= 21 mw=0 aluout=0006
540ns pc=000 ir=0016 mo=0006 sw=0000 a= 6 mw=0 aluout=0006
545ns pc=002 ir=401a mo=000a sw=0000 a= 6 mw=0 aluout=0000
555ns pc=004 ir=5012 mo=2012 sw=0000 a= 6 mw=0 aluout=0000
565ns pc=006 ir=1018 mo=0001 sw=0000 a= 6 mw=0 aluout=0007
570ns pc=006 ir=1018 mo=0001 sw=0000 a= 7 mw=0 aluout=0008
575ns pc=008 ir=3016 mo=0007 sw=0000 a= 7 mw=1 aluout=0000
585ns pc=00a ir=0014 mo=0015 sw=0000 a= 7 mw=0 aluout=0015
590ns pc=00a ir=0014 mo=0015 sw=0000 a= 21 mw=0 aluout=0015
595ns pc=00c ir=1016 mo=0007 sw=0000 a= 21 mw=0 aluout=001c
600ns pc=00c ir=1016 mo=0007 sw=0000 a= 28 mw=0 aluout=0023
605ns pc=00e ir=3014 mo=001c sw=0000 a= 28 mw=1 aluout=0000
615ns pc=010 ir=2000 mo=0016 sw=0000 a= 28 mw=0 aluout=0000
625ns pc=000 ir=0016 mo=0007 sw=0000 a= 28 mw=0 aluout=0007
630ns pc=000 ir=0016 mo=0007 sw=0000 a= 7 mw=0 aluout=0007
635ns pc=002 ir=401a mo=000a sw=0000 a= 7 mw=0 aluout=0000
645ns pc=004 ir=5012 mo=2012 sw=0000 a= 7 mw=0 aluout=0000
655ns pc=006 ir=1018 mo=0001 sw=0000 a= 7 mw=0 aluout=0008
660ns pc=006 ir=1018 mo=0001 sw=0000 a= 8 mw=0 aluout=0009
665ns pc=008 ir=3016 mo=0008 sw=0000 a= 8 mw=1 aluout=0000
675ns pc=00a ir=0014 mo=001c sw=0000 a= 8 mw=0 aluout=001c
680ns pc=00a ir=0014 mo=001c sw=0000 a= 28 mw=0 aluout=001c
685ns pc=00c ir=1016 mo=0008 sw=0000 a= 28 mw=0 aluout=0024
690ns pc=00c ir=1016 mo=0008 sw=0000 a= 36 mw=0 aluout=002c
695ns pc=00e ir=3014 mo=0024 sw=0000 a= 36 mw=1 aluout=0000
705ns pc=010 ir=2000 mo=0016 sw=0000 a= 36 mw=0 aluout=0000
715ns pc=000 ir=0016 mo=0008 sw=0000 a= 36 mw=0 aluout=0008
720ns pc=000 ir=0016 mo=0008 sw=0000 a= 8 mw=0 aluout=0008
725ns pc=002 ir=401a mo=000a sw=0000 a= 8 mw=0 aluout=0000
735ns pc=004 ir=5012 mo=2012 sw=0000 a= 8 mw=0 aluout=0000
745ns pc=006 ir=1018 mo=0001 sw=0000 a= 8 mw=0 aluout=0009
750ns pc=006 ir=1018 mo=0001 sw=0000 a= 9 mw=0 aluout=000a
755ns pc=008 ir=3016 mo=0009 sw=0000 a= 9 mw=1 aluout=0000
765ns pc=00a ir=0014 mo=0024 sw=0000 a= 9 mw=0 aluout=0024
770ns pc=00a ir=0014 mo=0024 sw=0000 a= 36 mw=0 aluout=0024
775ns pc=00c ir=1016 mo=0009 sw=0000 a= 36 mw=0 aluout=002d
780ns pc=00c ir=1016 mo=0009 sw=0000 a= 45 mw=0 aluout=0036
785ns pc=00e ir=3014 mo=002d sw=0000 a= 45 mw=1 aluout=0000
795ns pc=010 ir=2000 mo=0016 sw=0000 a= 45 mw=0 aluout=0000
805ns pc=000 ir=0016 mo=0009 sw=0000 a= 45 mw=0 aluout=0009
810ns pc=000 ir=0016 mo=0009 sw=0000 a= 9 mw=0 aluout=0009
815ns pc=002 ir=401a mo=000a sw=0000 a= 9 mw=0 aluout=0000
825ns pc=004 ir=5012 mo=2012 sw=0000 a= 9 mw=0 aluout=0000
835ns pc=006 ir=1018 mo=0001 sw=0000 a= 9 mw=0 aluout=000a
840ns pc=006 ir=1018 mo=0001 sw=0000 a= 10 mw=0 aluout=000b
845ns pc=008 ir=3016 mo=000a sw=0000 a= 10 mw=1 aluout=0000
855ns pc=00a ir=0014 mo=002d sw=0000 a= 10 mw=0 aluout=002d
860ns pc=00a ir=0014 mo=002d sw=0000 a= 45 mw=0 aluout=002d
865ns pc=00c ir=1016 mo=000a sw=0000 a= 45 mw=0 aluout=0037
870ns pc=00c ir=1016 mo=000a sw=0000 a= 55 mw=0 aluout=0041
875ns pc=00e ir=3014 mo=0037 sw=0000 a= 55 mw=1 aluout=0000
885ns pc=010 ir=2000 mo=0016 sw=0000 a= 55 mw=0 aluout=0000
895ns pc=000 ir=0016 mo=000a sw=0000 a= 55 mw=0 aluout=000a
900ns pc=000 ir=0016 mo=000a sw=0000 a= 10 mw=0 aluout=000a
905ns pc=002 ir=401a mo=000a sw=0000 a= 10 mw=0 aluout=4000
910ns pc=002 ir=401a mo=000a sw=4000 a= 10 mw=0 aluout=4000
915ns pc=004 ir=5012 mo=2012 sw=4000 a= 10 mw=0 aluout=0000
925ns pc=012 ir=2012 mo=2012 sw=4000 a= 10 mw=0 aluout=0000您可以清楚的看到，該程式在 870ns 時計算出了總合 SUM=55 的結果，這代表 mcu0bm.v 的設計完成了計算 1+...+10 的功能。
結語
在上述實作中，採用區塊式設計的 mcu0bm.v 總共有 98 行，比起同樣功能的流程式設計 mcu0m.v 的 51 行多了將近一倍，而且程式的設計難度感覺高了不少，但是我們可以很清楚的掌握到整個設計的硬體結構，這是採用流程式設計所難以確定的。
當然、由於筆者是「程式人員」，並非硬體設計人員，因此比較喜歡採用流程式的設計方式。不過採用了區塊式設計法設計出 mcu0bm.v 之後，也逐漸開始能理解這種「硬體導向」的設計方式，這大概是我在撰寫本程式時最大的收穫了。
雜誌訊息
讀者訂閱
程式人雜誌是一個結合「開放原始碼與公益捐款活動」的雜誌，簡稱「開放公益雜誌」。開放公益雜誌本著「讀書做善事、寫書做公益」的精神，我們非常歡迎程式人認養專欄、或者捐出您的網誌，如果您願意成為本雜誌的專欄作家，請加入 程式人雜誌社團 一同共襄盛舉。
我們透過發行這本雜誌，希望讓大家可以讀到想讀的書，學到想學的技術，同時也讓寫作的朋友的作品能產生良好價值 – 那就是讓讀者根據雜誌的價值捐款給慈善團體。 讀雜誌做公益也不需要有壓力，您不需要每讀一本就急著去捐款，您可以讀了十本再捐，或者使用固定的月捐款方式，當成是雜誌訂閱費，或者是季捐款、一年捐一次等都 OK ! 甚至是單純當個讀者我們也都很歡迎！
本雜誌每期參考價：NT 50 元，如果您喜歡本雜誌，請將書款捐贈公益團體。例如可捐贈給「羅慧夫顱顏基金會 彰化銀行(009) 帳號：5234-01-41778-800」。(若匯款要加註可用「程式人雜誌」五個字)
投稿須知
給專欄寫作者： 做公益不需要有壓力。如果您願意撰寫專欄，您可以輕鬆的寫，如果當月的稿件出不來，我們會安排其他稿件上場。
給網誌捐贈者： 如果您沒時間寫專欄或投稿，沒關係，只要將您的網誌以 [創作共用的「姓名標示、非商業性、相同方式分享」授權] 並通知我們，我們會自動從中選取需要的文章進行編輯，放入適當的雜誌當中出刊。
給文章投稿者： 程式人雜誌非常歡迎您加入作者的行列，如果您想撰寫任何文章或投稿，請用 markdown 或 LibreOffice 編輯好您的稿件，並於每個月 25 日前投稿到程式人雜誌社團 的檔案區，我們會盡可能將稿件編入隔月1號出版程式人雜誌當中，也歡迎您到社團中與我們一同討論。
如果您要投稿給程式人雜誌，我們最希望的格式是採用 markdown 的格式撰寫，然後將所有檔按壓縮為 zip 上傳到社團檔案區給我們， 如您想學習 markdown 的撰寫出版方式，可以參考 看影片學 markdown 編輯出版流程 一文。
如果您無法採用 markdown 的方式撰寫，也可以直接給我們您的稿件，像是 MS. Word 的 doc 檔或 LibreOffice 的 odt 檔都可以，我們 會將這些稿件改寫為 markdown 之後編入雜誌當中。
參與編輯
您也可以擔任程式人雜誌的編輯，甚至創造一個全新的公益雜誌，我們誠摯的邀請您加入「開放公益出版」的行列，如果您想擔任編輯或創造新雜誌，也歡迎到 程式人雜誌社團 來與我們討論相關事宜。
公益資訊
| 公益團體 | 聯絡資訊 | 服務對象 | 捐款帳號 |
|---|---|---|---|
| 財團法人羅慧夫顱顏基金會 | http://www.nncf.org/ 02-27190408分機 232 |
顱顏患者 (如唇顎裂、小耳症或其他罕見顱顏缺陷） | 銀行：009彰化銀行民生分行 帳號：5234-01-41778-800 |
| 社團法人台灣省兒童少年成長協會 | http://www.cyga.org/ 04-23058005 |
單親、隔代教養.弱勢及一般家庭之兒童青少年 | 銀行：新光銀行 戶名：台灣省兒童少年成長協會 帳號：103-0912-10-000212-0 |