對數 (logarithm) (作者：Bridan)
以前曾經寫文說明 開根號 的數學計算，今天就說明工程計算機另一重要計算功能 ─ 對數 。
對數的發明，是因為數學家想簡化算數乘除計算的繁瑣，對數的方法於1614年被約翰·納皮爾 (John Napier) 在 Mirifici Logarithmorum Canonis Descriptio (Description of the Wonderful Rule of Logarithms) 書中首次公開，而對數符號 log 來自拉丁文 logarithm，是由義大利數學家卡瓦列里 (Cavalieri，1598 - 1647) 所提出。
對數的觀念簡單的說，把數值乘除轉換成數值加減，在計算機發明前需要查表換算，加減計算後再反查表求出最後答案，因此有人發明 計算尺 ，解決查表換算問題。
log(X*Y) = log(X) + log(Y)
log(X/Y) = log(X) - log(Y)
log(Xa) = a * log(X)另外，為了區別以 10 為基底及 超越數 e (Euler's number) 為基底的對數，數學習慣分別表示為 log(X)和 ln(X)，而計算機語言喜歡用 log10(X)及 log(X)表示。在日常應用方面，由於人類對外界感覺的魯鈍，也運用了許多對數的觀念，例如，聲音用分貝、地震用芮氏規模、天文觀測用星等，意思是訊號要變化很大，人們才會有所感覺。
回歸主題，本文的要點為計算機如何計算對數值？在 資料型態認識─浮點數 (single ＆ double) 一文提到，任何正實數可以表示為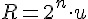 
， 是整數， 
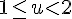，那
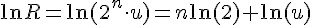
接下來就要思考如何計算 ln(u)，這需要 從等比級數和說起，令 Y 為等比級數和，將它減掉與 x 相乘的值等於 1，因此 Y 可得一個生成函數 1/(1-x)。
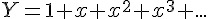
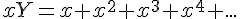
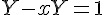
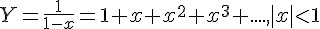
如果要讓等比級數和 Y 收斂等於生成函數，其要件為 |x|＜1。然後將 Y 對 x 積分可得，
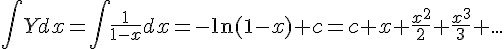
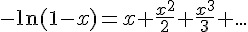
將上式 x 改以 -x 代入
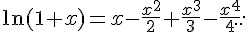
然後兩式合併
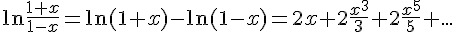
可能有人看到這裡，覺得越搞越複雜，其實這是計算機快速收斂最好的方法，因為計算 ln(1+x)將需要計算更多項次才能達到更好的精確度， 如果要精確到小數第 n 位，必須算到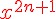 
。那如何求出 x，令
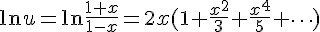
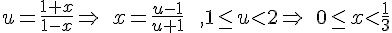
以上是超越數 e 為基底的對數計算，若想計算以 10 為基底的對數可以利用下列公式換算
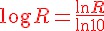
(本文來自「研發養成所」 Bridan 的網誌，原文網址為 http://4rdp.blogspot.tw/2014/06/logarithm.html ，由陳鍾誠編輯後納入程式人雜誌)