Nand2Tetris 第 7 週 -- VM I: Stack Arithmetic

在 Part I 第 6 週的時候，我們已經設計了 HackCPU 的組譯器，文章網址如下:

• 少年科技人雜誌 / 2015年6月號 : Nand2Tetris 第 6 週 -- 組譯器

如果您想要看看完整的組譯器程式碼，可以參考 github 中 havavha 同學的解答。

• https://github.com/havivha/Nand2Tetris/tree/master/06

當您寫完組譯器之後，其實要做出第 7 週的虛擬機就不會太困難了。

Nand2tetris 的課程就是安排得很巧妙，讓您循著階梯一步一步的向上爬，直到設計出整台電腦的軟硬體為止。

虛擬機

為甚麼要有虛擬機呢?

關於這個問題，主要是因為現實世界的處理器種類太多，因此如果我們想將 n 種程式語言直接轉換成 m 種處理器的機器碼，那麼就需要寫 n*m 個程式。

舉例而言，如果要將 10 種程式語言轉換成 10 種處理器的機器碼，那就得寫 10*10=100 個編譯程式，這樣實在有點困擾。

如果我們先將這些程式語言轉換成虛擬機的中間碼 (Intermediate Representation , IR)，然後再寫程式將中間碼轉換成組合語言或機器碼，那麼就只需要 n+m = 10+10 = 20 個程式，這對程式開發而言，是一個比較省力的策略。

以下是 Nand2Tetris 虛擬機的中間碼範例，您可以看到最右邊是真正的虛擬機碼？而最左邊是一個類似 java 的高階語言，稱為 JACK。

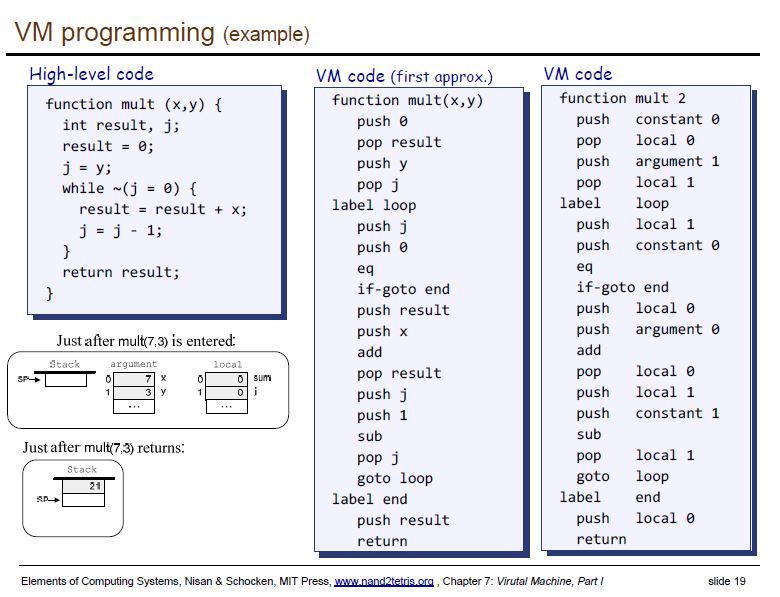
本圖來自 http://nand2tetris.org/course.php 第七章的投影片

而這兩週的習題，就是要我們實作一個可以將上述虛擬機的程式碼轉換成 HackCPU 組合語言的轉換程式。

第七週撰寫的轉換程式，主要處理的是基本運算的部分，而關於函數呼叫的轉換程式，則是第八週的習題。

轉換的方法

Nand2tetris 裏的虛擬機是堆疊式虛擬機，或稱堆疊機，所有需要進行加減乘除等運算的元素，都要被推入堆疊之後才能進行計算。

計算時會從堆疊中取出資料，計算完之後又會將結果推回堆疊裡面，以便下次計算時使用。

舉例而言，習題第 1 題就是要求我們寫程式將一個簡單的加法計算轉換為組合語言。

第 1 題: SimpleAdd.vm 轉為 SimpleAdd.asm

輸入: SimpleAdd.vm

push constant 7
push constant 8
add

但是、 HackCPU 並不是堆疊機，而且組合語言還長得頗為奇怪，因此我們要將上述指令轉為 HackCPU 的組合語言就必須先創造一個堆疊架構。

在前一章的組合語言中，其實已經保留了幾個特殊的組合語言符號，預留虛擬機使用，如下所示:

於是我們就可以利用上述的 SP 作為堆疊指標，以便進行堆疊推入與彈出的動作。

在虛擬機一開始時，會將堆疊指標 SP 先設好，在 nand2tetris 專案中通常會設在 256 的地方，也就是 M[0] = 256

例如 push constant 7 就可以轉換為

// push constant 7
@7          // A=7              
D=A         // D=7
@SP         // A=0
A=M         // A=M[0] ; 將 A 設定為 M[0]，也就是 256
M=D         // M[A] = M[256] = D = 7 ; 於是 M[256] 位置的內容變成 7 ，達成了將 7 推入堆疊的工作。
@SP         // A=0 
M=M+1       // M[A]=M[0]; M[0]=M[0]+1 於是將堆疊指標進到下一格，這樣下次推入時才不會把 7 蓋掉，真正完成推入動作。

同樣的，如果是 push constant 8 這個指令，相信您也知道怎麼編碼了。

雖然 SP 代表的是 0，但是當我們用來做堆疊指標時，其實通常用的是 M[0] 的內容，一開始設定為 256，堆疊的範圍位於 RAM[256 ... 2047] 之間。

為了避免混淆，我們用 SP 代表 0，然後用 *SP 代表 M[0] 的內容 (也就是堆疊頂端的位址)。

接著要編 add 的碼，請仔細看看對應的組合語言如下:

// add
@SP
M=M-1      // *SP=*SP-1
@SP
A=M        // A=M[0]=*SP
D=M        // D=M[A]=M[*SP] => 第一個取出的元素，用 P1 代表。
@SP        
M=M-1      // *SP=*SP-1      
@SP
A=M        // A=M[0]=*SP
A=M        // A=M[A]=M[*SP] => 第二個取出的元素，用 P2 代表。
D=D+A      // D = D + A = P1 + P2
@SP
A=M        // A=M[0]=*SP
M=D        // M[*SP] = D = P1 + P2 => 將加法的結果 P1+P2 推回堆疊中
@SP
M=M+1      // *SP=*SP+1

第 2 題: StackTest.vm 轉為StackTest.asm

輸入: StackTest.vm

// Executes a sequence of arithmetic and logical operations
// on the stack. 
push constant 17
push constant 17
eq
push constant 17
push constant 16
eq
push constant 16
push constant 17
eq
push constant 892
push constant 891
lt
push constant 891
push constant 892
lt
push constant 891
push constant 891
lt
push constant 32767
push constant 32766
gt
push constant 32766
push constant 32767
gt
push constant 32766
push constant 32766
gt
push constant 57
push constant 31
push constant 53
add
push constant 112
sub
neg
and
push constant 82
or
not

由於上一題中我們已經解說過 push constant 與 add 的運算的組合語言，所以接下來我們只說明 and, or, not, sub, gt, eq 等指令的作法。

sub 指令和 add 很像，只不過 D=D+A 改為 D=D-A 而已。同樣的， and 指令與 add 指令也只差在將 D=D+A 改為 D=D&A 而已， or 指令則是改用 D=D|A。

接著、讓我們看看單參數的運算，像是 neg 與 not 是如何翻譯為組合語言的，以下是 neg 的例子：

// neg
@SP
M=M-1      // *SP=*SP-1
@SP
A=M        // A=M[0]=*SP
D=M        // D=M[A]=M[*SP] => 第一個取出的元素，用 P1 代表。
D=-D       // D= -D = -P1
@SP
A=M        // A=M[0]=*SP
M=D        // M[*SP] = D = -P1
@SP        
M=M+1      // *SP=*SP+1

仔細看上面的註解，您應開可以理解這種奇特組合語言的思路邏輯。

如果換成 not 運算，只不過是將上面的 D=-D 改為 D=!D 而已。

最後我們來看看像 gt 這樣的運算，其對應的組合語言如下所示:

// gt
@SP
M=M-1      // *SP = *SP-1
@SP
A=M        // A=M[0]=*SP
D=M        // D=M[A]=M[*SP] => 第一個取出的元素，用 P1 代表。
@SP
M=M-1      // *SP = *SP-1
@SP        // A=M[0]=*SP
A=M
A=M        // A=M[A]=M[*SP] => 第二個取出的元素，用 P2 代表。
D=A-D      // D = A-D = P2-P1
@LABEL17   
D;JGT      // if (P2-P1 > 0) goto LABEL17
@SP        
A=M        // A=M[0]=*SP
M=0        // M[*SP] = 0  ; 當 P1<=P2 時將 0 推入堆疊。 在 nand2tetris 的 JACK 語言中，用 0 代表 false
@LABEL18
0;JMP      // goto LABEL18
(LABEL17)
@SP
A=M        // A=M[0]=*SP
M=-1       // M[*SP] = -1 ; 當 P1>P2 時將 -1 推入堆疊。 在 nand2tetris 的 JACK 語言中，用 -1 代表 true
(LABEL18)
@SP
M=M+1      // *SP = *SP+1

第 3 題: BasicTest.vm 轉為 BasicTest.asm

接下來，在第 3 題的 BasicTest.vm 中，我們要處理更多類型的 push 與 pop 動作，像是 push local, push argument, pop this, ....

以下是習題的內容。

輸入: BasicTest.vm

// Executes pop & push commands using the virtual memory segments.
push constant 10
pop local 0
push constant 21
push constant 22
pop argument 2
pop argument 1
push constant 36
pop this 6
push constant 42
push constant 45
pop that 5
pop that 2
push constant 510
pop temp 6
push local 0
push that 5
add
push argument 1
sub
push this 6
push this 6
add
sub
push temp 6
add

要做這題習題的程式之前，請務必先看過下列的 HackComputer 的記憶體配置地圖。

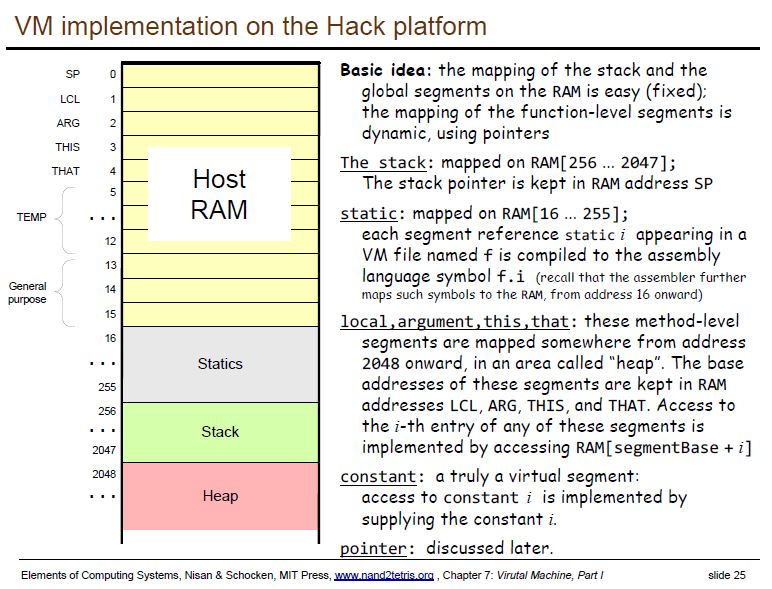
本圖來自 http://nand2tetris.org/course.php 第七章投影片

還有要清楚組譯器中各個分段符號的名稱代號的意義，如下圖所示。

本圖來自 http://nand2tetris.org/course.php 第六章投影片

理解了上述配置之後，就可以開始進行組合語言的翻譯了。

先讓我們看看 push argument 與 pop argument 的翻譯法，請記得 ARG 符號對應的記憶體位址為 RAM[2]，我們用 *ARG 來代表 RAM[2] 的內容。

// push argument 1
@1
D=A         // D = 1
@ARG
A=M         // A = M[2] = *ARG
AD=D+A      // A = D = 1+M[2] = 1+*ARG
D=M         // D = M[A] = M[1+*ARG]
@SP
A=M         // A = M[0] = *SP
M=D         // M[*SP] = D = M[1+*ARG]  ; 將 ARG[1] 推入堆疊中
@SP
M=M+1       // *SP = *SP+1

// pop argument 2
@SP
M=M-1       // *SP = *SP-1
@2
D=A         // D=2
@ARG
A=M         // A=M[2]=*ARG
AD=D+A      // A=D=2+*ARG
@R15
M=D         // M[15] = D = 2+*ARG
@SP
A=M         // A=M[0]=*SP
D=M         // D=M[A]=M[*SP] ; 取得堆疊資料 pop1
@R15
A=M         // A = M[15] = 2+*ARG
M=D         // M[A] = M[2+*ARG] = D = pop1

與 argument 的存取相類似的，push local 與 pop local 等運算也是利用同樣的方式，只不過將 ARG (M2) 改為 LCL (M1) 而已。

同樣的 ， push this, pop this, push that, pop that 也都是依照相同的方式，這些不同型態的堆疊存取法會對應到高階語言 JACK 的區域變數 (local, LCL)， 參數 (argument, ARG)， 物件變數 (this) 與陣列 (that, 命名有點怪 ....) 。

另外還有 temp, pointer, static 等全域變數，分別對應到 temp (5~12), static (16~255), pointer (3~4) (3 代表 this, 4 代表 that)。

接著在第四題我們就要處理 pointer 的推入與取出，如此才能在正確設定 this, that 的分段位址之後，繼續用 push this, pop this, push that, pop that 進行物件與陣列的處理。

第 4 題: PointerTest.vm 轉為 PointerTest.asm

輸入: PointerTest.vm

push constant 3030
pop pointer 0
push constant 3040
pop pointer 1
push constant 32
pop this 2
push constant 46
pop that 6
push pointer 0
push pointer 1
add
push this 2
sub
push that 6
add

請記得 POINTER 區段位於 RAM[3~4]，其中 RAM[3] 為 this ， RAM[4] 為 that。

// push pointer 1
@R4     // POINTER[1] = 3+1 = 4
D=M     // D = M[4] = POINTER[1]
@SP
A=M     // A=M[0]=*SP
M=D     // M[*SP]=POINTER[1]
@SP
M=M+1   // *SP = *SP+1

// pop pointer 1
@SP
M=M-1   // *SP = *SP-1
@SP
A=M     // A = M[0] = *SP
D=M     // D = M[*SP] = 堆疊取出的內容
@R4
M=D     // M[4]=POINTER[1]=D=堆疊取出的內容

第 5 題: StaticTest.vm 轉為 StaticTest.asm

接著是 static 變數的處理，請記得 static 變數位於 RAM[16..255] 區段中。

輸入: StaticTest.vm

push constant 111
push constant 333
push constant 888
pop static 8
pop static 3
pop static 1
push static 3
push static 1
sub
push static 8
add

其中 push static 8 與 pop static 8 轉換為組合語言後如下所示。

// push static 8
@StaticTest.8 // 組譯器會自動安排 StaticTest.8 的位址
D=M           // D = *StaticTest.8
@SP
A=M           // A = M[0] = *SP
M=D           // M[*SP] = D = *StaticTest.8 ; 推入 static 變數到堆疊中。
@SP
M=M+1         // *SP = *SP+1

// pop static 8
@SP
M=M-1         // *SP = *SP - 1
@SP
A=M           // A = M[0] = *SP
D=M           // D = M[*SP] ; 從堆疊取出的內容
@StaticTest.8 // 組譯器會自動安排 StaticTest.8 的位址
M=D           // *StaticTest.8 = 從堆疊取出的內容

有時，當筆者想不出來時，還是會看一下 havavha 同學的解答，例如他對 static 型態變數的處理如下，看完之後我再回去繼續用 javascript 與 node.js 寫自己的程式，通常就可以順利寫出了。

有 havavha 同學的幫助，真好!

    def _static_to_stack(self, seg, index):
        self._a_command(self._static_name(index))   # A=&func.#
        self._c_command('D', 'M')                   # D=func.#
        self._comp_to_stack('D')                    # *SP=func.#

...

   def _stack_to_static(self, seg, index):
        self._stack_to_dest('D')
        self._a_command(self._static_name(index))
        self._c_command('M', 'D')

結語

雖然要寫出這個程式並不算太容易，但對筆者而言，理解 HackCPU 的組合語言這部分，才是最困難的。

一旦寫出每個中間指令對應的機器碼之後，程式自然就迎刃而解了!