金融短訊:SHA 安全雜湊算法
由於上文介紹「比特幣」時發現「安全雜湊算法家族 SHA」 是該系統的一個關鍵演算法,目前的比特幣採用 SHA-2 (SHA-224、SHA-256、SHA-384,和SHA-512 的統稱, 比特幣應該是採用 SHA-256) 的演算法,因此我們將在此介紹有關 SHA 算法家族的原理,以便能進一步理解「比特幣」的運作原理。
簡介
安全雜湊演算法(英語:Secure Hash Algorithm)是一種能計算出一個數位訊息所對應到的,長度固定的字串(又稱訊息摘要)的演算法。且若輸入的訊息不同,它們對應到不同字串的機率很高;而SHA是FIPS所認證的五種安全雜湊演算法。這些演算法之所以稱作「安全」是基於以下兩點(根據官方標準的描述):「1)由訊息摘要反推原輸入訊息,從計算理論上來說是很困難的。2)想要找到兩組不同的訊息對應到相同的訊息摘要,從計算理論上來說也是很困難的。任何對輸入訊息的變動,都有很高的機率導致其產生的訊息摘要迥異。」
SHA家族的五個演算法,分別是SHA-1、SHA-224、SHA-256、SHA-384,和SHA-512,由美國國家安全域(NSA)所設計,並由美國國家標準與技術研究院(NIST)發佈;是美國的政府標準。後四者有時並稱為SHA-2。SHA-1在許多安全協定中廣為使用,包括TLS和SSL、PGP、SSH、S/MIME和IPsec,曾被視為是MD5(更早之前被廣為使用的雜湊函式)的後繼者。但SHA-1的安全性如今被密碼學家嚴重質疑;雖然至今尚未出現對SHA-2有效的攻擊,它的演算法跟SHA-1基本上仍然相似;因此有些人開始發展其他替代的雜湊演算法。緣於最近對SHA-1的種種攻擊發表,「美國國家標準與技術研究院(NIST)開始設法經由公開競爭管道(類似高級加密標準AES的發展經過),發展一個或多個新的雜湊演算法。」
2012年10月2號,Keccak被選為NIST雜湊函式競賽的勝利者,成為SHA-3。 SHA-3並不是要取代SHA-2,因為SHA-2目前並沒有出現明顯的弱點。由於對MD5出現成功的破解,以及對SHA-0和SHA-1出現理論上破解的方法,NIST感覺需要一個與之前演算法不同的,可替換的加密雜湊演算法,也就是現在的SHA-3。設計者宣稱在Intel Core 2的CPU上面,此演算法的效能是12.5cpb(每位元組周期數,cycles per byte)。不過,在硬體實做上面,這個演算法比起其他演算法明顯的快上很多。
SHA-0 和 SHA-1可將一個最大 2 的 64 次方位元的訊息,轉換成一串160位元的訊息摘要;其設計原理相似於MIT教授Ronald L. Rivest所設計的密碼學雜湊演算法 MD4 和 MD5。
安全雜湊算法 SHA 家族的「輸入、輸出、迴圈次數、與目前的安全性」等特性,可參考以下列表。
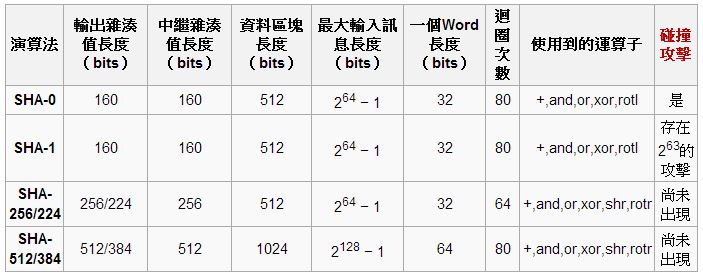
圖、雜湊算法 SHA 家族的特性表
SHA-1 的演算法
以下是 SHA-1 演算法其中一個步驟的示意圖:
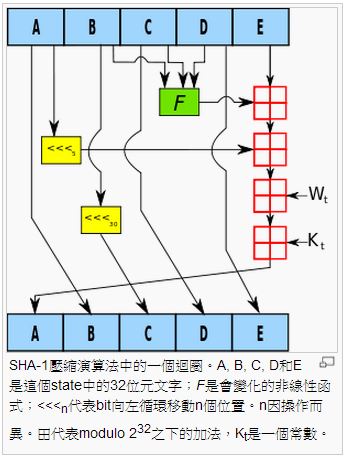
圖、SHA-1 演算法的一個步驟
完整的 SHA-1 演算法如下所示:
// Note: All variables are unsigned 32 bits and wrap modulo 2^32 when calculating
// 注意:所有變數都是 32 位元的無號整數,而且計算時都會對 2^32 取餘數。
// Initialize variables: 初始化下列變數
h0 := 0x67452301
h1 := 0xEFCDAB89
h2 := 0x98BADCFE
h3 := 0x10325476
h4 := 0xC3D2E1F0
// Pre-processing: 前處理階段
append the bit '1' to the message (對訊息補上一個 1)
append k bits '0', where k is the minimum number >= 0 such that the resulting message
length (in bits) is congruent to 448(mod 512) (若訊息長度未達 448 mod 512,則補一堆 0)
append length of message (before pre-processing), in bits, as 64-bit big-endian integer (
// Process the message in successive 512-bit chunks:
break message into 512-bit chunks
for each chunk
break chunk into sixteen 32-bit big-endian words w[i], 0 ≤ i ≤ 15
// Extend the sixteen 32-bit words into eighty 32-bit words:
for i from 16 to 79
w[i] := (w[i-3] xor w[i-8] xor w[i-14] xor w[i-16]) leftrotate 1
// Initialize hash value for this chunk:
a := h0
b := h1
c := h2
d := h3
e := h4
// Main loop:
for i from 0 to 79
if 0 ≤ i ≤ 19 then
f := (b and c) or ((not b) and d)
k := 0x5A827999
else if 20 ≤ i ≤ 39
f := b xor c xor d
k := 0x6ED9EBA1
else if 40 ≤ i ≤ 59
f := (b and c) or (b and d) or(c and d)
k := 0x8F1BBCDC
else if 60 ≤ i ≤ 79
f := b xor c xor d
k := 0xCA62C1D6
temp := (a leftrotate 5) + f + e + k + w[i]
e := d
d := c
c := b leftrotate 30
b := a
a := temp
// Add this chunk's hash to result so far:
h0 := h0 + a
h1 := h1 + b
h2 := h2 + c
h3 := h3 + d
h4 := h4 + e
// Produce the final hash value (big-endian):
digest = hash = h0 append h1 append h2 append h3 append h4SHA-1 的編碼範例
以下幾個範例顯示了 SHA-1 的用法:
範例一:SHA-1 的編碼範例
SHA1("The quick brown fox jumps over the lazy dog")
16進位:2fd4e1c6 7a2d28fc ed849ee1 bb76e739 1b93eb12
Base64:L9ThxnotKPzthJ7hu3bnORuT6xI=範例二:範例一中的 dog 改為 cog 之後,SHA-1 的編碼結果就完全不同了。(而這也正式難以破解的原因,無跡可尋啊!)
SHA1("The quick brown fox jumps over the lazy cog")
16進位:de9f2c7f d25e1b3a fad3e85a 0bd17d9b 100db4b3
Base64:3p8sf9JeGzr60+haC9F9mxANtLM=範例三:空字串的 SHA-1 編碼結果
SHA1("")
16進位:da39a3ee 5e6b4b0d 3255bfef 95601890 afd80709
Base64:2jmj7l5rSw0yVb/vlWAYkK/YBwk=如果您對「如何用 SHA-1 實作雜湊現金技術」有興趣,可以參考筆者的另一篇文章,連結如下:
結語
雖然 SHA-1 已經在各種資訊安全協定中廣被採用,但還是有些弱點,這也是為何要開發 SHA-2 與 SHA-3 的原因。
2005年,Rijmen 和 Oswald 發表了對 SHA-1 較弱版本(53次的加密迴圈而非80次)的攻擊:在 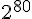 的計算複雜度之內找到碰撞。
的計算複雜度之內找到碰撞。
2005年二月,王小雲、殷益群及於紅波發表了對完整版SHA-1的攻擊,只需少於 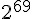 的計算複雜度,就能找到一組碰撞。
的計算複雜度,就能找到一組碰撞。
2005年8月17日的 CRYPTO 會議尾聲中王小雲、姚期智、姚儲楓再度發表更有效率的SHA-1攻擊法,能在 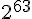 個計算複雜度內找到碰撞。
個計算複雜度內找到碰撞。
2006年的 CRYPTO 會議上,Christian Rechberger和Christophe DeCannière 宣布他們能在容許攻擊者決定部分原訊息的條件之下,找到SHA-1的一個碰撞。
不過這些攻擊法其實還是需要 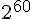 以上的複雜度,而比特幣所採用的 SHA-2 到目前為止還沒有被較快速破解成功的案例, 但是還是有人認為 SHA-2 其實並不夠安全,像是以下文章就有這方面的質疑。
以上的複雜度,而比特幣所採用的 SHA-2 到目前為止還沒有被較快速破解成功的案例, 但是還是有人認為 SHA-2 其實並不夠安全,像是以下文章就有這方面的質疑。
隨著技術進步,加密法似乎總是必須更新以防止破解的,不過類似比特幣這樣的系統,是相當有啟發性且創新的一種做法, 資訊領域的技術進入金融世界之後,或許還能摩擦出更多的火花也說不定。
參考文獻
- 維基百科:SHA家族
- Wikipedia:SHA-1
- rfc3174: US Secure Hash Algorithm 1 (SHA1)
- 資訊與網路安全技術
- 5-8 SHA-1 (Secure Hash Algorithm) 演算法
- 5-6 MD5 壓縮函數
【本文由陳鍾誠取材並修改自 維基百科,採用創作共用的 姓名標示、相同方式分享 授權】