亂數產生器 (作者:Bridan)
想過電腦中亂數產生器如何設計的嗎?
大多數亂數產生器採用 線性同餘法 設計 ( Linear Congruential Generator, LCG ),因為方法簡單以及亂數 均勻分佈 ( Uniform distribution )。
其原理為:
Xn = a Xn-1 + b 將一正整數乘以 a 常數再加上 b 常數,
0<= Xn<M 除 M 取餘數,這個 Xn 可重複代入上式計算下一個亂數。各位可以參考 EXCEL 檔 ,我選用 a = 49,b = 0,M = 215 = 32768,C 欄位就是亂數,介於零與一之間,從 E、F 欄位可以看出數值分部非常均勻。 另外,從 A 欄位會發現,每 2048 筆資料會重複循環,這裡所舉的例子是方便讀者明瞭原理,商用軟體至少用32 bits,並挑選合適的 a b 值,所以很難發現重複性。
通常均勻分佈的亂數產生器就夠用,不過與統計有關的程式還需要 常態分佈 ( Normal distribution ) 的亂數產生器,那如何設計呢?還記得 中央極限定理 ( Central limit theorem ) 吧!從未知分佈的母群體中抽樣,只要能計算出這群體平均數 μ 以及有限的變異數 σ2,那麼抽出 n 個隨機樣本取平均值,當 n 趨近無窮大,它的平均值抽樣分配將近似於常態分佈。再以 EXCEL 檔內容為例,一般程式計算時間有限不可能無窮計算下去,因此 只取連續六筆資料平均再正規化 ,原均勻分佈的 C 欄位值,經過計算後就成為 H 欄位常態分佈的亂數,請參考 J 欄位的機率分佈。
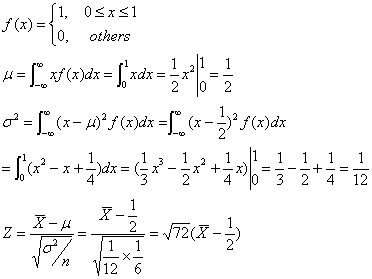
另外,常態分佈亂數方法二,請參考 http://4rdp.blogspot.com/2008/06/random-variable-of-normal-distribution.html 。
(本文來自「研發養成所」 Bridan 的網誌,原文網址為 http://4rdp.blogspot.tw/2008/06/blog-post_14.html ,由陳鍾誠編輯後納入程式人雜誌)